1. 引言
数控加工产品质量和成本的控制与数控加工设备的参数设置具有直接关系。在建立加工参数模型后,对模型的参数进行优化,并结合相关的优化算法来寻找最优的加工参数,这种方法是目前最高效的加工参数选择方法 [1] [2] 。从基于算法的加工优化方法发展来看,多目标优化是加工参数优化方案的最佳选择。目前,数控加工领域广泛应用的多目标优化算法有两种:一是,利用线性加权法将多目标分解为多个单一的模型,从而寻找各个目标的最优参数 [3] ;二是在遗传算法中加入Pareto概念,通过这两者的结合来寻求最优加工参数 [4] ,还有与智能算法结合,例如粒子群算法和模糊综合评判法得到多目标优化最优解 [5] 。线性加权和法和权重系数法尽管可以得到最优化的结果,但因为设计者对优化模型的了解程度、有限的优化经验及个人喜好等因素的影响,难以确定合适的目标函数的权重系数,所以得到的优化解往往受限于一定的条件;而基于Pareto遗传算法得到的往往是最优解集,从中合理决策出最优解是当前主要解决的热点问题,并且其在高维决策空间中收敛性能不佳。
针对此问题,出现了基于基因表达式编程的多目标优化算法 [6] ,但目前还停留在理论阶段;还有通过仿真及与其他智能算法相结合,2015年,范超等将Pareto与蚁群算法相结合,获得Pareto沿后,根据拥挤距离来剔除解集中的解,具有一定的主观性 [7] ;周志恒等利用层次分析法对Pareto前沿解进行决策,得到最优加工参数组合,也主要是利用决策者的经验,判断并给出每个决策方案的标准的权数,也带有一定的主观性 [8] ;2016年,邓涛等通过仿真得到Pareto解集,但仍然没有解决最优解决策问题 [9] 。从Pareto最优解集中决策出最优解仍是当前Pareto遗传算法应用于数控加工参数优化迫切需要解决的问题。本文将Pareto遗传算法与TRIZ理论相结合,基于TRIZ发明问题解决理论,对Pareto最优解集中的参数进行分析,归纳总结参数间的技术矛盾,运用技术矛盾解决原理去进行合理选择和决策,实现真正意义上的先优化后决策的多目标优化。
2. 改进型Pareto遗传算法
遗传算法模拟自然环境下的生物遗传和进化过程,在此基础上建立高度并行、随机和自适应形式的通用优化算法,也是最常用的智能优化算法 [10] 。基于数控加工非线性特点及多目标优化需求,本文采用Pareto遗传算法与MATLAB工具箱进行结合的方式,得到Pareto最优解集,并且将Pareto概念与遗传算法相结合求最优解是目前基于遗传算法的多目标优化问题的最常用方法之一 [11] 。
TRIZ能够有效解决产品创新中遇到的问题,解决矛盾和冲突是产品创新的核心 [12] ,科学运用RIZ理论中的矛盾解决策略能够有效消除产品创新过程中出现的技术冲突和物理冲突。TRIZ理论提出了39个工程参数的抽象描述方法,而且这些描述方法能够有效解释对象冲突的本质,TRIZ理论还提出了39个通用的工程参数,构建了用于分析参数问题的冲突矩阵模型,其中“列”所描述的是需要改善的一方,而“行”所针对的则是恶化的一方,而后基于一定的规则,将40条发明原理视为参考解列入其中,从而得到冲突解决原理表。在实际应用过程中,为了促使问题实现抽象化,还需要借助参数来进行定义描述,并在矩阵表中确定对应的原理号 [13] ,根据解决原理号及原理内容,结合实际,分析、提炼和总结,最终找到解决问题的方法。TRIZ理论的39个通用工程参数及其40条发明原理是针对所有问题基础上的提炼和通用,从而保证了应用的科学性。
根据上述理论分析,结合TRIZ理论功能特点,将Pareto遗传算法和TRIZ理论进行有机结合,从而得到改进型Pareto遗传算法。分析Pareto最优解集中加工参数间的关系,确定其之间的矛盾关系,基于TRIZ理论定义成技术矛盾,形成具体问题并用TRIZ的标准用语进行概括,进而形成TRIZ的标准问题,然后在矛盾矩阵表对应寻找问题解决原理,再结合实际加工条件合理选择和决策加工参数,避免了根据经验在Pareto解集中确定最优解的主观性,实现了具有科学依据的客观性决策,从而构建和完善先寻优后决策的求解方法。具体过程如图1所示。
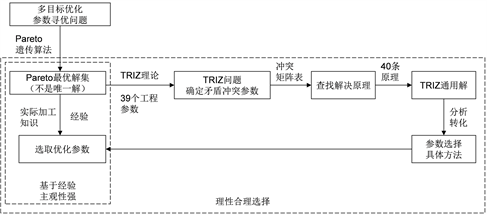
Figure 1. Improved Pareto genetic algorithm flow chart
图1. 改进型Pareto遗传算法运算流程图
3. 建立数学模型
数控切削粗加工阶段,一般以高生产率为主,加工参数的选择也一般遵循保证最大生产效率和最低加工成本的原则,但往往也会受到机床和刀具性能及相关参数的限制和约束,因此,选择最优数控加工参数可以被看做为是一个受约束的多目标优化问题。
3.1. 设计变量
在明确机床刀具参数、机床参数和工件参数的情况下,进给量f、切削速度v、切削深度ap对生产效率的影响最大 [14] 。由于ap是取决于零件的切削余量,同时ap对刀具耐用度的影响不大,为此可将ap当作是常量。由此可得,待优化的设计变量为切削速度和进给量 [15] 。本文以螺旋铣削加工为例,其切削运动由两种进给运动合成,即刀具主轴的轴向进给运动和刀具的切向进给运动。因此,设计变量即待优化的参数为:切削速度
,每齿进给量
,其表达式为
。
3.2. 目标函数
优化切削参数的主要目的是为了实现对成本的控制和提高生产效率,但刀具磨损和失效对成本的影响最大。因此,选择切削效率、刀具耐用度和加工成本作为优化目标。
切削时间越少,则切削的效率就越高,切削效率
可表示为
(1)
式中
为切削时间,
;
为工件直径,
;
为切削速度,
;
为工件切削长度,
;
为每齿进给量,
;
为刀具齿数。
根据金属切削理论 [16] ,刀具耐用度
表示为
(2)
式中,
为耐用度系数,由工件材料、刀具材料和其他切削条件等确定;指数
、
、
分别表示
、
、
影响刀具耐用度的程度,其值需要通过实验或根据经验定性确定。
单件工序成本 = 加工费用 + 换刀费用 + 刀具使用成本 + 辅助费用,公式如下
(3)
式中,
为工序切削加工工时,
为单位时间内工序分摊的企业费用,
为一次换刀所需时间,
为刀具成本,
为除换刀以外的辅助时间。
3.3. 约束参数
在数控加工时,对切削用量产生影响的因素包括切削力、机床功率和表面精度等,这些因素形成了参数优化的约束条件。
常用的约束条件表示如下 [17] :
1) 主切削力约束
(4)
式中
为主切削力,
;
为最大主切削力允许值,
;系数
由被加工材料和切削条件决定;
、
、
为
、
、
的指数;加工设备和工具参数,以及加工实际条件与经验公式条件不匹配的情况下,切削力的修正系数为
。
2) 机床功率约束
(5)
式中,
为机床效率;
为机床最大功率,
。
3) 工件表面粗糙度约束
(6)
式中,
为刀尖圆弧半径,
;
为工件表面轮廓最大高度允许值,
。
4) 切削用量范围约束
大量的实践研究证明,刀具的工作寿命受切削速度的影响最大,每齿进给量次之,轴向切削深度对刀具寿命的影响作用最小。在加工铝合金产品时,只有提高切削扭矩,并保持较低的切削速度才能保证切削质量,正常情况下,切削速度小于100 r/min,螺旋铣刀的直径范围为6 mm~10 mm,因此机床主轴转速范围为2000 r/min~5000 r/min,每齿进给量的变化范围为0.1 mm/齿~0.3 mm/齿 [18] 。在进行螺旋铣削过程中,因为铣平面切削力较小 [19] ,因此在进行切削参数优化时,切削力及机床功率的约束条件可以被忽略,而以加工表面粗糙度为主要约束条件。
3.4. Pareto最优解集
以加工凸轮为例,如图2所示,所选用的数控机床为S56 MAKINO,零件材料为6061铝合金板料。
根据优化目标和约束条件,确定优化数学模型。目标函数为:
(7)
(8)
(9)
设计变量为:
,
约束条件为:切削速度
每齿进给量
表面粗糙度
由切削用量手册,可以得出刀具耐用度系数:Cz = 2118,α = 1.5,β = 0.5,γ = 0.5;根据上述分析,ap = 0.15 mm;选用螺旋铣刀参数:齿数Z = 4,刀具直径d = 6 mm;加工零件长度如图2所示凸轮外形轮廓周长L = 80 mm。根据工序切削加工工时
为2 min,单位时间内工序分摊的企业费用
为0.625元/min,一次换刀所需时间
为5 min,刀具成本
为200元,辅助时间
为30 min。借助MATLAB软件开展计算工作,其各项参数依次为:默认种群范围为60、更迭次数为200、交叉几率为0.8、变异几率为0.05,优化结果如图3和表1所示。
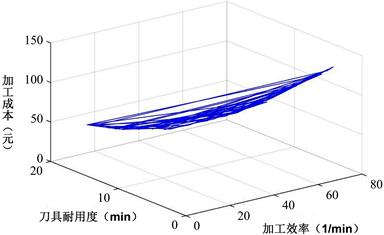
Figure 3. Pareto solution set of cam cutting parameters
图3. 凸轮切削参数Pareto解集

Table 1. Optimization results of cam
表1. 凸轮优化结果
原则上,最优解可以是图3中Pareto曲线上的任意点,此时,一般都是基于经验和偏好主观进行选择和决策,并且,在实际切削加工中一般会兼顾三个目标,尽量选择位于中部区域值的状态 [20] ,即选择加工效率 ≤ 40(min−1),刀具耐用度 ≤ 80(min),加工成本 ≤ 80元的参数,得到表2所示的三组参数,出于实验需求,可将三组数据转化成加工参数。但此种选择和决定最优解集的方式,主观性太强,科学依据缺乏,最重要的是得到的是最优解集,而不是最优解。

Table 2. Selected machining parameters based on experience of cam
表2. 基于经验选择的凸轮加工实验参数
4. 最优解决策
4.1. 确定矛盾
从图3和表1中不难发现,加工参数在变化范围上偏大,同时,在刀具耐用度为最大值情况下,加工效率及加工成本保持最低,当加工效率为最高值时,刀具耐用度值最小,而成本则处于最大值,即当刀具耐用度增加时,加工效率便降低,加工成本也降低。依据TRIZ理论中的39个工程参数,将这一原始问题描述为三个标准技术参数:第一个参数为“刀具耐用度”,第二个参数为“加工效率”,第三个参数为“加工成本”,假设“刀具耐用度”和“加工成本”为需改善参数,则“加工效率”为恶化参数;进而根据TRIZ理论39个通用工程参数,通过分析其含义,将“刀具耐用度”、“加工效率”和“加工成本”分别用“运动物体的作用时间”、“生产率”和“物质损失”表示 [21] ,保证了实际问题参数与TRIZ理论通用参数的一致性和合理性,再根据TRIZ理论矛盾定义,将其定义为技术矛盾。
4.2. 确定问题解决原理
表3是TRIZ理论的矛盾矩阵表 [22] ,根据“运动物体的作用时间”和“生产率”这一对技术矛盾参数,即“刀具耐用度”和“加工效率”这两个优化目标参数,找到相对应的解决原理为 14,17,19,35;根据“物质损失”和“生产率”这两个优化目标参数,找到相对应的解决原理为28,35,10,23;再从原理阐述的具体内容中分析和提炼出符合实际问题的有效原理,具体过程如图4所示。原理10:预先作用原理:预先安置物体,促使其处于最方便位置,从而促使运送时间得到有效的缩减;原理14:实施曲面化,采用辊、球和螺旋,诸如,螺旋齿轮能够保证承载能力的均匀性;在实施数控加工过程中,采用专用螺旋铣刀,使得刀具受力均匀,提高耐用度;原理17:维数变化,五轴机床的刀具可被定位到任意所需的位置上,提高加工效率;原理19:周期性作用,批量制造,同样也需要提高加工效率;原理23:反馈原理:在98系统中引入反馈,例如自动工艺控制,提高加工效率和质量;原理28:机械系统替代原理:用光学系统、声学系统等代替机械系统,提高效率和效能;原理35:参数变化,提供智能在线目录,智能制造,提高加工效率。
4.3. Pareto最优解的理性决策
根据图4分析结果,提高生产率重于提高刀具耐用度和降低加工成本,因此,在选择优化参数时,将每一组参数所对应的生产率、刀具耐用度和加工成本进行横向比较,以高生产率,兼顾较高刀具耐用度和较低的加工成本为根据进行决策和选择。针对本文表2中基于经验选择的三组凸轮加工参数Pareto最优解,根据TRIZ理论分析,通过比较,第29组参数满足要求,确定为最终最优加工参数,此时加工效率为32.707 min−1,刀具耐用度为7.624 min时,加工成本72.78元,切削速度为79.071 m/min,进给量为0.156 mm/齿。
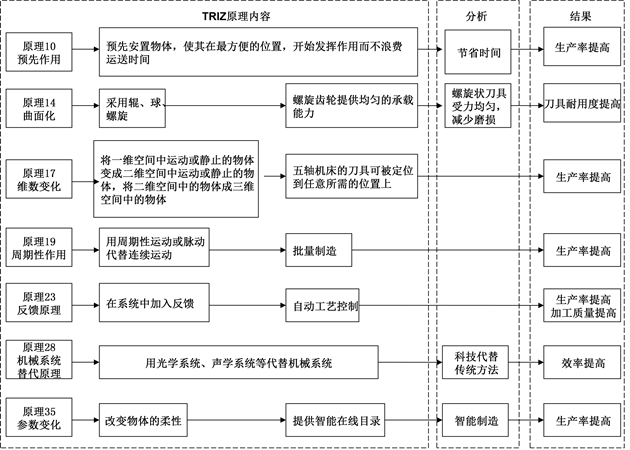
Figure 4. Analysis process based on TRIZ
图4. 基于TRIZ发明问题解决原理分析过程
5. 加工实验验证
基于上述研究,从表2中分别选择三组加工参数开展实验,通过加工时间和测量表面粗糙度,结合刀具耐用度及加工效率的综合评价对比三组参数的加工效果,得到和确定最优加工参数,进而验证改进型Pareto遗传算法的有效性,加工实验过程如图5所示。
借助数控编程,确定三组参数对零件进行切削加工,从而得到不同的加工效果,并采用粗糙度检测仪就表面粗糙度进行测量,获得不同的结果,如图6和表4所示,对应序号为29、45和46的加工参数,粗糙度值分别为:0.418 μm,0.345 μm,和0.483 μm,均达到加工要求。此外,通过实际加工时间与理论加工时间的对比,发现实际加工时间比理论加工时间要长,误差值范围在0.1 min~0.2 min,是由于实际加工路线与理论路线不同和测量误差所致。但显然,采用第29组参数进行加工时,加工效率较高,同时也具有较高的刀具耐用度和较低的加工成本,可以确定为最优加工参数,此实验结果与3.3理论分析结果一致。由此证明了本文提出的改进型Pareto遗传算法——Pareto遗传算法和TRIZ理论相结合方法的可行性与有效性。

Figure 6. Machined surface roughness values of three groups parameters of cam
图6. 三组不同加工参数凸轮表面粗糙度值

Table 4. Comparison between theoretical and actual measurement value of cam machining experiment
表4. 凸轮加工实验理论值与实际测量值比较
6. 结论
本文结合TRIZ理论,提出了一种先优化后理性决策的改进型Pareto遗传算法,并以铣削铝合金为例,以加工效率、刀具耐用度和加工成本为目标函数,以切削速度和进给量为设计变量建立数学模型,得到Pareto最优解集;再基于TRIZ理论总结的相应原理对最优解进行理性决策,确定最终最优加工参数。与传统Pareto遗传算法相比,改进型Pareto遗传算法避免了基于经验选择和决策最优解的主观性,为选择最优解提供了科学理论依据,完善了先优化后决策的多目标优化寻优模式。最后,通过凸轮加工实验,验证了方法的可行性,满足加工表面粗糙度要求的同时,使得加工参数达到最优,增加了刀具寿命,降低了加工成本,提高了加工效率。
参考文献
NOTES
*通讯作者。