1. 引言
随着计算机和数字化处理技术的快速发展,CAD技术在医学影像研究中越来越占据着重要地位,并已在医学诊断中充分展示出了其临床价值。通过计算机将影像学获得的数据导入医学图形图像处理软件,经过计算机的数值计算分析,帮助医师找出病灶,从而能够提高诊断的准确效率。Taubin在1995年提出了一种基于Laplacian流的网格信号处理方法 [1] ,有效地光顺曲面去掉其上的噪声。Desbrun等人采用隐式的Laplacian算子和平均曲率流方法来处理网格光顺去噪问题 [2] ,为了解决顶点漂移的问题,它将顶点的移动方向限制在法向方向,对于网格光顺达到了较好的效果。Pauly等人将广泛应用在网格光顺中的Laplacian算子应用到点模型上 [3] ,但由于点云模型由散乱点组成,使用该算法可能会出现特征被磨平的情况,同时如果一些点没有按照法向的方向移动,可能会引起顶点漂移的情况;Levent等 [4] 开发了一种基于笔式草绘的可变形曲线网造型系统,用户可以在选定的3D模板上用笔在单视图或任意视角的多视图中创建和修改曲线,所有曲线连接起来形成曲线网,但该系统的工作量都非常大。由杨 [5] 等人基于文献 [6] 提出的多尺度分析法是一种特征提取方法,该方法需要选择适当的尺度因子,再利用二阶离散曲率提取特征点,但是未能进行全尺度空间分析,同时二阶离散曲率法由于支撑区间太小,曲率计算受噪声影响很大。为此,本文提出了采用光顺–变形–映射–修正四个步骤来解决特征复制的方法,并进行了两点改进:1) 设计了一种多线外形的光顺算法,将多线外形的光顺分解成分层截面线的光顺,利用高斯光顺算法,通过建立同一阈值,快速实现多线外形的光顺;2) 提出了一种相似多线外形间的变形算法,将应用于细分曲面的收缩包围算法作用到多线外形个体的变形中,实现了多线外形的变形,通过映射得到新的特征曲线网,对于偏差最后设计了修正算法,采用曲线网构造相似的算法实现了曲线网的修正,得到理想的特征曲线网。
2. 截面线点云的高斯光顺
离散曲线是由像素坐标链而形成的代码序列,在滤掉噪声的同时保持曲线的基本形状特征是选择滤波器的关键。高斯滤波器是根据高斯函数的形状来选择权值的线性平滑滤波器,高斯平滑滤波器对去除服从正态分布的噪声有很好的效果。图像轮廓曲线S在数字化处理(对初始图像进行轮廓提
取和跟踪)后可被表述为平面上一列坐标为整数的有序点集合:
,对于一般的简单闭曲线(首位相连的曲线),其参数方程记作
,其中s为弧长参数,
。L为曲线的长度。则离散曲线用到的Gauss函数为:
,
其中
代表高斯分布的均方差。
曲线S经过Gauss核函数演化后为
,其中 ,
。经过Gauss光顺后
,
,
在本文中,我们仅把高斯光顺用到离散曲线,离散闭曲线须满足以下两个条件:① 如果两个点的序号相邻,那么这两个点在图像中的像素也是相邻的;② 两个邻域点之间的距离为1 mm (即使实际距离可能是
mm)。实际上,可能会有一些曲线不满足条件①,采用Gauss光滑算子对离散曲线进行光滑时,需要计算其离散形式。即在某一给定的尺度
下,计算
时
的值。对于离散曲线,我们采用如下方式计算
,
。经过Gauss光顺后
,
,
在本文中,我们仅把高斯光顺用到离散曲线,离散闭曲线须满足以下两个条件:① 如果两个点的序号相邻,那么这两个点在图像中的像素也是相邻的;② 两个邻域点之间的距离为1 mm (即使实际距离可能是
mm)。实际上,可能会有一些曲线不满足条件①,采用Gauss光滑算子对离散曲线进行光滑时,需要计算其离散形式。即在某一给定的尺度
下,计算
时
的值。对于离散曲线,我们采用如下方式计算 的离散值:
的离散值:
,
,
其中L的最大值可以取到曲线上点数目的一半,Z是整数。如果L足够大,那么
,高斯函数中的尺度因子
是决定光滑效果的重要因素。对曲线进行光滑时,光滑函数
采用的尺度不一样,得到的光顺效果就不一样。因此,可以设定一个阈值
,令
,对于不同的光顺要求给定不同的阈值。
3. 基于多线外形的特征曲线网变形
本文将变形分为初始变形和配准变形两部分:初始变形利用基于ICP算法的刚体变换和纵向缩放实现两个相似个体的初始对齐;配准变形通过收缩包围算法实现两个平面曲线的演化,从而完成多线外形的变形,并建立映射函数,最后把基于多线外形的特征曲线网通过映射函数投影,得到新个体上的特征曲线网。
3.1. 基于ICP方法的刚体变换实现初始变形
最近点迭代(ICP)算法 [7] 是应用最为普遍的数据配准算法,它主要通过迭代方式逐步逼近最佳结果,但是由于该算法的收敛速度较慢,并且不能确保能够收敛到全局最优点,因此当数据集的初始位置相差较大时,该算法可能会出现错误的配准结果,因此本文对最近点迭代(ICP)算法进行了改进,在使用该算法之前,对数据进行刚体变换,使数据集具有一个相对良好的初始位置。
首先引入了刚体变换,对于点集A中一个数据点
,写成齐次坐标的形式
,通过刚体变换矩阵H,可以变换成点集B中一点
,变化关系式为
,
其中H可以写成4*4的矩阵,
,R为旋转矩阵,T为平移向量。
对于数据集
,若数据集P经过变换矩阵H与数据集Q的误差表示为
,我们以
为目标函数,来求解非线性最优化问题
。根据误差度量选取点到点距离平方和作为目标函数:
那么,点云配准的目标误差函数可表示为:
(1)
运用四元数法求解刚体变换矩阵R,T。
然后,采用ICP算法进行点云配准,假设源点集和目标点集分别为S和G,令
,
,
,
。本文利用ICP的迭代算法分五步实现两个多线外形的对齐。Step 1:分别计算源点集和目标点集的质心
,
;Step 2:计算出最近点,对于
中的每个数据点,计算在目标点集G中的最近点
,此处选取距离最近点;Step 3:通过式(1)最小化目标函数,估计配准参数
,并计算误差
;Step 4:对源集更新,使用估计得到的变换矩阵
对源点集
进行更新,
;Step 5:重复迭代,直到两次计算的误差变化小于阈值,即
,停止迭代。
ICP算法能够保证得到的解局部最小,通过本节算法验证实例,得到了较好的初始配准结果,图4.6演示了通过ICP迭代进行初始变形的过程,其中图1(a)为三维变换后的两个多线外形,蓝色表示目标个体,红色表示经过ICP变形后的个体,图1(b)~(f)分别为迭代1,2,4,8,10次后的两个多线外形,可以看出,随着迭代次数的增大,两个多线外形越来越接近,表1给出了迭代过程中两个多线外形的平均误差。经过多次试验,本文将迭代终止条件设定为两个多线外形的平均距离小于5 mm,如表1所给个体需要迭代10次满足迭代终止条件。

Table 1. Mean error by ICP iterations
表1. ICP迭代过程中的平均误差
3.2. 收缩包围算法实现曲线演化
通过2.1节的初始变形后,建立两个截面线间的特征对应关系,对截面间距做平均化处理,通过插入和删除截面线,建立多线外形A和多线外形B间对应曲线的一一对应。本节通过收缩包围算法实现平面曲线的演化。收缩包围算法的主要思路就是每次细分后将吸引力和松弛力共同作用于网格顶点,其中吸引力将顶点拉向初始网格上的顶点最近点;松弛力保证顶点移动时局部变形能量最小,在平面曲线的演化过程中,利用此算法的思想,提出了基于曲线参数化的变形算法。
对于两条截面线,记做
和
,其中
为原曲线,
为目标曲线,为使原曲线变形成目标曲线,我们把
看做
,截面线
向
演化,演化的过程中不断产生过程曲线
(
,第r次演化),如果
存在断裂,也就是
上两个点的索引号是相邻的,这两个点在相关联的图像中像素不是相邻的,这个时候就需要使用线段离散化成像素点来修补轮廓线,修补后的轮廓线为
,
作为下一个演化的轮廓线接着向
演化,最终演化得到目标曲线。曲线演化的过程可分为五步进行:
Step 1:对于
上任一点
,首先在
上寻找最近点
,设定距离阈值
,通过判断
来决定Step 2还是Step 3,若满足
转Step 2,否则转Step 3;
Step 2:通过计算
在各自曲线上的法向
,
,若
,说明该点是有效点,将该点传给
;
Step 3:L是连接
上的所有点
构成的多边形,
也是连接曲线
上所有点构成的闭合的多边形。通过法向进行线段投影,将L上的点
投影到
,如果同时有好几个交点,选择到点
距离最短的交点,设交点在所在曲线上的法向为
,同时这个交点要满足
由于像素点都是整数点,求出的交点可能不是整数,要把交点整数化,这样就能获得了
上的点
。如果此点
满足Step 1中的条件,那么说明
是有效的,同时把这点传递到
,以便进行下一次的曲线投影;
Step 4:在演化过程中,检查 上的点,如果两个点
和
的索引号是相邻的,那么这两个点在相关联的图像中对应的像素不相邻的。就要使用线段离散化成像素,得到新的截面线
,作为下一轮轮廓演化的初始轮廓;
上的点,如果两个点
和
的索引号是相邻的,那么这两个点在相关联的图像中对应的像素不相邻的。就要使用线段离散化成像素,得到新的截面线
,作为下一轮轮廓演化的初始轮廓;
Step 5:计算两曲线距离
(演化后的曲线与目标曲线的距离,通过两条曲线上点的距离和计算)
如果
,停止迭代,否则
,转1。
上述算法的步骤Step1~Step3是曲线的变形部分,相当于收缩包围算法中的吸引力,Step4是曲线的离散部分,是用线段离散化成像素的方法来修补断裂的部分,相当于松弛力,在这两个力的作用下,使原曲线不断向目标曲线演化。
图2给出了本节曲线演化的示例,其中距离阈值 取2 mm,图中可见红色原曲线演化后的黑色星号曲线与蓝色目标曲线重合,经过曲线演化,可以完成两条曲线间的变形。红色表示原曲线,蓝色表示目标曲线,黑色星号表示红色曲线演化后的曲线。
取2 mm,图中可见红色原曲线演化后的黑色星号曲线与蓝色目标曲线重合,经过曲线演化,可以完成两条曲线间的变形。红色表示原曲线,蓝色表示目标曲线,黑色星号表示红色曲线演化后的曲线。
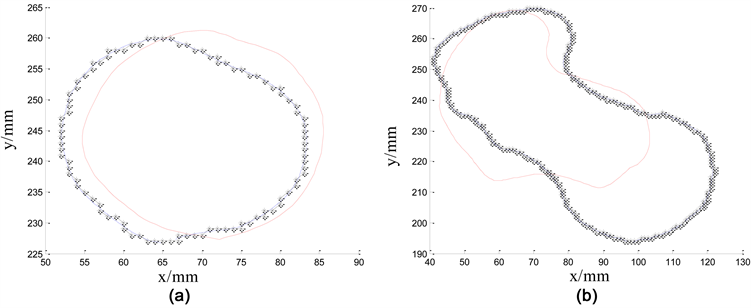
Figure 2. Evolution of plane curves. (a) Curve evolution of example 1; (b) Curve evolution of example 2
图2. 曲线演化。(a) 曲线演化示例1;(b) 曲线演化示例2
4. 特征曲线网的映射和修正
4.1. 特征曲线网的映射
为了实现多线外形的变形,由于多线外形是由截面线数据组成,而所有截面都在平行于xoy坐标面的平面上,经过初始对齐的两个个体,都是由一组平行于xoy坐标面的平面组成,因此,只需采用分层映射的思想,对两个个体的Z坐标建立映射,则可以建立两个截面间的映射,对这两条截面线进行曲线演化,就可以实现截面线的变形。
在对两个个体的Z坐标建立映射时,有两个需要注意的问题,1) 两个多线外形的截面线条数可能有多有少,2) 两个多线外形的截面间距可能不同。对于两个多线外形A,B,设它们的截面线条数分别为
,
,由于CT切片提取截面线时并不一定逐片提取,因此截面间距不一定是一个固定值,但是为了完成多线外形间的映射,我们需要把每个多线外形的截面间距固定,同时确保截面线条数相同是必要前提。解决上述两个问题主要分四步进行:
Step 1:对于两个多线外形,设截面线条数分别为
,
,若 ,转Step 2;若
转Step 3;
,转Step 2;若
转Step 3;
Step 2:将
精简到与
相同,从第一条到
条,隔行删除
条截面线,直到 .
.
Step 3:将
插值得到与
相同,从第一条到
条,隔行插入
条截面线,直到
。插值的方法采用
,其中
表示前一层截面线上的点集,
表示后一层截面线上的点集,
表示插值后得到的截面线上的点集.
Step 4:设两个多线外形统一截面线条数后共有
条,平均截面间隔为dis,设多线外形的高度(z轴方向长度)为
(
表示截面线上最大z坐标, 表示截面线上最小z坐标),则
,得到统一间隔dis后,分别对截面线调整z坐标,设第一层截面线的z坐标为
,则第i层截面线的新的z坐标为
经过上述两个步骤的调整,欲进行变形的多线外形A,B,具有相同的截面线条数和相同的截面间隔,于是可以建立一一映射关系。多线外形A的第i层截面线对应多线外形B的第i层截面线,因此我们可以利用曲线演化理论,将多线外形A的第i层截面线变形到多线外形B的第i层截面线。利用分层截面线变形来驱动整个多线外形变形其好处在于,截面线很好的保持了个体的形状,减少了曲面拟合产生的误差。
表示截面线上最小z坐标),则
,得到统一间隔dis后,分别对截面线调整z坐标,设第一层截面线的z坐标为
,则第i层截面线的新的z坐标为
经过上述两个步骤的调整,欲进行变形的多线外形A,B,具有相同的截面线条数和相同的截面间隔,于是可以建立一一映射关系。多线外形A的第i层截面线对应多线外形B的第i层截面线,因此我们可以利用曲线演化理论,将多线外形A的第i层截面线变形到多线外形B的第i层截面线。利用分层截面线变形来驱动整个多线外形变形其好处在于,截面线很好的保持了个体的形状,减少了曲面拟合产生的误差。
由于特征曲线网是由位于多线外形上的特征点组成,通过曲线演化后的前后两条曲线根据参数具有一一对应关系,因此通过多线外形的变形和特征曲线网的索引号我们得到了映射后的特征点集,同样具有特征点所在层号,特征点所在层的点序号,特征点所述的特征线号等几何信息。将映射后的特征点集按照特征线的顺序连接起来,得到如图3的映射后的特征曲线网,其中红线部分表示映射后特征线连接成的特征曲线网。
 (a)
(a)  (b)
(b)
Figure 3. Feature curve networks for hip femurs. (a) Feature curve network for hip femur 1; (b) Feature curve network for hip femur 2
图3. 股骨的特征曲线网。(a) 股骨个体1的特征曲线网;(b) 股骨个体2的特征曲线网
4.2. 映射后特征曲线网的修正
通过映射后得到的特征曲线网会出现三种不满足二维流形网规则的情况:1) 多余点2) 缺失点3) 不是特征点。多余点表现为误差明显偏大点或孤立点,这种点严重影响了曲线网的拓扑结构,因此需要把这种点从特征点集中剔除。缺失点表现为在特征线建立时,在曲率较大处缺乏描述弯曲的点,前两种点严重影响了曲线的光顺性,表现为坏点。不是特征点表现为即使特征线具有明显的光顺性,但是特征线上的点并没有在曲率极值处,该问题转化为如何把大曲率特征回归到原来位置。
图4描述了不满足二维流形规则的上述三种情况,在图4(a),类型1的点指多余点,这些多余点造成了曲线的错误连接,在图4(b)中,类型2指缺失点,可以看出该处两条曲线缺少结点连接,类型3指在股骨小转子处,虽然有条光顺的特征线,但是这条特征线没有较好的描述到小转子的特征。如图4所示。
针对映射后特征曲线网出现的上述三种情况,可以通过设计算法和交互式变换,完成特征曲线网的修正,使修正后的特征曲线网具有良好的拓扑结构和较好的光顺性。对于多余点和缺失点本文通过修改法和优化法 [8] [9] [10] 进行修正,对于类型3的特征点本文采用邻域内的曲率极值法来进行修正,下面给出股骨和髋骨修正后的特征曲线网,如图5所示。
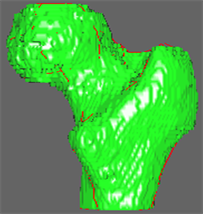
图5绘制了髋关节的多线外形及特征曲线网,在医学图形图像处理软件DateSet上对髋关节进行三维重建,图6给出了三维重建的髋关节股骨和髋骨及其上的特征曲线网。
5. 小结
本文以髋关节为应用对象,研究多线外形的特征曲线网复制方法。本文绕开复杂的特征曲线网

Figure 4. Feature curve networks after mapping for hip femurs. (a) Type 1: redundancy; (b) Type 2: the missing; Type 3: non-feature points
图4. 映射后需要修正的特征曲线网。(a) 类型1表示多余点;(b) 类型2表示缺失点;类型3表示不是特征点
 (a)
(a)  (b)
(b)  (c)
(c)  (d)
(d)
Figure 5. Modified feature curve networks. (a) Hip femur 1; (b) Hip femur 2; (c) Hipbone 1; (d) Hipbone 2
图5. 修正后的特征曲线网。(a) 股骨个体1的修正;(b) 股骨个体2的修正;(c) 髋骨个体1的修正;(d) 髋骨个体2的修正
 (a)
(a)  (b)
(b)
Figure 6. Three-dimensional reconstruction of hip joints. (a) For hip femur; (b) For hipbone
图6. 髋关节三维重建. (a) 股骨三维重建;(b) 髋骨三维重建
构造,而选用特征复制的方法,将已有的特征曲线网复制到具有相似外形的个体上,对多线外形进行高斯光顺,采用基于收缩包围算法的平面曲线演化,进行配准变形,实现了多线外形之间的映射,获得了映射后的特征曲线网,通过坏点修正和曲率点修正得到满足二维流形的二维曲线网。解决了医学图像领域的三维重建问题。
项目基金
国家自然科学基金(51175248/E050603);南京航空航天大学基本科研业务费资助(NZ2013201)。
NOTES
*通讯作者。