1. 引言
医院门诊大楼中的电梯调度方案的设计问题,针对以下的三个问题:电梯的使用、高峰时期的运载效率、复杂的电梯调度问题进行了分析。
第一问题,对于电梯的使用,考虑节约能源和尽力满足客户需求两个角度,确定了以用户平均等待时间,以及停靠次数作为电梯运行调度方案的两个主要指标,并据此建立模糊综合评价模型。其中,结合乘客心里特征以及电梯能耗特点,给出了平均等待时间与停靠次数对于不满意度的具体隶属函数,并考虑医院以效率优先的原则,确定了平均等待时间以及停靠次数两种不满意度的线性重要权重为0.8与0.2 [1]。
第二问题,电梯评价主要参考其高峰时期的运载效率。通过对医院高峰时期的人流分析,假设高分期分流服从
的正态分布,以及每个人去往医院的任意的楼层数服从1~29的离散均匀分布。进一步,设计了以计算机仿真进行统计计算每个候选方案平均等待时间和平均停靠次数的整理思路框架,对任意候选方案采取100轮次的高峰人流电梯调度仿真。对具体每一轮高峰人流电梯调度仿真,进一步建立了电梯运行流程模型。最终,使用MATLAB实现了单次高峰人流调度计算以及整体仿真估计流程,并针对电梯停靠的常用的单双层和高低层一共7种方案,进行了100次的仿真计算并获得了每个候选方案的平均等待时间和停靠次数,具体结果详见下文6.3.3。将所得结果代入问题一的模糊综合评价模型中,最终获得不满意度最小的最优调度方案为高低层电梯分配调度方案,其中A、C电梯停靠范围4~17与B、D电梯停靠范围18~29,其不满意度值最小位为0.1503。
第三问题,要求结合实际情况,进一步对我们对问题二中的方案作出调整,用于解决更为复杂的电梯调度问题。故考虑在第二问的基础上,进一步考虑来自地下车库的乘客需求,将第二题的候选拿方案包含兼顾对于地下停靠点的选择。沿用第二问在整体计算流程思路上,但是具体每轮的高峰人流由地下车库的需求以随机0.08概率产生,并计算考虑每轮电梯作业新增的对运行时间以及每位乘客等待时间的延迟。最后,针对电梯停靠高低层一共7种方案,进行了100次的仿真计算并获得了每个候选方案的平均等待时间和停靠次数,具体结果详见下文6.4.2。将所得结果代入问题一的模糊综合评价模型中,最终获得不满意度最小的最优调度方案为高低层电梯分配调度方案,其A、C电梯停靠范围−1,−2,4~16与B、D电梯停靠范围−1,−2,17~29,其不满意度值最小为0.1506。
2. 电梯调度问题提出
作为医院的垂直交通工具,人们对电梯的需求变得越来越复杂。在每天就医人数高峰期,医院电梯是非常拥挤的,医院在要求减少电梯设备占用建筑物的核心空间的同时,希望电梯交通系统的服务数量和质量有大幅度提高。因此,如何对现有资源合理利用,缓解电梯的运输压力,缩短病人和医生的等待时间,是医院所必须解决的问题,也是电梯垂直交通系统面临的新的挑战。
徐州市中心医院拟在铜山区新建一个31层的门诊大楼,其中含有地下二层(地下二层为停车场,地下一层为药品及医疗器械运送场所)。门诊大楼内部设有四部电梯,编号分别为A梯、B梯、C梯、D梯,其中A梯、B梯为无担架病人及家属专用电梯,每个电梯最多载重1350千克;C梯、D梯为有担架病人及医生专用电梯,每个载重1000千克。每个电梯内部有33个按钮,其中包括开门按钮、关门按钮和楼层按钮,编号为−2,−1,1,2,3,4…,29。电梯外部含有两个按钮,即向上运行按钮和向下运行按钮。建筑顶层与地下二层例外,建筑顶层只设置有向下运行按钮,地下二层只设置有向上运行按钮。电梯开关门完成时间设定为1秒。电梯到达每层后上下人的时间设定为8秒。电梯从静止开始运行到下一层的时间设置为2秒,而运行中通过一层的时间为1秒。在凌晨2:00~4:30之间,如若没有请求信号,A梯、B梯自动停在16层,C梯、D梯自动停在6层。当电梯下到−2,−1层后,如果没有请求信号,电梯自动回到1层。徐州市中心医院的门诊大楼一楼平面图见下见图1:

Figure 1. Floor plan of the outpatient building of Xuzhou Central Hospital
图1. 徐州市中心医院的门诊大楼一楼平面图
请针对徐州市中心医院就医人数高峰期的情况(高峰期需要使用电梯500~1000人次),对电梯调度问题建立数学模型,以期获得合理的优化方案。
问题1:给出若干合理的模型评价指标;
问题2:针对徐州市中心医院门诊大楼情况给出一个合理的调度方案;
问题3:在第二问的基础上,将数学模型进一步实际化,提出合理化的建议和措施,用于解决更为复杂的电梯调度问题。
3. 模型假设
假设1:所有乘客乘坐电梯时均遵循先到先乘坐的规则;
假设2:普通病人与医生也乘坐C梯、D梯,只是出现有担架病人及医生时,优先让有担架病人及医生乘坐,为简化问题,通常认为有担架病人及医生占总体比重较小,所以由这部分产生的等待时间不计;
假设3:假设人均体重为65 kg,即A梯、B梯最大承载20人,C梯、D梯最大承载15人;
假设4:在高峰期,医护员工上班,以及病人就医来到医院的时间整体服从正态分布
;
假设5:三层及以下楼层的员工上下楼忙时走楼梯,闲时乘电梯;四层及以上楼层的员工上下楼均乘电梯,不走电梯;
假设6:客运电梯在7~9时上班高峰时上行运行停靠,下行时不在途中停靠;
假设7:电梯使用者到达电梯时,通常不会等待未到达达的其他乘客过长时间,所以设电梯的整体满载率为50%;
假设8:问题2中不考虑地下车库。
4. 符号说明
:人均等电梯时间;
:大规模仿真的平均人均等电梯时间;
:停靠次数;
:大规模仿真的平均停靠次数;
:人均等待电梯时间不满意度隶属值;
:平均停靠次数不满意度隶属值;
:电梯承载率;
:该电梯当前批次的最终出发时间,也就是当前批次最后一个人的到达时间;
:该电梯当前批次的最大出发楼层,也就是电梯需要运行的最高位置,到达后即返回。
5. 概念引入及问题分析
5.1. 概念的引入
分层次运行方式:每部电梯负责一定的楼层,只在其负责的楼层和底层停靠,例如规定电梯负责的楼层是11~15层,则该电梯只能停留于11~15层。单双层运行方式:电梯只在单层或双层停靠,例如电梯为单层运行,则该电梯只能在单层(1、3、5…层)停靠。电梯直达某高层以上运行方式:电梯只能在规定的楼层及其以上的任意楼层停靠,而不能在规定以下的楼层停靠,是分层次运行的一种方式。
5.2. 问题分析
对于问题1,要求我们给出若干合理的模型评价指标,对于电梯的使用,可以考虑节约能源和尽力满足客户需求两个角度来具给出电梯运行方案的评价指标。问题2要求针对徐州市中心医院门诊大楼情况给出一个合理的调度方案,可以考虑我们在常用的电梯运行方案中例如单双层停靠与高地层停靠等方式中选择合适的方式,根据问题的评价指标对其进行评价选择。问题3要求在第2问的基础上,将数学模型进一步实际化,可以进一步考虑电梯运行细节,楼层使用,在更为复杂的电梯调度过程中问题,根据问题一的指标对相应的方案进行选择。
6. 模型的建立与求解
6.1. 模型准备与分析
6.1.1. 电梯停靠方案
高楼建筑常用的电梯停靠方式主要有两种,分别为单双层与高低层停靠方式,在本文的医院高楼设定中,ABCD四部电梯,可以采用如下表1所示的电梯停靠方式。

Table 1. Each elevator parking mode
表1. 每台电梯停靠方式
由于在医院中,C梯、D梯为有担架病人及医生专用电梯,所以必须满足这两梯覆盖所有楼层的停靠点。同时,剩余电梯为了满足其他乘客的电梯使用也应满足覆盖所有楼层的停靠点。进一步,根据各类电梯的数量,表1展示了最为合理的单双层和高低层电梯调度分配方式。
6.1.2. 高峰时刻
对电梯调度方案的优劣,主要在于其高峰时刻调度性能的优劣,为此我们对医院高峰时期人员乘坐电梯的过程进行模拟。我们设定人员到达的时间分布为正态分布
,员工到达后,三层及以下楼层的员工走楼梯,四层及以上楼层的员工乘电梯,所有人乘坐电梯时均遵循先到先乘坐的规则。我们结合员实际电梯使用高峰时间分布情况经过试模拟后认为二者的较优取值为:
,
。
由员电梯使用高峰时段人员到达的时间分布(见图2(a),其中横轴为时间(单位:秒),纵轴为人数)可知,该高峰时间为持续两个小时,该过程发生在7点至9点之间,此时段内医护人员上班以及早晨就医人员大量进入,造成该时段内的电梯使用的高峰。
 (a)
(a)  (b)
(b)
Figure 2. Data distribution: (a) Arrival time distribution map; (b) Map of arrival levels
图2. 到达数据分布:(a) 到达时刻分布图;(b) 到达层数分布图
对于到达人数,根据题意,高峰期需要使用电梯500~1000在本问题中,我们设置高峰使用人数为该区段的中点750人,并且所有人员从1层前往1~29层的数量程均匀分布,上图2(b)给出了所有750人在某次高峰时段达到不同医院楼层的人数分布。从上图可以看出,各层停靠需求相对均匀,而实际中若有相关停靠位置分布数据可依据实际分布模拟,此处由于缺少数据,就用均分分布代替。
6.1.3. 电梯运行过程
由于关于电梯的问题类似,所以为了找到比较通用的解决办法,我们决定设计算法以便于对人乘坐电梯的过程进行模拟,得出必要的数据,最后对电梯的运行方式进行评价。高峰期间内,人员的到来服从对时间的正态分布,人工到来之后在停靠自己所在楼层的电梯前排队,其中不包括1、2、3层的员工。在电梯运行一周的过程中,不断的向需要停放人员的楼层停靠直到最高层,电梯运行一周的步骤过程如下:
Step 1:电梯开门,排在前面的一定数量人依次进入电梯,电梯门关闭,向上行驶;
Step 2:判断第i层是否有人下。若无,则不在第i层停靠,电梯驶向第i + 1层。若有,则电梯在第i层停靠,开门,要出人员依次走出电梯,关门。令i = i + 1,判断电梯是否达到最高期望楼层,若否向Step 2开头,若是则转向Step 3;
Step 3:电梯停靠在最高期望楼层,电梯中人员已全部下完,驶向靠在一层。
6.1.4. 方案设计思路
在电梯的调度方案设计中,我们需要在第一问中确定,电梯调度方案的评价指标,并依据评价指标建立起电梯方案的模糊评价模型。在第二和第三问中,我们采用编程实现各种备选方案的调度算法,结合医院电梯和高峰人流实际数据,对每种备选方案仿真100次,获得人均等待时间
和停靠次数的平均值
,并代入第一问中确立的模糊评价模型对每个候选方案进行评价,评价结果最优的方案即为我们所选择的医院电梯调度方案。具体的思路流程可以归纳为如下图3的思路流程图。

Figure 3. Design flow chart of elevator dispatching plan
图3. 电梯的调度方案设计思路流程图
6.2. 问题1——电梯调度方案评价指标
6.2.1. 评价指标
关于电梯评价的两个方面,我们节约能源和尽力满足客户需求两方面出发去寻找。在尽力满足用户需求方面,尤其是在医院这种服务机构内,可以认为是首要需满足的重要指标。对于每个电梯用户而言,尽可能少的等待时间可以被作为最主要的考查标准 [2]。
另一方面,在尽可能缩短用户等待方案时间的调度方案下,应该尽可能减少电梯的能耗,在电梯的使用中,如果越是集中目标楼区的人群在一次承运作业中,减少频繁多点的停靠,能够有效的起到节约能源的作用。
综合上述分析,本文选取如下两个指标作为电梯调度方案的评价指标。
6.2.2. 电梯调度方案模糊综合评价方法
1) 平均等待指标的隶属化
我们首先处理等待时间。我们定义等待时间取下列值时,不满意度也如下表2变化:

Table 2. Dissatisfaction with waiting time
表2. 关于等待时间的不满意度刻画
注:当等待时间大于1000 s时,可认为员工已经“麻木”,因此态度也是很不满意。
由于人等待的心理时间与现实时间成二次函数,所以为了连续量化指标,我们采取二次函数和对数函数最为隶属函数:
其中 a,b,c,d 为待定常数,且有:
a) 当很满意时,隶属度为0,即
;
b) 当较满意时,隶属度为0.8,即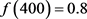 ;
;
c) 当很不满意时,隶属度为1,即
。
由于在上述定义中,自变量与因变量的数量级之比有1000倍之多,拟合出来的参数数量级一定很小,这往往会造成最终拟合出来的参数会不精确。为了使各类待定常数更加精确,我们让等待时间的数值缩
小200倍,这样减小了它们之间的数量级差距。即
。因此,上述隶属函数的定义可以更改为:
,
,
。
最终求得
。则