1. 引言
自从1963年,White [1] 和Akaryan [2] 等在首次试验上探测到脉冲激光激发超声波以来,激光超声技术由于其非接触、可远距离操作、可以在高温高压等不良环境条件下实现缺陷检测等优点而蓬勃发展起来 [3] 。而且激光脉冲无需耦合剂,激发出来的超声波信号具有宽频带和多模式的特点,这使激光超声具有许多传统超声技术无可比拟的优点 [4],然而这项技术多应用于金属等各向同性材料的缺陷检测。对于在木材和木质材料这种特殊的有机材料中激发超声波的理论和实验研究鲜有报道。同时虽然声超声技术在木材无损检测技术中是一项成熟的技术 [5] [6],但超声信号在木材中如何传播,缺陷对超声信号如何影响还只能通过透射和反射信号的接受获得综合的评估,对其在内部的传播机制还缺乏直观的了解。本文通过虚拟仿真激光超声在木材中的激发和传播过程,以及缺陷对超声的影响,直观还原超声信号在木材中的传播特性,为激光超声技术在木材中应用提供数值和理论指导。
激光激发超声波原理主要是热弹机制 [7] [8] 和烧蚀机制 [9] 。热弹机制是固体中激光产生超声的主导机制。当脉冲激光束撞击在材料上,部分被它吸收。被材料吸收的光功率转化为热,导致局部温度的快速增加。这导致了局部区域的快速热膨胀,导致表面和内部微小形变,产生超声波进入介质。
在平面应变理论中,忽略激光的温度效应,采用激光等效力源为激发源,激光等效力源的时域函数表示为:
(1)
式中
为脉冲宽度控制函数,t0为脉冲延迟时间;
为脉冲中心角频率。(1)式经过快速傅里叶变换即可得到激光等效力源的频域函数。
(2)
在进行超声的激发和检测时,相比于温度和应力的变化,我们更关心声波的传播的探测,由姆霍兹方程,可以得到声波的传输方程:
(3)
为声压随着时间的变化项,
为声传导引起的变化,
为声源项,
为
总的声压。
,
为激光产生的超声场的声压,
为初始的声压,主要是外界大气压引起的声压。通过计算每个格点的声压,我们可以得到每个格点处的超声波随时间的分布情况,为我们进行激光激发超声波的探测和传播提供依据。
本文中应用了有限元软件,应用平面应变理论研究超声波在木材激发机制,分析超声波在木材内部的传播机制,最后研究激光超声技术在木材无损缺陷检测方面的应用。
2. 模型的建立
2.1. 激光在木材中的超声激发机制
根据公式(1),激发参数分别为中心频率
,
,
,图1(a)激光等效力源时域波形,为尖脉冲信号。有限元频域模型激发源进行傅里叶变换得到激光等效力源的频域,如图1(b)所示,可以看到激光等效力源是宽频带激发源,频率与脉冲激光源的宽带特性吻合很好 [10] 。由图可看出脉冲信号激发的频率范围达到107 Hz,满足超声检测的频率要求。

Figure 1. (a) The time domain wave distribution of an equivalent force source of laser; (b) Spectrum diagram of an equivalent force source of laser; (c) Solid wood panel model
图1. (a) 激光等效力源时域波形;(b) 激光等效力源频谱图;(c) 实木板材模型图
2.2. 木材模型建立
为简单起见,我们如图1(c)所示的长方形木块模型,其中长10 cm,宽4 cm和高2 cm。虽然木材的种类不同,木材的密度不同,而且同一木材,在不同的位置密度也有区别,但是同一木材取在体积较小范围内,木材声速密度等相差不大,因此在文中的仿真中忽略了木材密度的变异性,做了各向同性的近似。在此因此虽然图中画出了年轮,我们假设此木块认为各向同性的材料,取木材的密度为530 kg/m3,杨氏模量为0.8 × 109 N/m2,声速为1950 m/s。
当我们采用此脉冲激光作用于木块模型表面中心时,图2表示激光激发到表面时两个不同时间
和
时的表面的位移和应力的分布。由数值模拟可看出,激光脉冲可有效在模型中激发较强的位移和应力,且随着时间的变化,由于脉冲力的作用产生了内部和表面的应力和位移大小和相位随之变化,形成明显的应变和位移以波的形式向外扩散和传播。仿真结果表明木材在激光等效脉冲力作用下,会出现热弹机制下的超声激发。
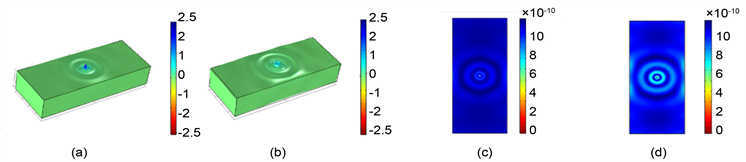
Figure 2. (a) The stress distribution at
; (b) The stress distribution at
; (c) The displacement distribution at
; (d) The displacement distribution at
图2. (a)
应力分布;(b)
时应力分布;(c)
位移分布;(d)
时位移分布
2.3. 多孔性对超声信号的影响
由于木材是一种多孔的复杂高分子材料,多孔主要体现在管孔和纹孔。其中管孔是中空状轴向输导组织,纹孔是相邻细胞间的水分和养分的通道。虽然超声波长相对于应力波较短,更易能检测到木材中微小的缺陷,然而木材遍布的纹孔其尺寸与超声的波长接近,对超声的传播产生很大影响,因此在仿真中纹孔和管孔必须作为一个重要的因数必须考虑。在仿真中,我们假设木块中纹孔和管孔均匀分布,孔隙率为0.35 [11] 。
图3是木块模型在不考虑纹孔管孔和有纹孔管孔时截面超声传播t = 8 us时域场图和傅里叶变换的频谱图。由于模型中设定为各向同性,在表面激发的超声信号在横截面上可看出以球面波的形式先前传播(图3(a)和图3(b)),但由于孔隙存在(图3(b)),超声波在界面的分布还是发生变化,在存在纹孔的截面中,出现更多的强弱部分不同的超声波,这是纹孔对传播超声波的反射导致入射和反射信号叠加形成的。在发射信号的对面加一接受传感器,同时将接受信号进行快速傅里叶变换,图3(c)和图3(d)是有无纹孔管孔和有纹孔管孔时的接收信号的频谱图。在超声信号低于0.5 MHz时,多孔和无纹孔管孔的频谱信号几乎一致,但超过0.5 MHz~1 MHz时,多孔时高频信号明显减少,说明纹孔管孔对该频率的信号出现较大的共振吸收,与图3(b)出现信号强弱分布一致。说明在有纹孔管孔时,当信号的频率较高,波长较短,和孔的尺寸相差不大时,超声信号被纹孔管孔共振吸收。
在实际木材中,除了纹孔管孔以外,由于木材是一种复杂的高分子材料,其主要成分纤维素、木素和半纤维素存在多样的主链和侧链结构,在超声信号作用,同样会出现共振吸收和阻尼现象,对反射和透射的超声信号产生影响,在仿真实验中没有考虑,将在后期的研究中用类似纹孔的形式设定多链结构对超声的影响。
3. 缺陷的数值仿真与分析
3.1. 木块缺陷模型
采用激光激发超声波进行缺陷检测,激发超声波种类丰富应用面广。主要通过激发横波、纵波、lamb波和rayleigh波。其中Lamb波是固体平板中传播的一种弹性波,这使得激光激发lamb波在板状结构的缺陷检测方面发挥重要作用 [12] [13],因此在检测木质板材和多层胶黏层积材缺陷时有重要的应用。以图1(c)木块模型为例分析激光超声在木材存在缺陷时的传播规律。首先脉冲激光点源作用到木材上表面的中心,设置两种缺陷,一种是内部空洞,宽度1 cm,长度1.5 cm,厚度5 mm。第二种是近表面缺陷,长
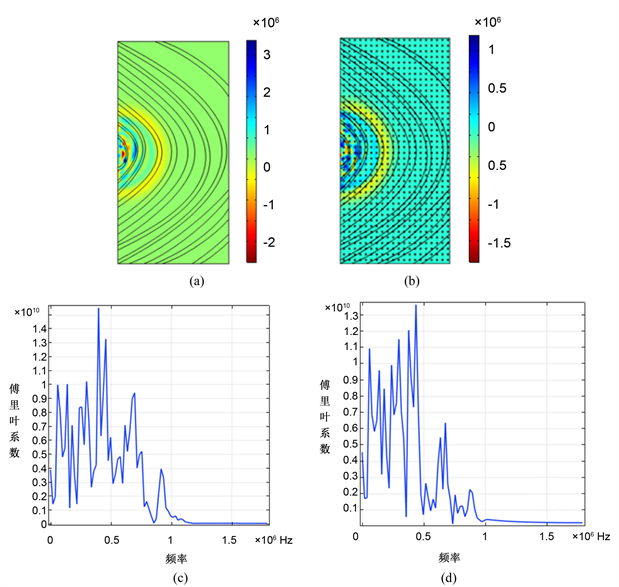
Figure 3. Effect of porous wood panel on ultrasonic propagation. (a) The ultrasonic propagation of no porouswood panel at t = 8 us; (b) The ultrasonic propagation of no porouswood panel at t = 8 us; (c) The spectrum diagram of no porouswood panel at opposite receiving points; (d)The spectrum diagram of porouswood panel at opposite receiving points
图3. 木材多孔特性对激光激发超声传播的影响(a) t = 8 us时假设无孔条件的超声波的传播图;(b) t = 8 us时考虑纹孔管孔时超声波的传播图;(c) 无孔条件对侧接收点频谱图;(d) 考虑纹孔管孔时条件对测接收点频谱图
1.5 cm,宽1.5 mm,深度1.5 mm。
3.2. 激光激发超声波测内部缺陷
用1 MHz中心频率的激光脉冲作用在在木块表面中央,图4超声信号在纵截面在三个不同时间的声压图,其中图4(a)为t = 7.4 us,图4(b)为t = 9.2 us,图4(c)为t = 13.4 us。随着时间的增大可以看到超声信号的传播特点。由于缺陷的存在,当超声信号遇到内部缺陷时,首先在表面存在较强与入射方向相反的反射波,时间越长,反射信号作用越明显,同时在缺陷的边缘由于衍射的缘故仍然有传播波传播。但在缺陷的方向,传播的超声波明显减弱。因此在激发源附近的接收传感器可以接收到有缺陷反射回的超声信号,当然也可通过在源的对侧,接受减弱的透射信号。为了进一步了解缺陷对传播信号的影响,将源对侧的超声接收器信号进行FFT变换得到图5频域图。图5(a)和图5(b)分别是无缺陷和有缺陷时接受的信号的频谱图。由纵截面的频谱图可看出有缺陷时,不仅高频成分的强度明显减弱,而且部分频率在频谱图上消失,也就是除了缺陷反射了部分高频成分,导致强度降低外,缺陷作为空腔,当尺寸与部分频率

Figure 4. Propagation of ultrasonic in the longitudinal section (a) t = 7.4 us; (b) t = 9.2 us; (c) t = 13.4 us
图4. 纵截面超声波传播图(a) t = 7.4 us;(b) t = 9.2 us; (c) t = 13.4 us
超声信号的波长一致或成整数倍时,形成超声谐振,吸收了部分超声信号。
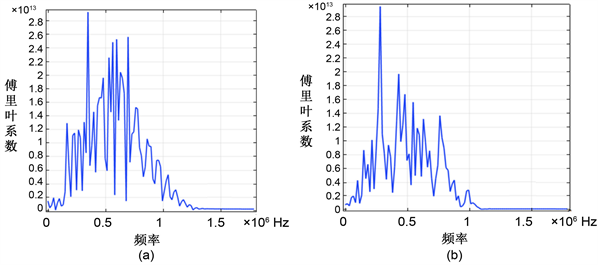
Figure 5. Propagation of ultrasonic in the longitudinal section (a) t = 7.4 us; (b) t = 9.2 us; (c) t = 13.4 us
图5. 纵截面超声波传播图(a) t = 7.4 us;(b),t = 9.2 us; (c) t = 13.4 us
3.3. 激光激发超声波测木材表面缺陷
激光超声信号另一个特征信号是沿表面的超声波,也称Rayleigh波。Rayleigh波是由结构形变产生的内部应力与应力形成,由于结构表面的应力自由,固体结构表面的rayleigh波沿结构的表面传播,而在结构的深度方向,瑞利波的振幅迅速衰减 [14] [15],因此可以非常灵敏的检测近材料表面及亚表面结构缺陷。
图6同样用1 MHz中心频率的激光脉冲作用在在木块表面中央,在表面长1.5 cm,宽1.5 mm,深度1.5 mm的表面缺陷时,Rayleigh波随时间变化规律。图6(a)~(c)分别是t1 = 3.4 us,t2 = 5.9 us和t3 = 6.75 us的表面波传播图。由图可看出,相对于沿径向的超声波,产生的表面波强度更大,看出随着时间的变化,rayleigh波遇到表面缺陷时,部分超声波会绕过孔隙的边缘呈现路径弯曲,在缺陷的背后展衍,但同时产生较大的反射波。如果在源与表面缺陷之间放置表面波传感器,接收到的声波频谱图可以看出当存在表面缺陷时(图7(a)),由于较强的声波反射,造成频谱图中高频超声明显增多,信号的明显差异可以灵敏的判断表面缺陷的有无。同时可以看出表面缺陷与木材内部缺陷不同,在引起表面波反射的同时,在表面缺陷中激发更多的高频信号(图5)。
随着扫描激光源技术的发展,线源激光可以实现沿着样品材料表面进行一维或者二维扫查 [16] [17] [18] 。扫描式移动光源以激光线源的形式进行大幅面扫描。在实际中采用线源进行扫查式激光超声检测不仅可以节省时间,而且可以实现大规模的工业化要求 [19] 。我们在此研究扫查式激光超声技术在木材无损检测中的应用。尝试反射法、透射法对样品材料进行激光超声扫描成像检测,以检测缺陷的存在。同样
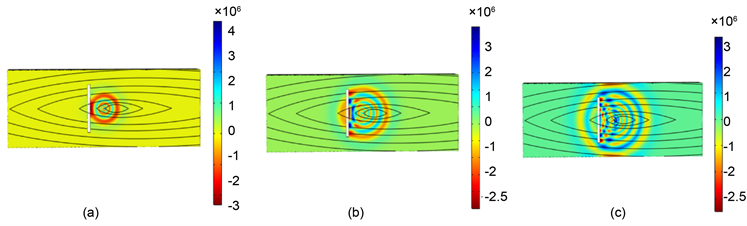
Figure 6. Propagation of acoustic in the board surface (a) t = 3.4 us; (b) t = 5.9 us; (c) t= 6.75 us
图6.板材表面声波图(a) t = 3.4 us;(b) t = 5.9 us;(c) t = 6.75 us
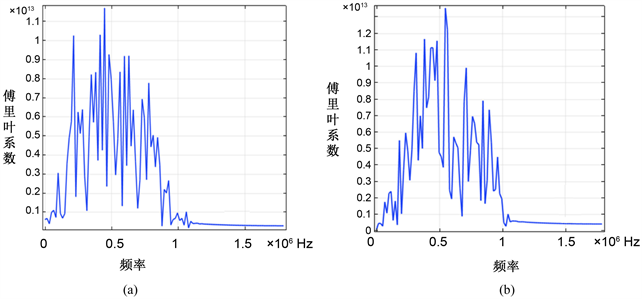
Figure 7. Acoustic Spectrum diagram of the receptor (a) Surface defects located between the laser source and the receptor; (b) No surface defects
图7. 接收器接受的声波频谱图(a) 存在表面缺陷;(b) 无表面缺陷
加载中心频率1 MHz线源在实木板材中来进行数值模拟得到三维板材的声场图。图8从三维立体角度展示了加载激光线源以后横波纵波和表面被的激发。图9和图10分别采用截面的形式展示了激光激发超声波在实木板材内部和表面的传播。可以很清晰的看到当超声波遇到空洞时,都会发生明显的声波反射透射。可以在图9和图10(c)中清晰的看到反射波和透射波的存在。同时可以发现采用扫查式激光超声检测可以激发更大幅面的表面波和内部横纵波,实现大范围快速检测。

Figure 8. Distribution of sound pressure in three-dimensional solid wood (a) = 3 us; (b) = 9 us
图8. 三维实木板材声压图t (a) = 3 us;t (b) = 9 us

Figure 9. Propagation ultrasonic in longitudinal section of solid wood (a) 9 us; (b) 15 us; (c) 18 us
图9.实木板材纵截面超声波传播图(a) 9 us;(b) 15 us;(c) 18 us

Figure 10. Propagation of ultrasonic in surface of the solid wood (a) 3 us; (b) 6 us; (c) 12 us
图10.实木板材表面超声波传播图(a) 3 us;(b) 6 us;(c) 12 us
4. 结论
本文采用平面应变理论探究了激光在木材中的超声波激发机制,利用数值仿真探究了木材的多孔性对于激光激发超声波传播的影响。并在此基础上数值分析了激光超声在木材内部存在缺陷时的传播特性,以及木材表面存在缺陷时Rayleigh波传播特性。在木材中利用激光超声研究其传播规律,不仅有助于丰富激光超声理论,更重要的激光超声技术在木材和木质材料无损检测中的应用,将为木材和木质材料的无损检测提供新的途径。
NOTES
*通讯作者。