全直流供电建筑储能最优运行策略研究

Research on Optimal Operation Strategy of All-DC Power Supply for the Building Energy Storage

摘要: 与传统交流供电建筑相比，全直流供电建筑在安全、经济和电能质量优化等方面具有较大的优势。研究全直流建筑储能最优运行策略，主要目的在于通过建筑全直流配电/用电，协同调用建筑内部储能合理充放电，对城市电力负荷日用电波动带来的峰谷差问题进行充分调整和优化。基于以上概念，对某接入多种新能源设备的新型全直流供电建筑的逐时发电、逐时能耗等进行模拟仿真，获取多种设备的发电、储能与用电曲线，建立供电数学模型。对恒功率电网取电、最优电价取电以及需求侧响应取电等方式进行相应运行策略优化，并得到运行策略方案。

Abstract: Compared with traditional AC power supply buildings, the All-DC power supply buildings have great advantages in terms of safety, economy and power quality optimization. Studying the optimal operation strategy of the All-DC building’s energy storage, the main purpose is to coordinate the charging and discharging of the internal energy storage of the building through the construction of the All-DC power distribution/electricity, and the peak-to-valley difference caused by the fluctuation of urban power load daily electricity consumption could be fully adjusted and optimized. Based on the above concepts, a new type of the All-DC power supply building with a variety of new energy equipment, time-of-day power generation, time-consuming energy consumption, etc., simulation, acquisition of power generation, energy storage and power consumption curves of a variety of equipment, establish power supply mathematics model. The operation strategy is optimized for the power supply of the constant power grid, the optimal power price and the demand side power take-off, and the operation strategy is obtained.

1. 引言

预计2019年中在深圳低碳城核心区域建成的中美中心零碳科研办公大厦，全楼共12层，其中科研、办公场地为5000平方米。大厦全部电器设备，含空调、照明、电动汽车充电、科研与办公电器、设备，楼宇智能监控等均采用集中式交直流转换DC±375V和DC48V全直流供电，是国内最大的采用全直流供电的科研、办公建筑 [1] - [7] 。利用低压直流配电，可充分减少变电设备个数、提升配用电系统整体效率，提高用电设备安全性，通过集中式交直流电能变换电能质量动态补偿，有效降低输入电网的谐波、无功及不平衡电流，同时在离网状态下通过直流建筑内部储能，保持建筑的不间断供电，具有安全性、经济性和高电能质量等优势。

储能最优运行策略 [8] - [16] 是研究全直流供电建筑的关键内容之一。区别于传统交流建筑负荷峰谷值大、用电负荷不可调节的既有缺陷，全直流建筑通过引入蓄电池储能作为能量缓冲器，实现电网取电由实时取电向延时取电的有效调节。另外传统交流供电建筑普遍使用低于90%输电效率的整流/逆变器件将储能电池与配电交流母线并联，全直流供电建筑采用最高效率98%以上的双向柔性直流变换器件与建筑直流母线并联，又由于直流建筑采用集中式交直流电能变换，变电效率亦高达98%以上，因此可实现电能的高效存储与释放。调节方式为：1) 电网缺电、停电或电力成本较高状态下，通过建筑内部储能放电补足建筑内用电设备需求部分；2) 电网富电或电力成本较低等状态下，通过建筑内部储能从电网取电充电，将电能储存到需要放电时使用；3) 建筑储能以一定周期进行循环充放电，使得建筑负载在电网侧表现出可调节特性，部分或全部满足电网对建筑的负荷特性需求。然而包含储能电池造价、建筑占地以及高密度储能安全维护成本等在内的建筑储能建设成本高昂，配置容量往往不能充分满足电网对于建筑储能完全调节建筑负荷功率的要求，只能在建筑成本经济性和建筑储能的调节效果之间做适当的平衡。由此引出建筑储能不充分状态下，灵活调配充放电能源走向，制定建筑储能最优运行策略的问题。

储能设备常见的储能运行策略有：1) 基于电网恒功率或准恒功率输出的储能动态调节策略，通过控制电池按照“电网以恒功率或准恒功率取电”的目标进行动态充放电。恒功率取电的优势在于从电网侧看来本栋建筑为恒功率负载，因此可以有效减少电网侧预装式变电站的安装容量，同时有效降低电网调峰储备容量，从而有效降低电网建设成本。由于储能电池在长期工况下收纳能量与释放能量平衡，因此恒功率取电策略的控制目标通常以24小时内恒功率为控制目标；2) 基于实时电价的储能动态调节策略，市政电网根据用电负荷状态，制定分时电价。建筑直流供电系统可根据市政电网的价格信号，对电池充放电功率进行动态管理，调整从电网取电的功率，达到建筑供电系统运行的经济性最优化；3) 基于需求侧响应的储能动态调节策略，为了提高电力系统运行效率、安全性和能源资源利用水平，通过各种激励手段促使电力用户改变用电行为，实现负荷的调节和转移。基于需求响应的策略是指根据电网的需求响应规定，确定不同的分时取电功率进行储能充放电调节。

以上3种运行策略采取的控制手段与实施方案在实现方式上基本一致，因此本文以策略1) 电网恒功率取电运行策略为研究对象进行优化设计。本文通过建立结合储能的直流建筑供电模型，对研究对象在储能不充足情况下的最优充放电策略进行深入研究，提出2项准恒功率电网取电状态下的达成情况评判值。通过该2项评判值研究不同储能调节策略对电网准恒功率输出的优化情况。基于既有建筑设计方案，采用建筑能耗模拟软件得到冬、夏不同工况下的建筑24小时负载能耗模拟值，并验证比较了多种优化方法对电网输出功率峰谷波动的调节作用的调节效果。

2. 全直流建筑供电模型

Figure 1. Zero-carbon research office building full DC power supply system topology

图1. 零碳科研办公大厦全直流供电方案系统拓扑

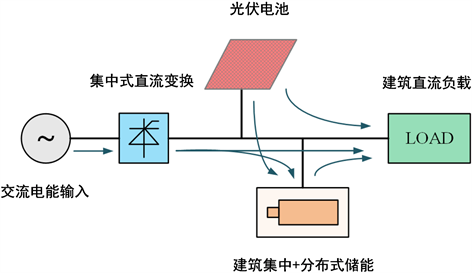
Figure 2. Zero-carbon research office building power supply model

图2. 零碳科研办公大厦供电模型

如图1、图2所示分别为中美中心零碳科研办公大厦全直流供电方案系统拓扑和供电模型。采用电网取交流电，经集中式电压源换流器转为直流 ± 375 V与光伏发电并联供电，供大功率直流设备使用。直流 ± 375 V经直流建筑配网逐个接入楼层配电箱，转为直流48 V超低压电源供小功率科研、办公电器使用。同时通过调节蓄电池充放电功率，既满足建筑的用电负荷，又同时达到改变电网取电曲线的目的。其中：

电力来源：

1) 电网取电：可取功率为DC2 × 200 kW；

2) 光伏发电：最大取电功率约100 kWp；

电能存储：

1) 集中式储能，布置于集中储能柜内，约100 kWh；

2) 分布式储能：分别布置于空调、房间等空间内，有效储能量约30 kWh；

电能消耗：

空调、照明、充电桩、数据中心、办公电器、应急系统等，日常用电峰值150 kW，年平均用电约40 kW。

3. 优化目标与优化方式

建筑储能作为用户侧能量缓冲设备，能量来源为电网和光伏发电系统，能量去向为建筑直流负荷。通过调节储能电池的充放电功率，既满足建筑的用电负荷，又同时达到改变电网取电能量曲线的目的。

优化目标为通过优化储能动态充放电量，优化直流建筑24小时内的每小时电网取电量曲线。

设：

$W=\left[w_1,w_2,\cdots ,w_{24}\right]$ (1)

$V=\left[v_1,v_2,\cdots ,v_{24}\right]$ (2)

$B=\left[b_1,b_2,\cdots ,b_{24}\right]$ (3)

$P=\left[p_1,p_2,\cdots ,p_{24}\right]$ (4)

其中W为每小时建筑负荷，V为光伏发电每小时输出电量，B为储能每小时放电量(负值为充电量)，P为每小时电网输入能量。

由功率平衡，有：

$P=W-V-B$ (5)

其中W、V为已知量，因此求解B即可求解P。假设电池容量为Q，采用高倍率充放电池，可实现1C倍率充放，电池剩余电量百分比为SOC，则有以下限定条件：

$\{\begin{array}{l}{\displaystyle {\sum }_{i=1}^{24}{b}_i=0}\\ 0\le b_j\le Q\\ SOC=\frac{Q-{\displaystyle {\sum }_{i=1}^j{b}_i}}{Q}\times 100\\ SOC\in \left(0,100\right]\end{array}$ (6)

其中 $j=1,2,3,\cdots ,24$ 。

以电网准恒功率输出为优化目标，对于储能电池容量不充分的情况下的恒功率取电策略，首先需要制订准恒功率取电达成情况优劣的评判值。设定评判值为：1) 每小时电网取电能量曲线的方差值；2) 每小时电网取电能量曲线平滑度值。两项评判值均以小值为优。

以每小时电网输入能量的方差值为优化目标函数：

$F_1\left(P\right)={\displaystyle {\sum }_{i=1}^{24}{\left(p_i-\bar{p}\right)}^2}$ (7)

其中：

$\bar{p}=\frac{{\displaystyle {\sum }_{i=1}^{24}{p}_i}}{24}$ (8)

优化目标为：

$\min F_1\left(P\right)={\displaystyle {\sum }_{i=1}^{24}{\left(p_i-\bar{p}\right)}^2}$ (9)

以电网每小时电网输入能量的平滑度为优化目标函数，有：

$\min F_2\left(P\right)={\displaystyle {\sum }_{i=1}^{23}\left(p_i-p_{i-1}\right)}$ (10)

同样以最低电价为优化求解目标，假设每小时电价为M：

$M=\left[m_1,m_2,\cdots ,m_{24}\right]$ (11)

优化目标函数为：

$\min F_3\left(P\right)={\displaystyle {\sum }_{i=1}^{24}{p}_i\times m_i}$ (12)

以需求侧响应为优化目标，假设网侧每小时需求能量为：

$G=\left[g_1,g_2,\cdots ,g_{24}\right]$ (13)

则优化目标函数为：

$\min F_4\left(P\right)={\displaystyle {\sum }_{i=1}^{24}\left|p_i-g_i\right|}$ (14)

4. 储能优化策略与控制对象

在恒功率取电模式下，为保证电池储能的可持续性，电池以24小时为周期需充放电平衡，即设定电网恒功率取电值的时候，电池充放电在24小时周期内的净累积量为0。结合建设成本进行综合优化后的储能容量无法满足全天严格恒功率取电要求，需要合理分配储能充放电时间，同时保证：1) 配电网络正常工作状态下，电网取电尽量接近恒功率取电；2) 市电断开后，储能电池可作为备用电源，在足够长的时间内保持不断电；3) 制定合理的控制策略，使控制条件与控制目标得以充分耦合，从而使控制方式合理、得当。恒功率取电对于系统的条件要求为：1) 小时取电能量设定值＝全天负载消耗电能小时平均值：

$p_{set}=\bar{p}$ (15)

2) 储能电池容量≥充放电周期内超出均值能量的累积值:

$Q\ge {\displaystyle {\sum }_{i=1}^{24}\left(p_i^{+}-\bar{p}\right)}$ (16)

储能充足情况下，恒功率取电模式操作方式为：

(17)

即：建筑负荷小时能耗p_i > 恒功率取电设定能耗p_set时，利用电池储能放电补足能耗超出的部分；建筑负荷小时能耗p_i < 恒功率取电设定能耗p_set时，利用电池储能充电补足能耗补足的部分。

储能不足的情况下，同样以24小时作为补偿周期，电池消耗90%为最低SOC值，以留出突发停电下的应急供电。电池充满为补偿满，进行储能充放电策略优化设计。制定3种储能优化策略：

1) 比例充放，即以小时耗电量与小时耗电量成比例补偿：

$b_k=\frac{2Q\left(p_k-\bar{p}\right)}{{\displaystyle {\sum }_{j=1}^{24}\left|\bar{p}-p_j\right|}}$ (18)

其中： $k=1,2,3,\cdots ,24$ 。

2) 平均充放，即每小时放电/充电量相同进行补偿：

$\{\begin{array}{l}{\bar{b}}^{+}=\frac{Q}{length\left(p_k>\bar{p}\right)}\\ {\bar{b}}^{-}=\frac{Q}{length\left(p_k<\bar{p}\right)}\end{array}$ (19)

3) 峰值充放，即只在用电峰值3小时与用电谷值5小时进行放电/充电补偿，其余时间储能电池不充不放。

以上优化策略均基于电网需求输出功率，获取方式分为：1) 恒功率输出，需通过历史数据、能耗变化趋势等预测未来充放电周期内的电网取电平均值；2) 最优电价取电，需得到未来充放电周期内的实时电价及建筑能耗预测值；3) 需求侧响应，需从电力部门获取未来充放电周期内的能耗响应曲线，结合建筑能耗预测值进行最大响应。为达成以上目标，均可选取电网瞬时输出功率作为控制目标，通过下垂控制、变流变压控制等方式实现控制目的。

5. 优化仿真

表1所示为建筑模型仿真参数。

Table 1. Modeling and simulation parameters

表1. 建模仿真参数

采用DeST建筑能耗仿真软件建模，分别得到为每小时建筑负荷W和光伏发电每小时输出电量V冬/夏典型仿真值，其中冬季以上午8点作为周期起始，夏季以上午7点作为周期起始。得到优化前的每小时电网取电量P₀：

$\begin{array}{l}{P}_{0冬}=W_{冬}-V_{冬}=[37.85,75.21,55.05,45.88,48.58,56.14,64.58,47.19,57.38,69.70,48.93,\\ 26.87,25.33,22.62,19.33,8.55,6.70,3.03,3.03,3.03,3.03,3.03,3.03,15.40]\\ P_{0夏}=W_{夏}-V_{夏}=[66.83,70.33,113.40,98.48,78.62,74.79,67.06,69.79,61.02,73.75,93.94,\\ 78.45,42.11,46.36,45.73,44.61,8.64,6.78,3.12,3.12,3.12,3.12,3.12,2.49]\end{array}$

采用比例充放、平均充放和峰谷值充放3种储能充放优化策略，分别对冬/夏季24小时储能充放策略进行优化计算，得到3种储能充放优化策略的电网取电量优化曲线，如图3所示。

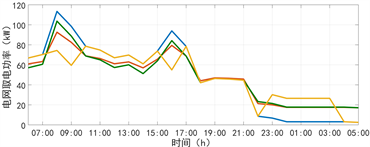a冬季电网取电优化曲线 b夏季电网取电优化曲线

Figure 3. 3 kinds of energy storage and charging optimization strategies optimization curve

图3. 3种储能充放优化策略电网取电量优化曲线

(a) 冬季评判值方差 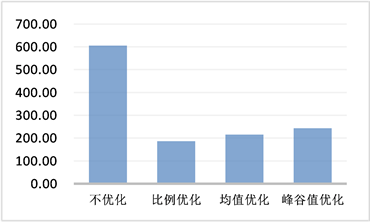(b) 冬季评判值平滑度 (c) 夏季评判值方差 (d) 夏季评判值平滑度

Figure 4. Comparison of evaluation values of 3 kinds of energy storage and charging optimization strategies

图4. 3种储能充放优化策略评判值对比

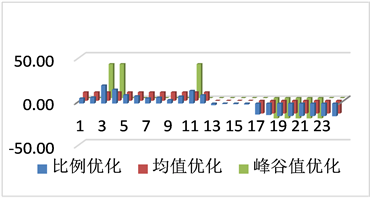(a) 冬季储能24小时充/放电能量 (b) 夏季储能24小时充/放电能量

Figure 5. Winter/Summer 24 hour charge/discharge energy values under 3 optimization strategies

图5. 3种优化策略下的冬/夏季24小时充/放电能量值

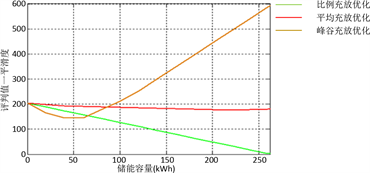
Figure 6. Evaluation values of three optimization strategies and energy storage

图6. 储能对3种优化策略的评判值影响

表2、图4所示为冬/夏季24小时储能充放策略下的能耗曲线评判值对比。由表2、图4知：1) 经比例优化、平均优化与峰谷优化策略优化充放电后，建筑从电网取电量曲线较优化前均表现为方差更小、平滑度评判值更低；2) 3种优化策略在冬/夏季均可以对电网取电曲线的波动进行优化调整；3) 与其他2种优化策略相比，比例优化策略在冬/夏季的曲线方差和曲线平滑度方面均占优。

Table 2. 3 kinds of energy storage and charging optimization strategy evaluation value

表2. 3种储能充放优化策略评判值

如图5所示为3种优化策略下的冬/夏季24小时放电电能值对比。由图5知：1) 比例优化策略按照负荷总需求量进行比例充放电，均值优化策略则按照每小时补偿电量相等的原则对电池进行充放电，而峰谷值优化策略实现了对用电峰值3小时与用电谷值5小时进行放电/充电补偿；2) 峰谷值优化策略充放电量较其他2种优化策略大，这是由于峰谷值时间较短造成，对储能不会造成损害。

以上方式是将储能容量作为固定值进行优化策略的评判值分析，考虑到储能装备的快速发展，以及随着充放电次数的增加，导致储能设备衰减、更换以及扩容等情况，需要对不同储能状态下的优化策略评判值进行计算，以获得1) 储能容量改变对优化策略评判值的影响；2) 不同储能容量下的最优策略。取冬季电网能耗作为研究对象，图6所示为储能变化对3种优化策略的评判值影响。由图6知：1) 建筑储能容量较小时，峰谷充放优化策略对在电网能耗曲线平滑度方面优势明显，但随着储能容量增加，反而呈现负优化效果；2) 绿色曲线所示的比例充放电优化策略，在曲线方差与平滑度2项评判值上均表现较好，并随储能增加，备用能量逐步充沛，表现出良好的优化特性；3) 均值优化仅对方差评判值的改善有良好效果，但对平滑度改善效果不佳；4) 综上可知，提出的3种不同类型的优化策略，在储能严重不足的情况下，选用峰谷充放策略效果较好，在储能较不充足情况下选取比例充放策略进行恒功率输出优化，可得到最优的改善效果。

6. 结论

储能优化策略是研究全直流供电建筑的关键内容。本文以实际建筑为模拟仿真对象，建立结合储能的直流建筑供电模型，计算冬/夏不同工况下的建筑24小时负载能耗模拟值；以直流建筑恒功率取电为研究目标，提出2项评判恒功率取电达成情况的评判值；设计3种不同的优化策略，并比较这几类优化策略在冬/夏不同工况下、不同储能配置情况下的优化策略优劣程度，以指导实际工程方案的设计与实施。

后续应开展的工作主要有：1) 本文比较了几种优化策略在单独实施情况下的优劣性，经综合考量，比例优化策略在储能大小改变、冬夏工况改变时均具有一定的优势，后续可将几种优化策略做有机结合使用，以获取更佳的优化效果；2) 后续需综合变电站建设成本、调峰电站成本与储能造价等建设成本，对最佳储能配置方案做进一步探讨，以期获得更经济的电能配置方案；3) 将储能优化控制策略需要在实际建成后的大厦进行试运行和实际运行，并获得相关运行数据，以验证控制目标与优化控制策略的正确性。

基金项目

中美清洁能源资助项目(编号：2016YFE0102300-03)。