一种光量子非定域性实验方法

An Experimental Method of Optical Quantum Nonlocality

摘要: 为验证和应用光量子的非定域性等特性，类似EPR，提出一个激光脉冲在透明介质界面的反射率计算佯谬，并设计了简明的低预算的激光脉冲与多相介质作用过程记录和分析的实验方法。在对激光脉冲和PMD相机进行同步控制的条件下，该方法对飞行的激光脉冲散射光进行捕捉，原始数据经过图像重构后形成瞬态图像序列。

Abstract: Similar to the EPR paradox, to verify and apply the characteristics of the optical quantum, a problem of the interfacial reflectance to transparent medium is presented, and a low budget concise experimental method for recording and analyzing the process of laser pulse crossing multiphase medium is designed. In this method, the laser pulse and PMD camera are controlled synchronously, scattering laser pulse is captured, and the transient image sequence is formed after the raw data is reconstructed.

1. 引言

非定域性是理论物理中最基本、最尖锐的问题。1935年爱因斯坦等提出的著名的EPR思维实验方法 [1] ，从量子理论推出与“定域性”矛盾的情况：空间距离极大的纠缠粒子对之间，仍然存在不需要时间传输的相互作用。纠缠粒子存在“非定域性”是量子论的一个数学推论 [2] ，并已获多次实验验证。研究人员一直在寻找操纵非定域性的直观而高效的方法。为测量纠缠光子之间的能量/时间量子关联，滑铁卢大学麦克莱恩等 [3] 研究了在非线性晶体上利用激光脉冲产生光子对，然后每对光子被分成两个单独的路径，研究人员配置光敏探测器来测量频率或到达时间。研究小组计算了不同探测器的光子对的数量，发现频率和到达时间的传播与纠缠光子的期望相符，缺点是实验在时间和频率领域都缺乏足够的分辨率。瞬态成像目前依赖飞秒激光器作为光源，以及用于图像捕获的条纹相机 [4] ，其速度快到足以捕捉到飞行的激光画面 [5] ，图1是激光束飞行的瞬态成像序列 [6] 。但是相关设备价格昂贵，达数万美元的设备，且体积庞大、难以操作，目前此类捕获仅在实验室环境中运行。

Figure 1. Transient imaging of laser flight process [6]

图1. 激光飞行过程的瞬态成像 [6]

值得注意的是，文献 [7] 巧妙地对一个PMD相机和激光二极管进行高精度同步控制，找到了一种低费用的(设备总成本只有几千美元)获取脉冲飞行过程相关图像的方法，而且容易操作。图2演示了该方法所提取的瞬态图像。

Figure 2. PMD camera reconstructed transient images [7]

图2. PMD相机同步采集并重构后的瞬态图像序列 [7]

受此启发，本文提出了利用PMD相机和飞秒激光器同步控制进行激光脉冲在介质界面附近传播图像捕捉与分析的费用低廉的实验方法。研究的出发点、理论意义与EPR佯谬、Bell不等式及相关实验类似，并对于光计算、光通信、瞬态成像重构等应用领域具有促进作用。

2. 飞秒激光脉冲在玻璃界面的反射问题

本文提出的实验方案拟搭建一个光量子“非定域性”表达环境，核心问题如图3所示：当飞秒激光的脉冲从光疏介质A (空气)垂直射入长方体状的光密介质B (玻璃)中时，在界面处反射过程是怎样的？如果B的厚度δ是动态变化的，反射率与厚度δ有什么样的关系？如果对于观测区V₁和V₂处进行瞬态Light-in-Flight成像，实验是否可能表现出量子力学中的“非定域性”？

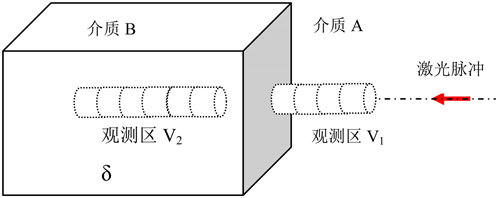
Figure 3. The reflection problem of fem to second laser in glass

图3. 飞秒激光在玻璃界面反射问题

如果将飞秒激光脉冲更换为一般的连续激光束的话，是先后被牛顿和费恩曼研究过的老问题 [8] 。作为量子电动力学的经典案例，费恩曼给出了分析与求解思路，量子力学计算和诸多实验表明，反射率随厚度δ的增加呈现出周期性变化。然而，本文发现这里包含一个重要问题：玻璃厚度δ对于反射率影响是何时开始的呢？是光线传播到玻璃界面的一瞬间就开始了呢，或者之后一会儿才开始呢？是突变还是有一个变化过程呢？

目前已经同时具备两大极其有利的技术进步：① 飞秒激光、② 瞬态成像技术，目前已经具备研究玻璃厚度δ对于反射率瞬时影响的基础，这无疑是有重要的理论意义和应用价值的，但是尚未有将它们用于玻璃界面反射问题进行“非定域性”研究的报道。

3. 实验内容及方法

3.1. 实验场景设计

实验设备包括：① 激光脉冲源；② 玻璃介质；③ 控厚薄膜；④ PMD相机；⑤ 同步器等元器件组成，如图4所示。实验内容主要包括2部分：① 场景设计与实验结果推理；② 数据采集与图像重建。

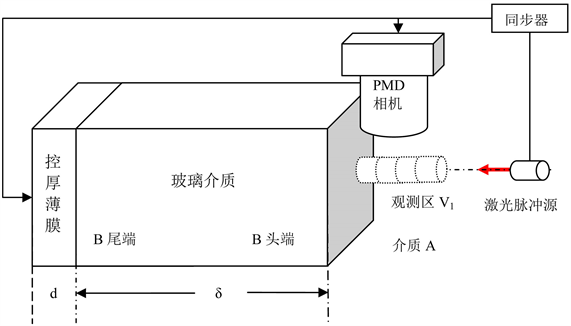
Figure 4. Information non-localized device

图4. 信息非定域性装置

3.2. 实验结果推理

光在玻璃表面的反射率与其厚度有关，从光源S出发到达感光器D的光子可能由2种无法区分的方式发生(经过玻璃下表面反射S à B à D，和经过玻璃上表面反射S à T à D)，接收的光子的概率振幅 $\langle \text{D}|\text{S}\rangle$ 可采用叠加原理求解：

$\langle \text{D}|\text{S}\rangle =\langle \text{D}|\text{B}|\text{S}\rangle +\langle \text{D}|\text{T}|\text{S}\rangle$ (1)

而 $\langle \text{D}|\text{B}|\text{S}\rangle$ 和 $\langle \text{D}|\text{T}|\text{S}\rangle$ 只有相位的不同，该相位差与玻璃厚度δ及光线的波长λ有关，光源S出发到达感光器D的光子的概率的计算公式为：

$\rho ={\left|\langle \text{D}|\text{S}\rangle \right|}^2=\alpha \left(1-\cos \left(\frac{\delta \text{π}}{\lambda }\right)\right)$ (2)

其中，α是与玻璃材料有关的常数。

理论分析表明，无论是连续光或者激光脉冲，甚至是单个光子，在玻璃表明的反射具有以下规律：

1) 玻璃厚度在半波长的奇数倍时，反射率最小，而在波长的整数倍时，反射率最大；

2) 反射率随厚度δ的增加呈现出如图5所示的周期性变化。

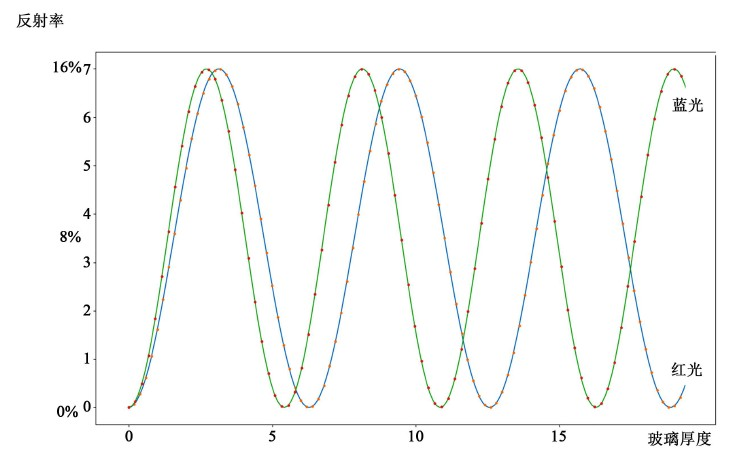
Figure 5. Model of reflection rate variation with medium thickness

图5. 反射率随介质厚度变化模型

本文选取波长为30 nm激光，选取厚度足够且反射率差异很大的2种厚度的介质样品(δ₁ = 90 mm，而δ₂ = 90 mm + 15 nm，使得δ₁的反射率很小而δ₂反射率相对较大，这两种反射状态称为min和max)。

如果采用连续发射激光，上述实验的结果并无悬念。但是飞秒激光的采用，为核实厚度对反射的影响的发生过程的研究提供了重要条件。本文采用30 nm飞秒脉冲分别对于介质样品δ₁和δ₂进行实验，捕捉并分析界面附近脉冲飞行的图像序列。根据前面分析，介质样品δ₁反射率极低，而介质样品δ₂的反射率相对最大。图6是理论分析的实验结果(简称“结果1”)：

Figure 6. Expected result 1

图6. 实验预期结果1示意图

但是，如果是这样就呈现出一个重要的疑惑：在t₂时刻，对于约束在一个很小空间里的激光脉冲来说，它是咋知道玻璃(一个可能占据非常大空间)的厚度(δ₁、δ₂还是其他)的呢？！而通过PMD成像，可以了解这个过程。这个问题是绕不开的，因为假如实验结果就是这样，那么可以利用这样的结果进行设计一个“信息非定域性”佯谬：

理论上，即便厚度非常大，并不会改变min和max这种随厚度变化而周期性变化的规律，正如费恩曼所言：“没有迹象表明这种变化规律会衰减”、“实验上50米厚依然有这种变化规律”。实际上，衰减是没关系的，只要min和max两种状态的区别存在，就可以利用上述装置在B头部和尾部间进行“信息非定域性同步”：存在一些时刻，B尾部插入的薄片(称作尾部操作)实时地被B头部观测区的图像所反映，而δ理论上可以非常大。本方案只是要验证理论结论与实际测量是否冲突，所以不需要很厚的玻璃。这样看来，可能结果1是荒谬的。

图7是另外一种可能的实验结果。在可能结果2中，δ₁在t₁时刻有些反射，而在t₂后反射区域消失。这种情况可以没有“信息非定域性”佯谬。但是如果这样的话，利用PMD相机成像并进行分析，可以观测到一团存在的东西(光)在飞行过程中突然在一个区域里消失，不也是“光量子非定域性”佯谬吗？！

Figure 7. Expected result 2

图7. 实验预期结果2示意图

3.3. 数据采集与图像重建

直接用瞬态成像完成上述实验，主要缺点是费用太高。本文设计采用PMD相机同步采集并重构，得到瞬态图像序列。对于课题的物理学目的，两者是等价的，后者不仅便宜，且更具有实用价值。主要工作如下：

① 基于PMD相机各个感光单元可以对输入的不同阶段的光子进行积分的功能，对于PMD相机进行硬件编程并提供灵活的模式选择指令。

② 基于飞秒激光器调制功能，动态调制飞秒激光脉冲的脉冲数及相位。

③ 研制PMD相机和飞秒激光器的同步器。

④ 最后，通过同步器对于PMD相机和飞秒激光器进行控制，采集初始图像数据，并对这些数据进行清理、时间对齐、平滑和视频输出等处理。

4. 结论

本文从一个经典的玻璃反射问题里，延伸提出了飞秒激光的玻璃反射问题。提出一种操纵非定域性的直观而高效方法，分析了实验方案所要解决的主要问题和研究内容，为建立飞秒激光脉冲在透明光密介质界面反射过程模型、建立PMD相机和飞秒激光器的同步控制方法及相关的瞬态成像方法提供了新思路。

本文通过同步器对于PMD相机和飞秒激光器进行控制，在一个区域(玻璃的上表面)获取空间分离的另外一个区域(玻璃的下表面)发生的厚度变化信息，而这种信息的传播理论上是不需要时间的。飞秒激光和PMD相机为该实验提供了巧妙的帮助。

光子飞行过程中所捕获的图像和飞行中的光子分布之间的关系是量子力学里的一个基本问题：像和实在之间的关系。量子力学代表人波尔等认为：如果观测到了，那么它就在这里；不观测，不仅不能说它在这里，也不能说它存在。也许有个更容易接受的、甚至跟量子力学有所不同的理解：没有“非定域性”，但是有许多新的其他东西。

基金项目

感谢武汉科技大学大学生科技创新基金资助项目(项目编号：17ZRA099)。