1. 引言
GNI,即国民总收入(Gross National Income),是指“一国经济总体当期从国内生产和国外生产中获得的生产性收入总量”,是该经济体所有常住单位在一定时期内收入初次分配的最终结果。GNI等于GDP加上来自国外的净要素收入,一般来说来自国外的要素净收入远小于本国GDP的规模,因此GNI与GDP往往规模相当,二者都被用于反映一国的经济规模,见(蒋萍,2011 [1] ;侯瑜,2012 [2] )。因此,科学、准确地对人均GNI做出预测为政府部门有效的调控经济政策和制定发展规划有着重要的作用。
鉴于GDP在经济分析与政策制定中的重要性,GDP数据质量历来备受关注,国内外很多文献从不同角度、使用不同方法对GDP数据预测做了大量研究工作。侯青霞 [3] 利用线性自回归模型和函数系数自回归模型对我国人均GDP进行建模预测,张雅清 [4] 运用GM(1,1)模型对山西省人均GDP进行模拟预测,并用残差修正的GM(1,1)模型对预测进行改进,王永杰 [5] 采用神经网络算法对GDP和CPI进行预测,并提出了PCA-PSO-BP模型。其中GM(1,1)模型对“小样本、贫信息”系统具有良好的预测效果。然而,经典GM(1,1)模型对原始数据只进行一阶累加,导致模型的自由度较小。为此,沈燕与张丽玲 [6] 将复化Simpson引入到灰色模型中,详细讨论了模型的性质并给出了详尽的数值计算实例。
本文在上述研究的基础上,通过复化Simpson改进了灰色模型的背景值,利用神经网络能够逼近任意函数的优点,将影响GNI发展的12种因素(第一产业、第二产业、第三产业、农林牧渔、工业、建筑、批发零售、交通运输、住宿和餐饮、金融、房地产、人均国内生产总值)作为神经网络的输入,将复化Simpson改进的GM(1,1),CSGM(1,1))与BP神经网络进行误差最小线性加权组合,利用遗传算法能够智能寻优的特点,求得最优权系数,并对我国国民总收入进行了预测研究。从中国统计年鉴获得的1987年~2007年的我国国民总收入数据作为建模数据,2008~2016年的数据作为模型的检验数据,对比分析GM(1,1)模型、CSGM(1,1)模型、BP神经网络模型、复化Simpson公式改进的灰色神经网络模型的预测精度。
2. 研究方法
2.1. GM(1,1)预测模型
设原始序列
为非负原始序列:
,对于满足光滑条件序列,可建立灰色微分方程。经过累加生成
,称
为
的1-AGO序列:
,其中:
(1)
为
的紧邻均值生成序列:
,其中:
(2)
为此,灰微分方程为:
(3)
其中,a发展系数,b为灰色作用量。若
为参数列,且有:
(4)
则式(3)的最小二乘估计参数满足:
(5)
若
满足式(4)和式(5),相应的白化微分方程为
(6)
则,GM(1,1)模型的时间序列为:
(7)
还原后,
的预测值为:
(8)
2.2. 背景值误差产生分析
由原始GM(1,1)的还原时间响应序列知,GM(1,1)预测模型的精度取决于参数a,b,然而决定参数a,
b,的是
,因此GM(1,1)模型误差主要来源于
的计算。对
在
进行积分,有:
(9)
式(9)联合
,有:
(10)
GM(1,1)模型的背景值的几何意义如图所示,可以明显看出,曲线
在区间
上与横轴t所围成的曲边梯形的面积即是GM(1,1)模型的背景值。传统计算
的方式是计算梯形的面积,如图1所示。而用复化Simpson公式计算的GM(1,1)模型,背景值是区间
上的曲边梯形的面积,如图2所示。可以看出,其计算产生的误差明显小于传统的计算方式。
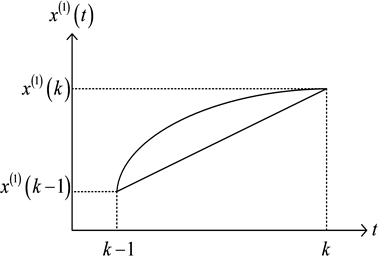
Figure 1. Comparison between the real value and the trapezoid formula background value
图1. 标准试验系统结果曲线
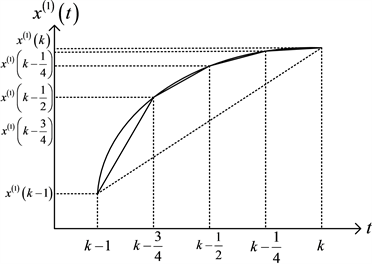
Figure 2. Comparison of the true value and the background value of complex Simpson formula
图2. 真实值与复化Simpson公式的背景值的比较
2.3. 基于复化Simpson公式改进的GM(1,1)模型
由于在使用复化Simpson积分公式时需要知道在每一个小区间内的插入分点所对应的值,所以在此引入1-AGO动态序列预测模型 [7] ,从其他学者的研究成果可知,1-AGO序列成非齐次指数形式,这条曲线只是一条近似曲线。故可以使用这条曲线构造小区间端点值的一个动态序列模型。由此,记
,则可以求出每个区间
上n等分点处的函数值(即
的值),然后利用复化Simpson求积公式计算出优化的背景值。设非负原始数据序列为
令其1-AGO累加序列为:
,则有:
(11)
(12)
(13)
称
为其1-AGO动态序列预测模型。
记积分区间为
,将区间等分成
份,各节点为
(14)
则考虑(15)式在
上的积分,有
(15)
式(15)可进一步表示为:
(16)
结合1-AGO动态序列预测模型,运用数值积分方法中的复化Simpson积分公式,计算
在
上的积分,有:
(17)
则(15)式可表示为:
(18)
对比(16)式得背景值
为:
(19)
进一步化简(18)式有:
(20)
记
为参数列,由最小二乘法原理知,参数列需满足:
(21)
其中:
,
(22)
2.4. BP神经网络
BP (back-propagation)神经网络是由Rumelhard等科学家于20世纪80年代提出的,BP神经网络是一种按误差反向传播算法训练的多层前馈网络,也是目前应用最广泛的神经网络模型之一。BP神经网络具有很强的非线性映射能力,并且网络的隐含层数、各层的处理单元数及网络的学习系数等参数可根据问题的具体情况而设定,具有很高的灵活性,因此被应用到很多领域。图3展示了BP神经网络的简单结构拓扑图:
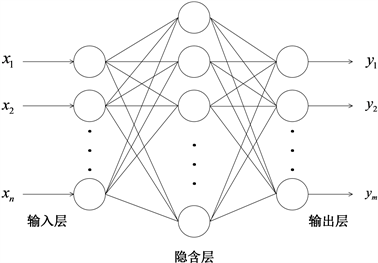
Figure 3. BP network structure topology diagram
图3. BP网络结构拓扑图
2.4.1. 神经元模型
一个基本的BP神经元模型具有R个输入,每个输入对应一个权值w,加权后与下一层连接。网络输出可表示为:
(23)
其中为f为输入层与输出层的传递函数,w代表权值,b为隐含层神经元的偏置值。
2.4.2. 激励函数
BP神经网络的功能的不同主要取决于激励函数的不同,激励函数选择的多样性使得神经网络有了不同的信息处理能力。神经元输入层与输出层之间的关系由激励函数f决定。神经网络的激励函数有多种,本文使用的激励函数为S型函数,其表达式为:
(24)
2.4.3. BP神经网络的学习算法
网络的学习算法分成正向传播和反向传播两部分。在正向传播过程中,每一层神经元只影响下一层神经元。首先输入样本数据作为训练数据,将输入数据传送至各个神经元,经隐含层计算处理后,输出层输出对应的预测值。如果预测值与实际值的误差较大,则进入学习算法的第二部分,输出层进行反向传播该误差,沿原路返回并逐层调整各层权值,不断降低误差,直至误差精度满足我们的要求。学习算法的核心思想是梯度下降法。设一样本
,
,
,隐含层神经元为
。输出层与隐含层神经元间的权值矩阵
和隐含层与输出层神经元之间的网络权值
分别为:
(25)
(26)
则隐含层神经元的输出为:
(27)
其中:
(28)
为隐含层传递函数。
输出神经元的输出为:
(29)
其中:
(30)
为输出层传递函数。
网络输出与期望输出的误差为:
(31)
网络的训练误差是各层
和
权值的调整值,调整权值可改变误差E,调整的数学表达式如下:
(32)
(33)
式(32)、(33)中负号表明梯度下降,
是常数,反应了学习过程中的学习梯度。
2.5. 复化Simpson神经网络组合预测模型
预测精度是评价一个预测模型好坏的核心指标。在实际预测中,由于系统复杂,随机或不确定因素较多,单一预测模型对系统的考虑较少,往往不能很好的反映系统的发展过程,预测存在一定的缺陷。但不同的单一预测模型考虑了系统不同的因素,把它们设法进行优化组合,综合考虑单一预测模型有用的信息,能从各个方面提现系统的发展变化。在将单一预测模型进行组合时,由不同的方法推导加权系数,能得到多种不同的组合预测模型。本文采用最优线性组合方式,其基本思想就是根据某种准则构造相应的目标函数,在有关约束条件下求得目标函数的最值,从而得到最优的组合加权系数,最终得到优化组合预测模型。
本文建立的GM(1,1)模型只适用于中短期的预测,而且数据要求呈指数增长规律。BP神经网络则需要大量的数据样本进行训练,而且学习时间长。本文综合考虑了单一预测模型的不足,将CSGM(1,1)模型和BP神经网络模型通过线性最优加权组合的方式,以误差平方和最小为目标函数,使用智能算法—遗传算法来求解确定最优组合的权系数,进行优化组合以达到提高预测精度的目的。组合结构如图4所示:
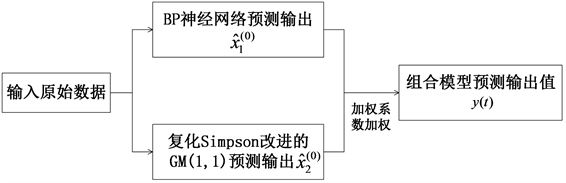
Figure 4. BP network structure topology diagram
图4. BP网络结构拓扑图
令
,
,
分别表示BP神经网络模型、复化Simpson公式改进的GM(1,1)模型和组合预测模型在t时刻的预测输出值,
,
为BP神经网络模型、复化Simpson公式改进的GM(1,1)模型的组合权系数,则:
(34)
且
,
满足
(35)
令
,
,
分别为BP神经网络模型、CSGM(1,1)模型、组合预测模型在t时刻的误差,则:
(36)
令
,即误差绝对值平方和,进一步表示为:
(37)
由最小二乘法的思想,对
中的
,
分别求偏导数有:
(38)
令:
(39)
(40)
则上式方程组表示成矩阵形式有:
(41)
由于为非线性最小二乘问题,若用经典的求解非线性问题的算法,此处求解非常复杂。故本文使用智能算法—遗传算法来求解(38)式,以此来求得最终的组合预测模型的权系数
,
。
遗传算法(Genetic Algorithm)是Holland在1975年提出的一种借鉴生物界的进化规律演化而来的有效解决最优化问题的自适应全局优化搜索算法。遗传算法能有效的解决多峰函数优化、多目标问题以及非线性问题等。遗传算法将问题求解转化成“染色体”,即用编码表示字符串。遗传算法从一群染色体出发,不断的交叉变异,产生新的子代,同时算法将更优的个体保留下来,随着算法的不断进行从而产生更好的个体。与传统的优化算法相比,遗传算法可以有效避免许多求解障碍,直接以目标函数值作为搜索信息。具有自组织、自适应和自学习性等特点。本文以(38)式为目标函数,运用遗传算法进行寻优求解,以得到最优权系数,以此来构建最优组合预测模型。
3. 我国国民总收入预测
为了对上述模型的适用性进行验证,本文从中国统计年鉴选取影响我国1978~2016年的国民总收入的12个相关因素(第一产业、第二产业、第三产业、农林牧渔、工业、建筑、批发零售、交通运输、住宿和餐饮、金融、房地产、人均国内生产总值)。利用GM(1,1)和复化Simpson改进的GM(1,1)对我国国民总收入进行建模预测。使用1978—2007年的相关数据作为神经网络的输入层,国民总收入作为目标输出,以此对我国国民总收入进行建模预测。最后将复化Simpson改进的GM(1,1)的预测值与BP神经网络的预测值进行组合,得到组合模型的预测值。使用2008—2016年的数据作为验证数据检验模型的误差精度。相关数据见表1:

Table 1. Actual GNI data from 2008 to 2016
表1. 2008~2016年的GNI实际数据
4. 预测结果
本文利用MATLAB编程计算,分别求得GM(1,1)模型、复化Simpson公式改进的GM(1,1)模型、BP神经网络模型建立预测模型的预测值。利用遗传算法,得到BP与复化Simpson改进的GM(1,1)模型的组合权系数分别为
,
,由此建立出复化Simpson公式改进的灰色神经网络组合模型:
。4种模型的预测值见表2和图5。从表2和图5中可看出,所建立的GM(1,1)模型的预测结果相对较差,CSGM(1,1)模型和BP神经网络对GNI预测结果相对GM(1,1)的预测值有一定的改进,能反映出2008年到2016年GNI的变化趋势。然而,复化Simpson公式改进的灰色神经网络组合模型的预测值比其他模型更接近真实值。

Table 2. Comparison of the predicted and actual GNI values of China from 2008 to 2016 based on different models
表2. 基于不同模型的中国2008~2016年GNI预测值与实际值的比较
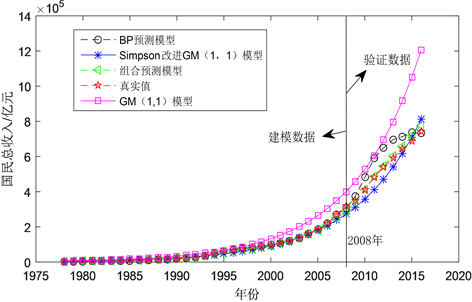
Figure 5. Comparison of predicted and actual GNI values of China from 1978 to 2016 based on different models
图5. 基于不同模型的中国1978~2016年GNI预测值与实际值的比较
为了比较GM(1,1),CSGM(1,1),BP,复化Simpson公式改进的灰色神经网络组合模型的预测精度,分别计算4种模型验证数据的RMSPEPO以及相对误差,其结果见表3。此外,为了更直观的比较4种模型的预测精度,图6给出了4种模型的相对误差。

Table 3. Relative error between predicted and actual GNI of per capita based on different models
表3. 基于不同模型的人均GNI预测值与实际值相对误差
从表3、图5可看出,GM(1,1)的RMSPEPO高达38.8671%,CSGM(1,1)模型的RMSPEPO为10.9451%,BP神经网络模型的RMSPEPO为13.9508%,复化Simpson公式改进的灰色神经网络组合模型的RMSPEPO为4.4687%。因此,计算结果表明,复化Simpson公式改进的灰色神经网络组合模型对GNI的预测结果优于GM(1,1)模型,复化Simpson改进的GM(1,1)模型,BP神经网络模型。
5. 结论
本文利用Simpson积分公式对GM(1,1)模型的背景值进行改进,再将其与BP神经网络模型组合,建立复化Simpson公式改进的灰色神经网络组合模型对中国国民总收入(GNI)进行预测分析,其结果表明:
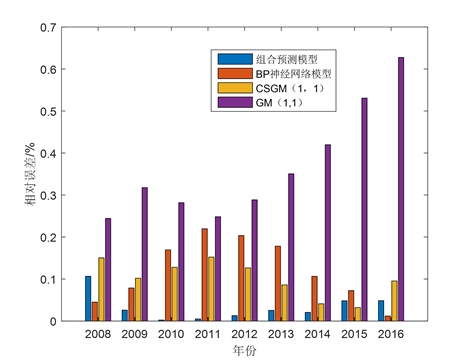
Figure 6. GNI relative error comparison graphs based on different models in verified data
图6. 基于验证数据中不同模型的GNI相对误差对比图
1) 复化Simpson公式改进的灰色神经网络组合模型用于中国国民总收入(GNI)的方法是切实有效的。
2) 复化Simpson公式改进的灰色神经网络组合模型预测的精度最高,RMSPEPO为4.4687%。其预测精度高于GM(1,1)模型、BP神经网络模型和复化Simpson改进的GM(1,1)模型。
3) 组合预测的预测精度比单个预测精度更高。同时,它可以克服单一模型预测的欠缺,综合结合各种预测模型的长处,能够更好地降低预测的误差。因此,组合预测模型可以达到改观单一预测结果的目的。进一步期望本文模型能应用于人口、能源等领域。
基金项目
西南科技大学理学院创新基金项目“基于scrapy的房地产数据爬虫系统” (项目编号:LXCX-19),主持人:杨羿轩。