基于分位数自回归模型的健康险保费收入研究

Study on the Health Insurance Premiums Income Based on Quartile Autoregression Model

摘要: 健康险保费收入是度量健康保险业发展情况的关键经济指标。本文结合分位数回归方法对我国1991年1月~2017年6月健康险保费收入的时序数据建模：首先识别了AR(3)模型，之后运用分位数回归方法建立分位数自回归模型，并较准确地拟合出原数据的增减趋势，最后用自回归AR(3)模型和分位数自回归QAR(3)模型分别做短期预测，基于多个评价指标比较两种模型预测效果，结果表明分位数自回归模型预测效果更好。

Abstract: Health insurance premium income is a key economic indicator to measure the development of health insurance industry. In this paper, the time series data of health insurance premium income from January 1991 to June 2017 were modeled with the quantile regression method. Firstly, the model AR(3) was identified, and then the quantile autoregressive model was established by the method of quantile regression, and the increase and decrease trend of the original data was fitted accurately. Finally, the short-term prediction is made by autoregressive AR(3) model and quantile autoregressive QAR(3) model respectively. The prediction results of the two models were compared based on several evaluation indicators. The results show that the quantile autoregressive model is more effective.

1. 引言

我国的健康保险业务自上世纪80年代恢复以来，得到了快速的发展，根据中国保监会发布的健康保险保费收入数据，我国健康保险保收入由1999年的3.65亿多元增加到2017年的4389.4亿多元，期间平均每年增长约为34.16%。在新时代背景下，健康与养老服务业已逐渐成为我国新的经济增长点和扩大内需的着力点，我国健康保险的发展也面临着更多新的挑战。国家和保险业需要根据健康保险的现状及时做出相应的措施和调整战略。

Koenker和Bassett (1978) [1] 提出的分位数回归是最小二乘回归方法的优化 [2] 。与普通的均值回归相比，分位数回归能精细地刻画自变量对于响应变量对应于不同分位点的不同影响。将分位数回归模型与时间序列分析结合能较好地提高模型的预测能力和实用性 [1] [2] [3] [4] 。彭良玉等(2011)对分位数回归和时间序列理论进行了深入研究，并在此基础上分析了澳大利亚月度红酒销量数据，认为与时间序列模型相比，分位数回归方法能够得到更加完整的红酒销量信息 [3] 。盛选义等(2012)将分位数回归方法应用到时间序列系数求解中，分析我国对外贸易总额数据，实例验证结果表明模型预测效果较好且具有一定的应变能力 [4] 。崔丙维(2013)根据时间序列的一般理论识别了AR模型，然后按照将所得模型结合分位数回归的思路，建立了分位数自回归模型，还将此模型应用到考察风速变化的实际问题中，结果显示用分位数回归模型进行拟合能有更高的拟合度 [5] 。本文拟运用分位数自回归(QAR)模型研究健康险保费收入的预测问题。

2. 实证分析

本文对我国健康保险保费收入实际数据进行分析，为了更全面且准确地探究我国健康险保费收入的情况，从国泰安数据库 [6] 选用了1999年1月到2018年2月我国的健康险保费收入数据，这是官方发布的有记录以来的所有数据。将原始数据分为两个部分，1999年1月直至2017年6月的保费收入数据组成第一部分，作为建立模型的依据，剩余的2017年7月至2018年2月的健康险保费收入共8个数据用来检验模型预测效果。

2.1. 数据预处理

图1为我国健康险保费收入时间序列图。可以看出该序列值基本是逐年增加但近年的最高值与最低值差距较大。图2为健康保险保费收入时间序列的分解图。可以看出序列不仅具有逐年增加的趋向，而且所显示出来的季节性也不可忽视。从而可以判断该序列是非平稳的，因此在建模之前要进行必要的预处理以使其稳定。

由于选用的是月度数据，尝试对原序列进行1阶12步差分，差分后序列显示均值平稳但在序列后面部分方差较大，如图3所示，这是序列存在异方差才会表现的特点。为了进一步确认序列是否真的存在异方差性，考察1阶12步差分后序列残差平方图的方法，所得结果如图4所示，可以看到图中曲线后部的差异更加显而易见，因此得出残差序列存在异方差的结论。

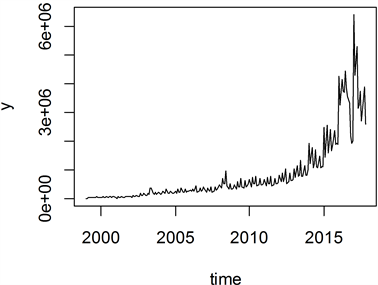
Figure 1. Time series chart of China’s health insurance premium income

图1. 我国健康险保费收入时序图

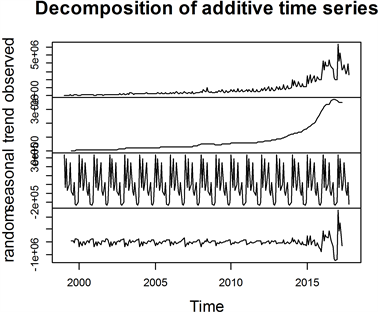
Figure 2. Data decomposition map of China’s health insurance premium income

图2. 我国健康保险保费收入数据分解图

Figure 3. Time series diagram of the 1st order 12-step difference graph

图3. 1阶12步差分后时序图

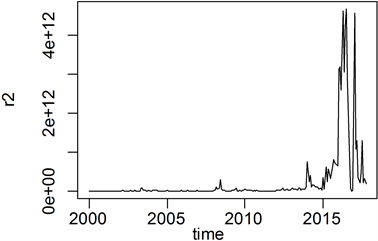
Figure 4. 1st order 12-step difference residual squared graph

图4. 1阶12步差分后残差平方图

下面通过对数变换来消除序列的异方差性。图5是经过对数变换的序列1阶12步差分后的时间序列图。图中曲线大致上是在一个常数值附近进行无规律的变动，并且波动没有离开该常数很远。按照时间序列图检验法的规则可以认为处理后的序列已经平稳。但仅根据时序图判断序列平稳性存在一定的主观因素，为了得到更加客观的结果，接下来使用单位根法检验处理后的时间序列的平稳性，该检验得到的p值是0.04354，显然在显著性水平取 $\alpha$ 的值是0.05时拒绝原假设，所以单位根检验法得到的结果同样证实了差分后序列是平稳的。

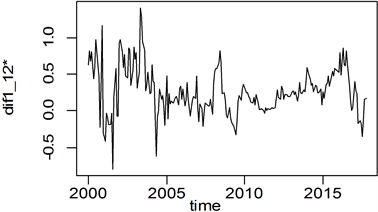
Figure 5. Time-series sequence of 1st order 12-step difference after logarithmic transformation

图5. 经过对数变换的序列1阶12步差分后时序图

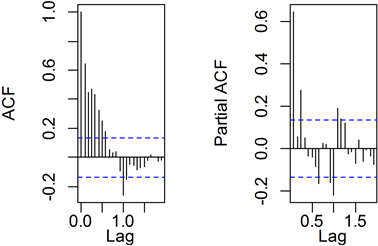
Figure 6. Autocorrelation coefficient and partial autocorrelation coefficient of pre-processed sequence

图6. 预处理后序列的自相关系数及偏自相关系数图

2.2. 平稳序列的白噪声检验

经过预处理之后所得序列已经平稳，下一步对平稳序列进行纯随机性检验。采用Q_LB检验统计量做平稳序列的白噪声检验，结果见表1。

Table 1. Parameter table of white noise test

表1. 白噪声检验参数表

如表1中的结果显示，延迟6期延迟12期的Q_LB统计量对应的p值都远小于显著性水平，可以判定差分后序列为非白噪声序列，即该序列中隐含着有用信息，有必要继续对此序列做进一步分析建模。

2.3. 模型识别

按照前文预处理后得到的平稳序列，其样本自相关及偏自相关图如图6所示，显然图6中显示的样本自相关图具有拖尾的特点，而偏自相关图则是三阶截尾，根据模型定阶准则初步认为选择AR(3)模型是最合理的。但是这里可以选择的模型并不只有AR(3)一个，还存在其他有效的模型，本文根据AIC准则判断最优模型，计算各个有效模型的AIC函数值，所得结果如表2所示。

Table 2. AIC values for each valid model

表2. 各个有效模型的AIC值

依据AIC函数值最小对应的模型即为最优的判断标准，比较表2中每一个模型的AIC函数值可以确认选用AR(3)模型是最恰当的，与按照ARMA模型定阶原则得到的模型一致。AR(3)模型形式如式(2-1)所示。

$y_t={\beta }_0+{\beta }_1{y}_{t-1}+{\beta }_2{y}_{t-2}+{\beta }_3{y}_{t-3}+{\epsilon }_t$ . (2-1)

由于后面会比较时间序列的自回归模型和时间序列分位数回归模型的预测效果，所以这里用最小二乘估计方法，计算了AR(3)模型的参数，结果如式(2-2)。

$y_t=0.06052+0.57761y_{t-1}-0.1085y_{t-2}+0.28558y_{t-3}+{\epsilon }_t$ . (2-2)

Table 3. Results of the t-test of the parameters

表3. 参数t检验结果

表3给出了对AR(3)模型系数的t检验结果，可以看到所有系数的p值都小于显著性水平0.05，也就是说当期的健康保险保费收入受其前三期的健康险保费收入影响，并且影响是显著的。

2.4. 分位数回归

将分位数回归运用到自回归AR(3)模型上来，首先要选择合适的分位数，在实际应用中，中位数( $\tau =0.5$ )有着非常重要的作用，常常和均值共同反映样本数据所包含的位置信息。此外，中位数的取值是由其在所有标志值中所处位置所决定的，不受分布数列极值的影响，相对于均值来说，中位数在一定程度上提高了对样本分布数列的代表性；当少数误差数据严重偏离真实数据时，会导致样本均值大受影响，而丝毫不会影响中位数 [7] 。所以本文选取5个分位数 $\tau =0.05,0.15,0.5,0.85,0.95$ ，其中 $\tau =0.5$ 的分位线即为中位数回归，为后文的点预测(主要指中位数回归预测)和区间预测( $\tau =\left(0.05,0.95\right)$ 表示 $\tau =0.05$ 预测区间， $\tau =\left(0.15,0.85\right)$ 表示 $\tau =0.15$ 预测区间)奠定基础。

估计不同分位点条件下模型的系数 ${\beta }_{\text{0}},{\beta }_{\text{1}},{\beta }_{\text{2}},{\beta }_3$ ，得到系数的估计值如表4所示。观察表4可知不同的分位点所对应的系数不同，得到了时间序列分位数回归模型(QAR)。

Table 4. Estimates of coefficients of models corresponding to different quantiles

表4. 不同分位点对应的AR(3)系数估计值

以中位数回归模型为例，健康险保费收入在t时刻拟合的分位数自回归模型(QAR)为：

$Q_{0.5}\left(y_t|F_{t-1}\right)=0.03036+0.70617y_{t-1}-0.03864y_{t-2}+0.18706y_{t-3}$ . (2-3)

其中 $F_{t-1}$ 表示 $y_t$ 的滞后项产生的σ-域，这里 $F_{t-1}=\left\{y_{t-1},y_{t-2},y_{t-3}\right\}$ 。

对分位点与模型的系数进行研究。图7描述的是模型各系数随分位数变化而产生相应变化的情况，即对AR(3)模型实施分位数回归分析后得到的结果，图7中的黑色虚线是在不同的分位点处各参数的回归系数，灰色形成的阴影范围为估计值的95%置信区间带 [1] 。而红色的三条平行线中，实线是最小二乘法所得的参数估计值而虚线则是其95%的置信区间上下限。

根据自回归模型 $y_t={\beta }_0+{\beta }_1{y}_{t-1}+{\beta }_2{y}_{t-2}+{\beta }_3{y}_{t-3}+{\epsilon }_t$ 可知，图7中第一个图的纵坐标为常数项 ${\beta }_{\text{0}}$ 的估计值，第二个图的纵坐标为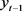的系数 ${\beta }_{\text{1}}$ 的估计值，第三个图的纵坐标为 $y_{t-2}$ 的系数 ${\beta }_{\text{2}}$ 的估计值，第四个图的纵坐标则是 $y_{t-3}$ 的系数 ${\beta }_{\text{3}}$ 的估计值。分位数刚开始上升时，参数 ${\beta }_{\text{1}}$ 的估计值先存在小段下降的情况而后逐渐上升。也就是说，当健康保险发展低迷时，对于经过对数转换和差分后的数据，前一期对后一期的影响会随这分位数的增加而减少，而在正常发展水平下，前后两期数据之间的影响随着分位数的增加而增加。而参数 ${\beta }_{\text{2}}$ 随着分位数的增加其先增加然后持续平稳而后下降，说明只有在健康保险发展很不好时，分位数增加 $y_{t-2}$ 对 $y_t$ 的影响是正向的，或者健康保险收入走高， $y_{t-2}$ 对 $y_t$ 的影响则是分位数增加而下降。再看参数 ${\beta }_{\text{3}}$ ，其与分位数之间的关系则较为简单，分位数逐渐增加 ${\beta }_{\text{3}}$ 大体也是上升的趋势，即 $y_{t-3}$ 对 $y_t$ 的影响会随着分位数的增加而变大。

根据已得出参数估计值的时间序列分位数回归模型，作不同分位点条件下的模型拟合图如图8所示。图中上下两条红色线分别代表0.95和0.05分位点条件下的拟合值，绿色线由上往下分别代表0.85和0.15分位点条件下的拟合值，蓝色线则代表0.5分位点条件下的拟合值，黑色线为经过预处理的数据。从整

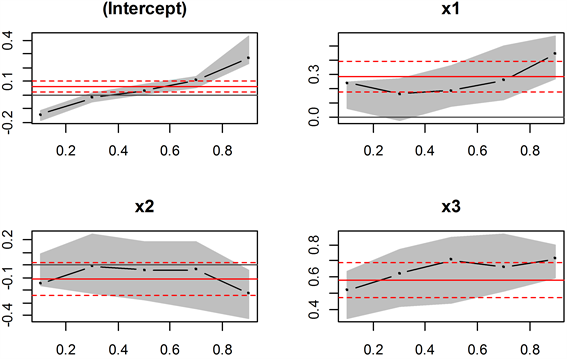
Figure 7. Trends and confidence intervals for model parameters

图7. 模型参数的变化趋势及置信区间

体图可以看出，基于时间序列的分位数回归模型的拟合结果均能合理的反映出健康险保费收入的变化规律，此外中位数( $\tau =0.5$ )的分位数曲线与真实健康险保费收入的值最为接近，这与分位数回归的概念相符。

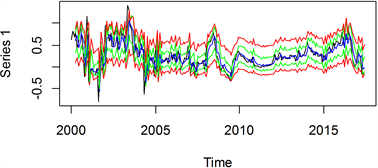
Figure 8. Quantile autoregressive model fitting effect diagram

图8. 分位数自回归模型拟合效果图

2.5. 序列预测

利用最小二乘法和分位数回归估计得到的模型预测2017年7月到2018年2月的健康险保费收入。为了更好比较预测效果，表中给出了2017年7月到2018年2月的实际观测值，得到的健康险保费收入预测值如表5所示。

Table 5. Predicted value of health insurance premium income (ten thousand yuan)

表5. 健康险保费收入预测值(万元)

判断模型点预测效果的模型评价指标有 [7] ：

1) 根均方误差 $\text{RMSE}(\tau )$

$\text{RMSE}\left(\tau \right)=\sqrt{\frac{1}{T}{\displaystyle \underset{t=1}{\overset{T}{\sum }}{\left(y_t-{\hat{Q}}_{\tau }\left(y_t|F_{t-1}\right)\right)}^2}}$ ． (2-4)

2) 平均绝对误差 $\text{MAE}(\tau )$

$\text{MAE}\left(\tau \right)=\frac{1}{T}{\displaystyle \underset{t=1}{\overset{T}{\sum }}\left|y_t-{\hat{Q}}_{\tau }\left(y_t|F_{t-1}\right)\right|}$ . (2-5)

3) 平均百分比误差 $\text{MAPE}(\tau )$

$\text{MAPE}\left(\tau \right)=\frac{1}{T}{\displaystyle \underset{t=1}{\overset{T}{\sum }}\left|\frac{y_t-{\hat{Q}}_{\tau }\left(y_t|F_{t-1}\right)}{y_t}\right|}\times 100\%$ . (2-6)

其中，T是预测值的个数， $Y_t$ 表示实际观测的数据， ${\hat{Y}}_t$ 表示用模型所得的预测值， $F_{t-1}$ 表示 $y_t$ 的各阶滞后变量生成的σ-域。表6列出了自回归模型(AR)、分位数自回归模型(QAR)对健康险保费收入数据点预测( $\tau =0.5$ )下的预测值的效果比较情况。显然QAR模型相对于AR模型在预测效果上有了显著提高，QAR模型的RMSE提升了38.7%、MAE提升了35.8%，MAPE更为显著提升了43.9%，同时可以说明简单地运用均值回归模型对数据进行预测缺乏合理有效性。

Table 6. Comparison of point prediction results

表6. 点预测效果比较

进一步考察区间预测的效果，评价指标有 $\text{FICP}\left(\tau \right)$ [7] ，它是指实际值落在预测区间的概率。

$\text{FICP}\left(\tau \right)=\frac{1}{T}{\displaystyle \underset{t=1}{\overset{T}{\sum }}{I}_t\left(\tau \right)}\times 100\%,\tau \in \left(0,0.5\right)$ . (2-7)

其中 $I_t\left(\tau \right)$ 为Boolean变量，当 $Y_t$ 落入其预测区间 $\left[{\hat{Q}}_{\tau }\left(y_t|F_{t-1}\right),{\hat{Q}}_{1-\tau }\left(y_t|F_{t-1}\right)\right]$ 时， $I_t\left(\tau \right)=1$ ，否则 $I_t\left(\tau \right)=0$ 。根据表5，2017年7月至2018年2月的8个实际值，仅有2017年7月的真实值未落入 $\tau =0.05$ 及 $\tau =0.15$ 预测区间， $\tau =0.05$ 及 $\tau =0.15$ 预测区间内的覆盖率达到了87.5%，说明分位数自回归模型区间预测的效果较好。

3. 结论

本文按照通常的时间序列分析方法对数据建模之后，在选定分位数的条件下获得时间序列分位数回归模型，并以此模型进行参数估计和预测，主要将这个方法应用于我国健康险保费收入的研究中。采用1999年1月到2017年6月我国健康保险保费收入进行建模，识别得到AR(3)模型，从选定的模型看，我国健康险当月的保费收入会受此前三个月保费收入的影响。一方面可以理解为健康险保费收入存在延展性，这是因为长期健康保险保单一般会有分期缴纳的保费，所以保费收入会表现出一定的滞后效应；另一方面保险公司可以优化健康保险的市场格局，升级产品结构，从而增强自身竞争力寻求发展。

根据时间序列分位数回归模型进行拟合，拟合结果能合理地反映出健康险保费收入的变化规律，此外中位数( $\tau =0.5$ )的分位数曲线与实际健康险保费收入的值最为接近，这与分位数回归的概念相符，也说明用 $\tau =0.5$ 的模型进行点预测的合理性。用AR(3)模型和时间序列分位数回归模型分别预测了2017年7月到2018年2月的健康险保费收入，分位数自回归(QAR)模型的点预测效果相对于自回归(AR)模型有了显著提高，QAR模型的根均方误差RMSE提升了38.7%、平均绝对误差MAE提升了35.8%，平均百分比误差MAPE更为显著提升了43.9%，显然分位数条件下的自回归模型的点预测效果比用时间序列模型所得的效果要好得多。最后还考察了区间预测的效果， $\tau =0.05$ 及 $\tau =0.15$ 预测区间内的覆盖率达到了87.5%，表明分位数自回归模型区间预测的效果较好。经过对健康险保费收入的实证分析，表明分位数回归法不但能够有效地估计模型参数，并且能够得到更好的预测效果。

基金项目

国家自然科学基金项目资助(No.61763008, 71762008)；广西自然科学基金项目资助(No.2106GXNSFAA 380194)。

参考文献

NOTES

*通讯作者