1. 引言
熟知,多元函数插值长期以来一直是计算数学研究领域的一个重要研究内容(详见文献 [1] ),当今时代是科学技术日新月异地飞速发展的时代,层出不穷的新问题要求人们提出相应的新理论,新方法来解决,对于这一类问题,目前,有关在整个空间进行插值的结果相对完备,而关于有着在六面体网格上的插值并不多见 [2] [3] 。所以本篇论文着力讲述有关六面体网格上的Lagrange插值,梁学章等人 [4] - [9] 讨论了矩形网点上的Lagrange插值方法。
六面体网格上的Lagrange插值是在矩形网点上的Lagrange插值的基础上进行的推广,其在工程设计中起着重要的作用,例如,许多机械零部件和建筑外形采用了六面体的形式,在高速,承受变载,冲击的场合中,我们会用到普通的长方体平键,而在制作平键过程中,我们可以利用插值,使它在相应场合下得到契合。
2. 基本定义和基本定理
定义1 (多元Lagrange插值问题)
设
是有界闭区域,
是k个互不相同的点,
是定义于D上的k个线性无关的s元实值连续函数(通常取为多项式).对于给定的
,欲求实线性组合
(1)
满足插值条件
(2)
这种问题称为多元Lagrange插值问题。满足条件式(2)之
称为函数
的广义插值多项式。
称为被插函数。误差函数
(3)
称为插值余项。
定义2(插值结点组)
插值条件式
中所有的点组
称为插值结点组。
定理1
若m次代数曲面
和n次代数曲面
和k次代数曲面
交点个数多于
,则一定有次数既不超过m也不超过n和k的非零多项式
存在,使得
(4)
式中,
分别为次数小于m和n和k的三元实系数多项式。
3. 具体构造方法及实验示例
设插值结点组为
(5)
令
(6)
定义
(7)
则相应得二元Lagrange插值公示为
(8)
具体算例:
1、被插值函数为
,取六面体的四个插值结点组为
,
,
,
则
,
,
,
,
,
,
,经验证
与
在插值结点组处函数值相等。
2、被插值函数为
,取六面体的十个插值结点组为
,
,
,
,
,
,
,
,
,
则
,
,
,
,
经验证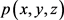 与
与 在插值结点处函数值相等。
在插值结点处函数值相等。
致谢
在论文完成之际我要特别感谢我的论文指导老师也是我硕士研究生导师崔利宏教授,还有我的小伙伴姜文芳同学。本文是在导师崔利宏教授的悉心指导和严格要求下完成的,大到各个章节,小到每个词语,导师都仔细斟酌,再三推敲,倾注了大量时间和汗水,导师质朴谦和的人生态度,正直的为人处事作风以及诲人不倦的师德深深地感染着我,他的严肃的科学态度、严谨的治学精神,精益求精的工作作风,深深的激励着我,对我的影响深远而广泛,督促我不断探索进取。在此,我向我的导师致以深深的谢意。最后,向各位尊敬的评审专家致以最诚挚的感谢,谢谢你们对本论文做出的评审以及提出的宝贵意见。
基金项目
辽宁省教育厅科研支持项目L201683661,辽宁省大学生实践基地建设项目,辽教[2015]399号。