基于改进GM模型的房价预测模型

The Housing Price Forecasting Model Based on Improved GM Model

摘要: 本文将以青岛西海岸新区商品房价格为例，针对商品房价格呈现动态变化的特点，利用改进的GM (1, 1)模型与马尔可夫模型结合，提出一种基于时间序列的预测模型，对青岛西海岸新区的商品房价格进行预测。根据灰色GM (1, 1)模型适合对数据量较少、波动不大的短期数据进行预测，而马尔可夫模型适用于数据波动较大的预测过程的特点，通过结合改进的GM (1, 1)模型与马尔可夫模型的优点，建立房价指数的预测模型。实验结果表明，该模型的拟合精度较高，是一种较为可行的房价预测模型。

Abstract: In view of the dynamic changes characteristics of real estate price, this article takes the real estate price of The West Coast New Area of Qingdao as an example, combines the improved grey GM (1, 1) forecast model with Markov model, and puts forward a new time series basing forecast model to forecast the real estate price of The West Coast New Area of Qingdao. The grey GM (1, 1) model is suitable for short-term data forecasting with fewer data and fewer fluctuations, while the Markov model is suitable for prediction processes with large data fluctuations. By combining the advantages of the improved GM (1, 1) model with the Markov model, a new forecast model is established for real estate price forecasting. The experimental results show that the accuracy of this model is high, and it is a feasible model for house price forecasting.

1. 引言

青岛西海岸新区位于山东省青岛市西岸，是由国务院于2014年6月同意批复的我国第九个国家级新区，并于27年2月入选国家重大市政工程领域PPP工作创新重点城市。与此同时，青岛西海岸新区的商品房价格也随着西海岸新区经济的飞速发展而持续飙升，房地产市场也出现供不应求的局面，引起了社会各界的广泛关注。如何有效的预判房价的走势，也成为人们心中十分关心的问题。

房价指数和影响其变化的各经济变量之间的定量关系，很难以某种常规的数学函数模型进行描述，时间序列是目前较为可行的方法之一 [1] 。商品房市场可以看作一个灰色系统来处理，GM (1, 1)预测模型是灰色系统理论的重要组成部分，是把时间序列转化成微分方程的建模过程 [2] ，主要适用于时间短、数据少、波动性不大的预测问题。马尔可夫模型是利用概率建立的一种随机型时序模型预测方法，它将时间序列看作一个随机过程，通过对事物不同状态的初始概率和各状态间的转移概率的研究，确定状态变化趋势，以预测事物的未来 [3] 。灰色预测模型与马尔可夫模型的优点可以相互补充，灰色模型用于揭示预测数据的发展趋势，马尔可夫模型用于确定状态间的转移规律。对不平稳的随机过程，可以通过部分改进方法对模型进行改进，对数据进行平滑处理，以降低波动。最终将三者结合起来，为随机波动较大的预测模型提供一种新的方法，以提高随机波动性较大的数据列的预测精度。

2. 灰色–马尔可夫模型基本原理

2.1. 灰色GM (1, 1)模型

2.1.1. GM (1, 1)模型基本形式

灰色系统建模是以灰色模块为基础，将无规律的原始数据进行累加，得到规律性较强的生成序列，建立基于最小二乘法的指数拟合曲线 [4] ，再将由生成模型得到的数据进行累减，得到原始数据的预测值。

假设原始序列数据为：

$X^{\left(0\right)}=(X^{{}^{\left(0\right)}}\left(1\right),X^{{}^{\left(0\right)}}\left(2\right),X^{{}^{\left(0\right)}}\left(3\right)\cdots X^{\left(0\right)}(n))$

一次累加生成序列为：

$X^{\left(1\right)}=(X^{\left(1\right)}\left(1\right),X^{\left(1\right)}\left(2\right),X^{{}^{\left(1\right)}}\left(3\right)\cdots X^{\left(1\right)}(n))$

其中：

$X^{\left(1\right)}\left(i\right)={\displaystyle \sum {}_{\left(k=1\right)}^i}{X}^{\left(0\right)}\left(k\right),i=1,2,3,\cdots ,n$

均值生成序列为：

$Z^{\left(1\right)}=(Z^{\left(1\right)}\left(2\right),Z^{\left(1\right)}\left(3\right)\cdots Z^{\left(1\right)}(n))$

其中：

$Z^{\left(1\right)}\left(k\right)=\frac{X^{\left(1\right)}\left(k\right)+X^{\left(1\right)}\left(k-1\right)}{2},k=2,3,\cdots ,n$

则将：

$X^{\left(0\right)}\left(k\right)+\alpha \cdot Z^{\left(1\right)}\left(k\right)=b$

称为GM (1, 1)模型的基本形式 [5] 。

2.1.2. GM (1, 1)模型作用机理

由于 $X^{\left(1\right)}$ 是基于时间t的序列，具有基于时间序列的变化规律，因此对 $X^{\left(1\right)}$ 建立关于时间t的一阶线性微分方程，得到：

$\frac{\text{d}{x}^{\left(1\right)}\left(k\right)}{\text{d}t}+\alpha x^{\left(1\right)}\left(k\right)=\mu$ (1)

其中：α称为发展灰度，反映了累加生成序列 $X^{\left(1\right)}$ 的发展趋势；μ称为内生控制灰度，反映了数据间的变化关系。

由于灰色模型适用于离散型数据，所以我们利用均值生成序列 $Z^{\left(1\right)}$ 代替累加生成序列 $X^{\left(1\right)}$ ，得到：

$\frac{\text{d}{x}^{\left(1\right)}\left(k\right)}{\text{d}t}+\alpha z^{\left(1\right)}\left(k\right)=\text{μ}$

又因为：

$\frac{\text{d}{x}^{\left(1\right)}\left(k\right)}{\text{d}t}=\frac{X^{\left(1\right)}\left(k\right)-X^{\left(1\right)}\left(k-1\right)}{1},k=2,3,\cdots ,n$

所以将式(1)离散化后得：

$X^{\left(1\right)}\left(k\right)-X^{\left(1\right)}\left(k-1\right)+\alpha z^{\left(1\right)}\left(k\right)=\text{μ},k=2,3,\cdots ,n$ (2)

利用最小二乘法求解式(2)，得到：

$\left[\begin{array}{c}\alpha \\ \text{μ}\end{array}\right]={\left(B^{T}B\right)}^{-1}{B}^{T}Y$

其中：

$B=\left[\begin{array}{cc}-z^{\left(1\right)}\left(2\right)& 1\\ \begin{array}{c}-z^{\left(1\right)}\left(3\right)\\ ⋮\\ -z^{\left(1\right)}\left(n\right)\end{array}& \begin{array}{c}1\\ ⋮\\ 1\end{array}\end{array}\right]Y=\left[\begin{array}{c}{x}^{\left(0\right)}\left(2\right)\\ \begin{array}{c}{x}^{\left(0\right)}\left(3\right)\\ ⋮\end{array}\\ x^{\left(0\right)}\left(n\right)\end{array}\right]$

求得α和μ后，继续求解微分方程(1)得：

${\hat{X}}^{\left(1\right)}\text{=}c{e}^{-\alpha t}+\frac{\text{μ}}{\alpha }$ (3)

其中： ${\hat{X}}^{\left(1\right)}$ ⁾是 $X^{\left(1\right)}$ 序列的预测值序列，c为待定系数

将式(3)离散化，得到：

${\hat{X}}^{\left(1\right)}\left(k+1\right)=c{e}^{-\alpha k}+\frac{\text{μ}}{\alpha },k=0,1,2,3,\cdots n-1$ (4)

为求待定系数c的值，假设 ${\hat{X}}^{\left(1\right)}\left(1\right)=X^{\left(1\right)}\left(1\right)=X^{\left(0\right)}\left(1\right)$ ，则有：

${\hat{X}}^{\left(1\right)}\left(1\right)=c+\frac{\text{μ}}{\alpha }=X^{\left(0\right)}(1)$

可得： $c=X^{\left(0\right)}\left(1\right)-\frac{\text{μ}}{\alpha }$ 。

将c带入式(4)得：

${\hat{X}}^{\left(1\right)}\left(k+1\right)=\left(X^{\left(0\right)}\left(1\right)-\frac{\text{μ}}{\alpha }\right)e^{-\alpha k}+\frac{\text{μ}}{\alpha }k=0,1,2,3，\cdots ，n-1$ (5)

式(5)表示基于微分方程生成的离散的累加预测值序列。

对式(5)做累减还原，即可得到原始序列 $X^{\left(0\right)}$ ⁾的灰色预测值序列：

${\hat{X}}^{\left(0\right)}\left(k+1\right)={\hat{X}}^{\left(1\right)}\left(k+1\right)-{\hat{X}}^{\left(1\right)}\left(k\right),k=1,2,3,\cdots ,n-1$ (6)

将式(5)带入式(6)得：

${\hat{X}}^{\left(0\right)}\left(k+1\right)=\left(X^{\left(0\right)}\left(1\right)-\frac{\text{μ}}{\alpha }\right)e^{-\alpha k}\cdot \left(1-e^{\alpha }\right)$ (7)

式(7)即为灰色GM (1, 1)预测模型得到的最终预测值序列。

2.2. 马尔可夫模型

马尔可夫模型表示数学中具有马尔可夫性质的随机的基于时序的建模过程，所谓马尔可夫性质是指对于随机过程 $\left\{x_n,nT\right\}$ (T表示时刻的集合)和离散状态集 $I=\left\{i_1,i_2\cdots \right\}$ ，对于任意n T，其条件概率满足：

$P\left\{x_{n+1}=i_{n+1}|x_0=i_0,x_1=i_1,\cdots x_n=i_n\right\}=P\left\{x_{n+1}=i_{n+1}|x_n=i_n\right\}$

即某一时刻t系统处于状态i的概率，只与其前一个时刻的状态有关，与过去的状态无关，该性质称为马尔可夫属性。

2.2.1. 状态区域划分

马尔可夫模型状态区域划分：构造以中心上下对称的等宽条形带为拟合曲线 $\hat{Y}\left(k\right)$ ，时间变化不影响各条形带宽度，每个条形区域代表一个状态 [6] ，其任一状态区间Q_i表示为 $Q_i=\left[Q_{1i},Q_{2i}\right]$ 。

其中： $Q_{1i}=\hat{Y}\left(k\right)+A_i、Q_{2i}=\hat{Y}\left(k\right)+B_i且A_i=a_i\bar{y},B_i=b_i\bar{y}$ ， $\bar{y}$ 表示原始数据的均值，a_i、b_i为常数。一般地，状态取灰色模型拟合曲线为中心的上下对称等宽条形带 [1] 。

2.2.2. 状态转移概率矩阵

将数据序列划分为若干状态，记为 $\left\{E_1,E_2,\cdots E_n\right\}$ ，每个条形区域代表一个状态。

记：数据序列在时刻m的状态为E_i，经过m + k时刻状态转移到E_j的概率为 $P_{ij}^{\left(k\right)}$ ，且满足：

$P_{ij}^{\left(k\right)}=\frac{m_{ij}^{\left(k\right)}}{M_i}$

$m_{ij}^{\left(k\right)}$ 表示状态E_i经过k步转移到状态E_j的次数，M_i为状态E_i出现的总次数。

以状态转移概率 $P_{ij}^{\left(k\right)}$ 为元素的矩阵，称为马尔可夫模型的k步状态转移概率矩阵，其满足每行 $P^{\left(k\right)}$ 之和为1 [7] 。

$P^{\left(k\right)}\text{=}\left|\begin{array}{cc}\begin{array}{cc}{P}_{11}^{\left(k\right)}& P_{12}^{\left(k\right)}\\ P_{21}^{\left(k\right)}& P_{22}^{\left(k\right)}\end{array}& \begin{array}{cc}\cdots & P_{1n}^{\left(k\right)}\\ \cdots & P_{2n}^{\left(k\right)}\end{array}\\ \begin{array}{cc}⋮& ⋮\\ P_{n1}^{\left(k\right)}& P_{n2}^{\left(k\right)}\end{array}& \begin{array}{cc}\dots & ⋮\\ \dots & P_{nn}^{\left(k\right)}\end{array}\end{array}\right|$

2.2.3. 计算预测值

若当前系统处于状态Ei，此时Pij描述了状态Ei经过一步转向状态Ej的可能性 $\left(j=1,2,\cdots n\right)$ 。按照最大概率原则，选择 $\left\{P_{i1},P_{i2},\cdots Pin\right\}$ 中最大者对应的状态，即当 $P_{ij}=\max \left\{P_{i1},P_{i2},\cdots Pin\right\}$ 时，可以预测系统下一步转向状态Ej。当系统状态确定了以后，也就确定了预测值的状态区间 $Q_i=\left[Q_{1i},Q_{2i}\right]$ ，则其预测值可以用该区间的中位数来表示 [8] 。

3. 改进的灰色模型

谢乃明等 [4] 已经证明，GM (1, 1)模型的预测误差主要是由于将式(1)离散化得到式(2)过程造成的。为了改善GM (1, 1)模型的性能，降低模型的拟合误差，由此衍生出很多改进方法。田红霞 [9] 利用二次多项式拟合的方法，可以提高GM (1, 1)模型的预测精度；李瑶等 [10] 使用模糊集理论建立动态GM (1, 1)模型提高了模型的预测精度；刘呈玲等 [11] 利用弱化算子处理法也可以提高GM (1, 1)模型的预测精度。本文将基于多项式拟合法，分别利用多种不同多项式，对模型进行拟合，并最终比较选择最优方法，应用于本次实验。

改进过程:

先利用GM (1, 1)算法建立原始灰色预测模型,得到系统预测值序列，然后分别用不同拟合方法对生成的预测数据与原始实际值进行拟合修正，减小由数据离散化过程带来的系统误差，并以皮尔逊相关系数作为衡量模型拟合效果好坏的评定标准,最终选用拟合效果最佳的方法改进GM (1, 1)模型，建立改进的GM (1, 1)模型。

经实验验证，不同拟合方法拟合效果对比如下：

1) 传统GM (1, 1)算法：

预测模型为：

$X^{\left(0\right)}\left(t+1\right)=\left(1-e^{-0.02092}\right)\cdot \left(10.437-\frac{11.4556}{-0.02092}\right)e^{0.02092t}$

相关系数 $corrcoef=0.94968753$

2) 利用二次多项式拟合改进：

拟合模型为：

$Y\left(x\right)=0.12538X^2+11.428837X-0.707217$

相关系数 $corrcoef=0.92035854$

3) 利用三次多项式拟合改进：

拟合模型为：

$Y\left(x\right)=0.010056X^3-0.115960X^2+13.023698X-3.16889$

相关系数 $corrcoef=0.9447651$

4) 利用四次多项式拟合改进：

拟合模型为：

$Y\left(x\right)=-0.000504X^4+0.0182631X^3-0.2263819X^2+1.383664X+9.4540461$

相关系数 $corrcoef=0.95699527$

5) 利用指数多项式拟合改进：

拟合模型为：

$Y(x)=14.5871851128\cdot e^{-\frac{{}^{0.420828817852}}{x}}$

相关系数 $corrcoef=0.79140786$

6) 利用对数多项式拟合改进：

拟合模型为：

$Y\left(x\right)=1.7297367+\log \left(x\right)+10.13768756$

相关系数 $corrcoef=0.88990066$

由于随着n次多项式次数的增高，高次项的系数会变得非常小，即模型的拟合程度与高次项的相关性很低，因此本实验不再进行更高次数的多项式拟合。

上述实验数据表明，四次多项式拟合模型的皮尔逊相关系数最接近于1，表明该模型拟合程度最高，因此我们利用该四次多项式对GM (1, 1)算法进行改进，然后在利用改进后的GM (1, 1)算法进行后续工作。

4. 应用实例

4.1. 建立改进的GM (1, 1)模型

本文选取安居客网址提供的2017年3月至2018年5月青岛市西海岸新区月平均房价为原始数据，并以此除以1000得到实验所需初始数据：

Table 1. Comparison of GM (1, 1) model and modified GM (1, 1) model

表1. GM (1, 1)模型与改进的GM (1, 1)模型数据对比

X⁽⁰⁾ = (10.437, 11.670, 12.311, 12.855, 13.067, 13.192, 12.824, 12.693, 12.885, 13.357, 13.856, 14.420, 14.981, 15.590, 16.049 )

利用改进的GM (1, 1)算法建立预测模型，并用于本次实验(实验数据如表1所示)。

GM (1, 1)模型与改进的GM (1, 1)模型，对原始实际数据的拟合效果如图1所示：

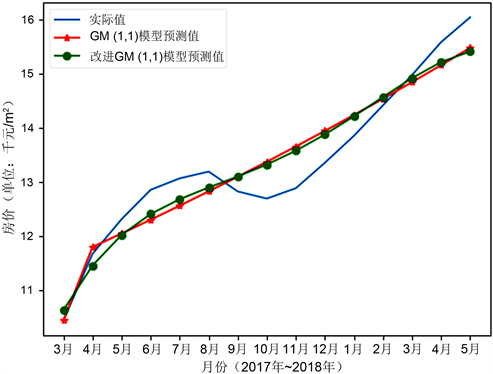
Figure 1. Comparison of the fitting effect between GM (1, 1) model and modified GM (1, 1) model

图1. GM (1, 1)模型与改进的GM (1, 1)模型拟合效果对比

并以此模型得到的2018年6月份得数据预测值为15.439，还原得到青岛市西海岸新区2018年6月份的月平均房价预测值为：

4.2. 利用马尔可夫模型修正

4.2.1. 状态区间划分

根据改进的GM (1, 1)模型输出的预测值与实际数据的偏差，进行状态划分。基于表1可以看出，实验所得的相对误差范围为：−5.39%~3.95%，我们对此范围进行状态区间划分。状态区间的划分并无严格要求，但当数据量较小时，状态区间划分数量较小为宜。本实验中，我们依据上述实验误差范围，将状态均匀划分为4个区间，划分结果如表2所示。

4.2.2. 构建状态转移概率矩阵

根据状态区间分布，建立改进的灰色–马尔可夫模型状态转移概率分布矩阵：

$P^{\left(1\right)}=\left[\begin{array}{cc}\begin{array}{cc}\frac{2}{3}& \frac{1}{3}\\ \frac{1}{4}& \frac{1}{4}\end{array}& \begin{array}{cc}0& 0\\ \frac{1}{4}& \frac{1}{4}\end{array}\\ \begin{array}{cc}0& 0\\ 0& \frac{1}{6}\end{array}& \begin{array}{cc}0& 1\\ 0& \frac{5}{6}\end{array}\end{array}\right]P^{\left(2\right)}=\left[\begin{array}{cc}\begin{array}{cc}\frac{1}{3}& \frac{2}{3}\\ \frac{1}{4}& 0\end{array}& \begin{array}{cc}0& 0\\ \frac{1}{4}& \frac{2}{4}\end{array}\\ \begin{array}{cc}0& 0\\ \frac{1}{5}& \frac{1}{5}\end{array}& \begin{array}{cc}0& 1\\ 0& \frac{3}{5}\end{array}\end{array}\right]P^{\left(3\right)}=\left[\begin{array}{cc}\begin{array}{cc}0& \frac{2}{3}\\ 0& 0\end{array}& \begin{array}{cc}\frac{1}{3}& 0\\ 0& 1\end{array}\\ \begin{array}{cc}0& 0\\ \frac{2}{5}& \frac{1}{5}\end{array}& \begin{array}{cc}0& 1\\ 0& \frac{2}{5}\end{array}\end{array}\right]$

一步转移概率矩阵 二步转移概率矩阵 三步转移概率矩阵

Table 2. Results of state interval division

表2. 状态区间划分

由于2018年5月份数据系统状态处于4状态，并且经过比较，状态4的1、2、3步状态转移概率如表3所示：

Table 3. Results of state transition probability

表3. 状态转移概率

所以当系统状态处于区间4时，下一步最有可能的转移情况是转移到状态4，我们用状态区间4误差范围的中位数代表该区间的平均误差，区间4的误差范围是(1.61%~3.95%)，中位数为2.78%，所以我们用此中位数作为马尔可夫模型对改进的GM (1, 1)的修正系数，修正之后的数值为

$\frac{15.439}{1-2.78\%}=15.880$

经过还原得到最终由改进的灰色–马尔可夫模型预测的2018年6月青岛市西海岸新区商品房的月平均房价为15.880*1000 = 15880元/m²。

5. 结束语

本文以传统灰色GM (1, 1)预测模型为出发点，对青岛市西海岸新区商品房价格的预测问题进行了初步分析，然后利用多项式拟合的方法，对由传统灰色GM (1, 1)模型得到的数据进行平滑性修正，最后再结合马尔可夫链的特点，利用状态转移概率矩阵，对改进的GM (1, 1)预测模型得到的预测数据进行稳定性修正，由此降低了系统生成数据的随机性。改进后的灰色–马尔可夫模型既考虑了基于时间序列的数据特点的挖掘，同时又通过后期修正，平滑了原始数据的随机波动性特征，最终得到一个精度较高，适用性较强的基于时间序列预测模型。