1. 引言
材料力学课程是材料类专业、机械类专业及土木类等专业的一门重要的基础课,材料力学性质的微观机理及表征一般采用多媒体方法向学生展示,学生无法进行实验验证及深层分析,大大限制了学生的学习积极性、求知欲。TiO2是一基本的化工原料,其结构在固体物理类课程中为典型晶体结构,TiO2纳米管以其独特的物理、化学及结构性质已经被广泛地应用于多相催化反应、气敏传感性 [1] 、染料敏华电池 [2] 、生物材料 [3] 及储氢材料 [4] 等多个领域。目前,二氧化钛纳米管的制备方法主要有水热合成法 [5] 及电化学阳极氧化法 [6] ,两种方法制备纳米管的机理不同。纳米TiO2主要有两种结晶形态:一种是锐钛型,另一种是金红石型,随着温度的升高,TiO2主要以金红石型为主 [7] ,并且金红石型的TiO2更加稳定和致密,所以其拉伸性能等物理化学性质都相对突出 [8] 。
LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator) [9] 是由美国国家能源部下的Sandia国家实验室开发的基于牛顿力学的经典分子动力学模拟的开源软件,可以模拟液体、固体或气态的粒子集合,它可以使用各种力场和边界条件来模拟原子、聚合物、生物、金属、颗粒和粗粒度系统,更适合金属及金属氧化物力学性质预测。本文主要模拟TiO2纳米管分别在100 K、500 K、1000 K、1500 K、2000 K和2500 K的不同温度下拉伸的力学性质,在NPT系综下采用z轴方向单轴拉伸方法。
2. 建立模型
通过LAMMPS内建模型处理命令建立一个圆筒模型,将锐钛矿相TiO2块体材料除去外径3.0 nm以外的原子及内径2.0 nm以内的所有原子形成圆筒外径为3.0 nm,内径为2.0 nm,管壁厚度为0.5 nm的TiO2纳米管,如图1所示。该模型的纳米管共有48,000个原子,其中16,000为钛原子,按化学计量比的氧原子数为32,000个。通过Ovito软件对模拟结果进行三维可视化及数据分析,对其建立共价键连接氧原子和钛原子,改变原子的半径大小,最后得出的TiO2纳米管的效果如图1。其中蓝色表示氧原子,红色表示钛原子。建模过程应用了大量晶体学知识,将所学的晶体学与材料力学有机的联系在一起,有利于促使学生所学专业知识的融会贯通。
结合理论物理及固体学知识可以,分子动力学计算需要选择必要的势函数来对模型进行描述,计算采用势函数的Buckingham势函数 [10] ,此函数的表达式为:
(1)
其中ρ是离子对依赖长度参数,而rc是截断距离,当原子间的距离超过rc时,认为原子间的相互作用为0。势函数中的ρ必须大于零,系数A、ρ和C可以被写成ε和σ的解析表达式,可类比于Lennard-Jones势函数 [11] 的表达。式中A表示能量单位,ρ表示距离单位,C表示能量距离单位的6次方。
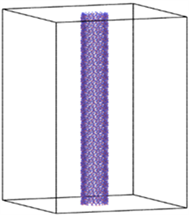
Figure 1. TiO2 nanotube model built by Lammps command
图1. 采用Lammps内建命令所建立的TiO2纳米管模型
3. 实验过程
3.1. 温度与抗拉强度的关系
众所周知,材料的力学性质受温度影响很大,利用传统的万能材料测试机进行实验不能研究材料的温度影响,目前市售的材料力学仿真软件一般采用植入数据方法也不能研究温度对材料性能的影响,而本文采用分子动力学方法研究材料的拉伸性质可实现在精确的环境温度下进行模拟计算,所获得结果真实可靠。如图2和图3中所示,当模拟温度在100 K时,随材料应变量的增大,材料表现出的应力迅整上升,达到峰值后快速下降,该应力应变规律与利用万能材料实验机所获数据十分相似,该曲线可替代真实验材料拉伸实验中应力曲线的获得及分析;此外通过分析不同温度对TiO2纳米管抗拉强度影响可知:温度从100 K升高到500 K,抗拉强度减小;随着温度从500 K上升到2500 K,TiO2纳米管的抗拉强度又逐渐增大。实验结果显示,温度为100 K时材料的应力为0.456 GPa略大于2500 K时的0.453 GPa。
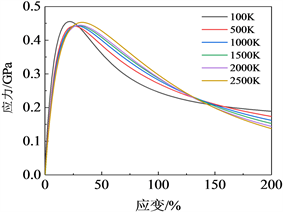
Figure 2. Tensile stress-strain diagrams of TiO2 nanotubes at different temperatures
图2. 不同温度下TiO2纳米管拉伸应力-应变图

Figure 3. Relationship between tensile strength and temperature
图3. 抗拉强度与温度关系图
3.2. 拉伸形态以及受力分析
将分子动力学应用于教学过程的另一魅力在于可以通过三维可视化软件观察材料拉伸过程中每个原子的变化及受力,给合晶体学知识及力学知识找出拉伸实验应力变化的根源。本实验通过Ovito开源软件进行模拟过程可视化,如图4所示。以2500 K时TiO2纳米管的拉伸过程的变化为例进行演示,观察到拉伸应变小于0.5时,TiO2纳米管变形量较小,原子之间的成键相对稳定,但由于键长伸长,表现为原子之间的吸引力,宏观表现为应力迅速增加;当拉伸应变超过0.5时,部分原子之间的键出现断裂,宏观表现为应力快速下降;由于部分化学键断裂使原子向管内发生位移表现为宏观的颈缩现象。

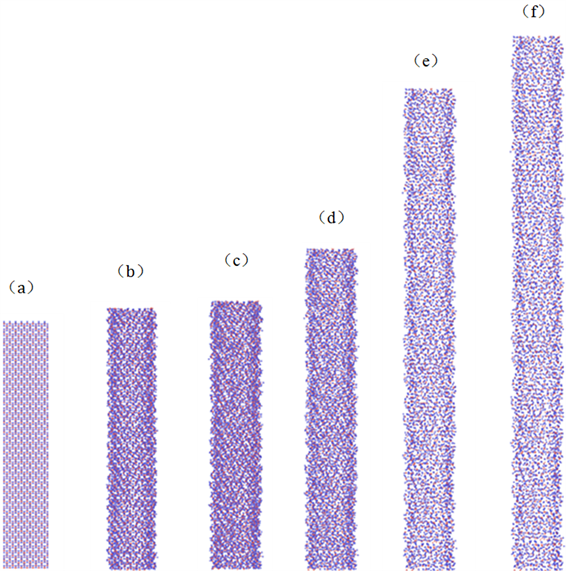
Figure 4. The strains of titanium dioxide nanotubes during tensile deformation at 2500 K are: (a) 0; (b) 0.5; (c) 1.0; (d) 1.2; (e) 1.5; (f) 2.0, respectively
图4. 2500 K下二氧化钛纳米管拉伸变形过程中应变分别为:(a) 0; (b) 0.5; (c) 1.0; (d) 1.2; (e) 1.5; (f) 2.0
为定量表达拉伸过程中原子之间的距离变化,引入径向分布函数 [12] (radial distribution function, RDF)又称“对相关函数”(pair correlation function),其主要表征流体和非晶态固体结构,用于表示与某个粒子距离为r到r + △r之间的粒子的平均数,定义为:
(2)
式中:Ni、Nj分别为i原子在系统中的总数;V为总体积;
表示以i类粒子为中心,从r到
之间壳层类的j原子总数。
由径向分布函数径定义可知,该函数为热力学统计物理课程的概念,通过大量原子的行为进行系综平均,该函数实际上表征了系统内粒子的分布情况,或局部结构与总体结构的差异。如果系统粒子的分布是完全随机的,不存在任何距离内的有序性,则径向分布函数应处处为1,而真实体系的径向分布函数往往在一个较短距离内有若干起伏的峰值,随距离的增大最后稳定到1,这正是非理想流体与非晶固体的短程有序、长程无序的结构特征。
2500 K下TiO2纳米管在截断半径为1 nm的径向分布函数随应变的变化如图5所示,结果表明TiO2纳米管被逐渐拉伸的过程,相邻原子之间距离约0.19 nm,也就说明了钛原子和氧原子之间的距离在0.19 nm左右,与文献 [13] 所得的结果相符合。从图中也可以看出随着应变的逐渐增大,第一峰峰位也逐渐向右移动,即钛原子和氧原子的距离增大。通过观察局部放大径向分布函数图可以看出拉伸前50% TiO2纳米管没有较大的变形,结构较为稳定,当拉伸超过50%后,TiO2纳米管开始逐渐变形,结构稳定性下降。这也印证了图4中TiO2不同拉伸应变的结果,当应变超过了1.0后,纳米管稳定性逐渐降低。
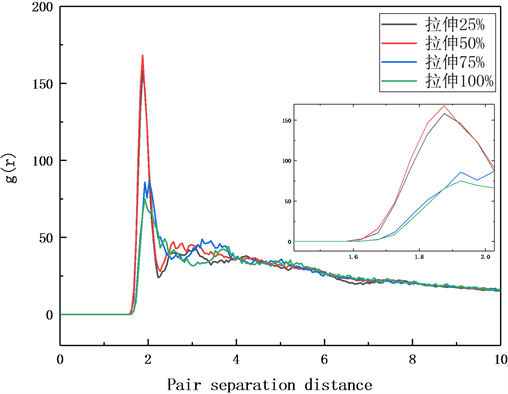
Figure 5. Radial distribution function diagram and partial enlargement diagram of 2500 K TiO2 nanotubes under different tensile states
图5. 2500 K TiO2纳米管不同拉伸状态下径向分布函数图及其局部放大图
利用Ovito软件将2500 K下TiO2纳米管每个原子的受力进行显示,TiO2纳米管在未受应力时,每个原子受力很小,且指向化学键的方向,该力主要是克服由于温度造成的原子在平衡位移的振动;当TiO2纳米管发生应变时,每个原子的所受力的方向和大小开始发生剧烈变化,随着TiO2纳米管逐渐被拉伸,每个原子所受到的力都变得没有规律,每个原子受到力的方向也不断变化,正是由于这些看似杂乱的力使材料产生了宏观应力及颈缩效应;当应变达到某一临界值时,材料内部大量化学键断裂,如图6(d)~图6(f)所示,部分原子处于不受力的自由状态,使材料表现为宏观应力下降。
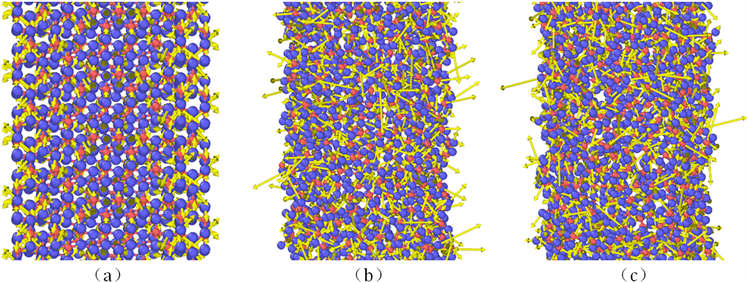

Figure 6. Atomic force analysis of TiO2 nanotubes under different tensile strains at 2500 K; (a) strain 0; (b) strain 0.5; (c) strain 1; (d) strain 1.2; (e) strain 1.5; (f) strain 2
图6. 2500 K下TiO2纳米管不同拉伸应变下原子受力分析;(a) 应变0;(b) 应变0.5;(c) 应变1.0;(d) 应变1.2;(e) 应变1.5;(f) 应变2.0
4. 总结
通过本教学项目的实施,学生可以通过构建出48,000个原子组成的TiO2纳米管,熟悉和应用晶体学知识;通过对不同温度下拉伸曲线的分析使学生认识材料在不同温度下的力学性质变化规律;通过对不同应变下材料的微观结构受力分析,可以使学生对固体物理、晶体学知识与材料力学知识系统的认识,并能获得由理论向实践、由微观向宏观的思想升华;通过对关联函数的分析,可以将热力学统计概念引入到材料力学实验,有利于扩大学生视野,提高学生的学习思维。总之,通过分子动力学方法来仿真材料力学基本实验可以有效提高学生的科学素养,提高学生科学素质。
基金项目
海南大学教育教学改革项目(项目编号:hdjy1911);海南大学材料与化工学院教育教学改革项目(项目编号:Chjy1802)。