1. 引言
搅拌摩擦焊(Friction Stir Welding, FSW)是英国焊接研究所发明的一种新型固相连接技术,在航空航天、船舶和海洋工程、轨道交通等领域有着广泛的应用 [1] [2] [3] 。在FSW过程中,材料的塑性流变直接决定焊缝的宏观组织分区(焊核区、热机影响区、热影响区),影响宏观焊接缺陷(孔洞、底部未焊透和隧道等)和特征微观结构(包括FSW接头特有的洋葱环、“S”线、弱连接、分层、偏析带和织构等)的状态和分布,对焊接接头的性能具有重要的影响。不管是搅拌头的形状,还是焊接速度、旋转转速等焊接参数,都直接影响焊接过程中金属的塑性流动。同时,被焊材料的不同也导致了焊接过程中材料流动的差异。因此焊接过程的材料塑性流变是FSW的一个研究重点,也是研究FSW接头组织和性能的基础。然而焊接过程中材料的流动过程是不可见的,深入理解FSW过程中材料的流动行为受到限制。目前对该方面的研究还处于探索阶段,尚无完整的关于FSW过程材料塑性流变的理论体系。
随着计算机技术的发展以及数值分析能力的提高,基于有限元方法的数值模拟技术以其低成本、高效率的优点及可视化和过程再现能力已成为研究FSW过程的一种重要手段,并对建立和完善其理论基础、指导焊接工艺参数的制定具有重要的意义。基于计算流体动力学(Computational Fluid Dynamics, CFD)理论建立的FSW数值模型广泛应用于FSW中的材料流动模拟研究。基于CFD 理论的模型,将被焊材料看作非牛顿流体,通过有限体积法求解流体力学基本方程。CFD模型采用传统的欧拉网格技术,不考虑搅拌头和工件的接触,可以有效避免网格畸变,其计算成本较低。本文基于CFD理论,建立FSW过程热流耦合模型,通过计算获得焊后工件材料流动情况,为实际生产提供指导。
2. CFD模型的建立
2.1. 控制方程
CFD数学模型将被焊材料假设为流体,流体是一种因受到剪切力作用而发生连续变形的物质,它具有连续性、易流动性、粘性和压缩性等物理性质,同时其流动时也满足质量守恒定律、动量守恒定律和能量守恒定律。CFD数学模型以这三个基本定律为基础,并以积分或者微分形式的方程组进行描述,把这些方程中的积分或者微分用离散的代数式来进行代替,把这些基本方程化为代数方程组;然后,通过用计算机来对这些代数方程组进行求解运算,就可以得出流动场在离散时间或者空间上的数值解 [4] [5] [6] 。
流体的连续性是基于连续介质模型提出的,是一种充满整个空间且无间隙的连续体,这种连续性主要表现在密度、位移速度和变形速度等表征流体性质的物理量的连续分布上。由质量守恒原理可知,微元体内质量的增加率等于单位时间内流入微元面的净流入质量。因此,流体连续性的数学描述(即连续性方为 [7] [8] [9] :
(1)
其中
是速度分量,i为1、2和3分别表示x,y,z方向的速度分量。那么单相稳态下方程为:
(2)
其中
为密度,
为粘度,P为压力,有效塑性应变率表达为:
(3)
为应变率张量,其定义为:
(4)
那么,温度可由如下能量守恒方程计算:
(5)
其中
为比热,T为温度,k为热导率。
2.2. 材料模型
FSW稳态焊接过程中,焊缝金属的材料流动不仅受到焊接温度场的影响,还受到搅拌头形貌、焊接工艺和其与搅拌头接触状态等众多因素的影响。为建立能有效描述其流动行为的数学模型,必须对其进行抽象处理。并做简化与假设:假设焊缝材料为非牛顿流体。稳态焊接过程中,焊件温度并非恒定温度,而是呈一定规律分布。根据牛顿内摩擦定律可知,其流动速度梯度与剪应力大小不成正比,故其属于非牛顿流体;假设焊件流动材料为不可压缩流体。焊接过程中,焊缝材料流动的最大速度远小于搅拌头旋转线速度,表现为低速流动且材料本身不易被压缩,因此可将其视为不压缩流体。
搅拌摩擦焊接成形过程中,金属材料在理想塑性条件下发生高温状态下的大变形材料流动。此时,将焊缝金属材料视为与速度和温度有关的高粘度流体,并通过输入与流动应力
有关的粘度函数
来描述其耦合属性,其中流动应力
是一个与变形速度和温度有关的量;同时将金属材料与搅拌头间的摩擦生热和金属材料内部的流动变形产热视为热源,则可以将焊接过程视为热传导方程与不可压缩Navier-Stokes方程相互耦合的非线性问题。
粘性作为流体的固有属性,是指流体在流动过程中具有抵抗剪切变形的特性,粘性的大小用与温度有关的粘度来度量。等效应力表达式为:
(6)
由式(3),切应力和粘度、应变率之间的关系为:
(7)
所以等效应力和等效塑性应变率以及粘度之间的关系可以表示为以下的公式:
(8)
根据
(9)
所以
(10)
其中流动应力
是一个与变形速度和温度有关的量;同时将金属材料与搅拌头间的摩擦生热和金属材料内部的流动变形产热视为热源,则可以将焊接过程视为热传导方程与不可压缩Navier-Stokes方程相互耦合的非线性问题。本文被焊材料采用6061铝合金,其热物理性能随温度变化如表1 [9] 所示。

Table 1. Material properties of 6061Al alloy used in model
表1. 6061铝合金材料性能参数
2.3. 几何模型
设定工件几何尺寸为120 mm × 30 mm × 3 mm。搅拌头作为刚体处理,在建立计算域时,将搅拌头表面作边界处理,并对计算域进行六面体网格剖分。FSW过程中搅拌头与被焊工件发生相对位置变化。搅拌头的移动会导致计算域的形状发生改变,为简化计算过程,本文采用入口–出口的方式对模拟中的物理过程进行简化,即材料从板材入口以焊接速度流入计算域,从对侧出口流出计算域。
3. 结果与分析
3.1. 速度场
设定焊接速度为120 mm/min,搅拌头旋转速度分别为600 r/min、900 r/min和1200 r/min,图1所示为不同旋转速度下搅拌头周围前进侧(AS)及后退侧(RS)材料速度矢量图,从图中可以看出,材料在在搅拌头附近循环流动。搅拌头轴肩附近材料的流动速度远高于搅拌头附近材料,最大速度出现在轴肩周围。这是因为搅拌头轴肩外缘处有最大速度。并且由于轴肩的旋转摩擦及压力的作用,轴肩附近材料有向下绕流的趋势;搅拌头底部及附近的大部分材料随着搅拌头的旋转有向上绕流的趋势,在远离搅拌头的区域,流动速度较小,流动性变低。随着旋转速度增加时,轴肩处的最大流体速度从0.285 m/s增加到0.558 m/s,搅拌头附近区域材料流动性明显增强,这主要是由于当搅拌头高速旋转时,产生了更多的热量,被焊材料粘度减小导致。因此,在焊接速度保持不变的情况下,可通过提高搅拌头旋转速度增加被焊区域材料的塑性流动速度。
设定搅拌头旋转速度为900 r/min,焊接速度分别为60 mm/min、120 mm/min和180 mm/min,图2所示为搅拌头周围材料速度矢量图,从图中可以看出,焊接速度改变时,搅拌头附近区域的材料流动行为基本相同,不同焊接速度下,搅拌头轴肩边缘流体速度最大值分别为0.423 m/s、0.422 m/s、0.422 m/s,可以看出焊接速度对材料的流速变化影响不明显。
 (a)
(a)  (b)
(b) 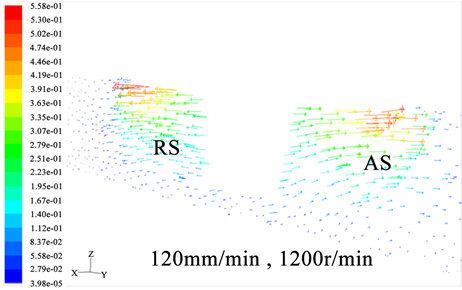 (c)
(c)
Figure 1. Vector diagram at different rotation velocities
图1. 不同旋转速度下的速度矢量图
 (a)
(a)  (b)
(b)  (c)
(c)
Figure 2. Vector diagram at different welding velocities
图2. 不同焊接速度下的速度矢量图
3.2. 材料流动轨迹及应变率
图3所示给出了搅拌头周围材料的流线图。模拟得到的流线图与铜箔标记法实验所得特征符合 [10] ,从图中可以得到,在搅拌头周围的材料的流动方向和搅拌头旋转方向相同。无论是AS和还是RS,材料都是随着搅拌头旋转方向流动,搅拌头前方的材料平行于焊接方向流动。并在RS的相应位置释放。材料流入搅拌头轴肩范围后,在摩擦力作用下,材料在搅拌头前方区域发生分流,在搅拌头后方区域形成焊合,距离搅拌头较远的材料由于受搅拌头作用较小,仍然按原来的方向流动。焊缝表面位置部分塑性金属主要受轴肩摩擦和挤压作用,塑性金属流动充分,变形区宽度比轴肩直径略大,距离搅拌头越近材料的流动越剧烈。从流线模拟结果可以看出,材料发生分流与焊合都出现在AS位置。模拟结果能够在一定程度上解释FSW过程中的缺陷倾向于在前进侧出现的普遍现象。

Figure 3. Material streamline around pin
图3. 搅拌头周围材料流线图
图4为搅拌头转速恒定900 r/min时,不同的焊接速度(60 mm/min、120 mm/min和180 mm/min)对应变速率的影响。从图中可以看出,最大应变速率出现在与轴肩接触的焊件表面位置,分别为1783.2 l/s、1781.7 l/s和1781.6 l/s,以应变速率表征材料的流动剧烈程度,可以得出增加焊接速度不能提高焊件表面的流动性。焊件底面的应变速率分别为0.2032 l/s、0.4050 l/s和0.6040 l/s,可以得出增加焊接速度可以增强焊件底部的流动性。因此增加焊接速度不能提高焊件表面的流动性,但是可以增强焊件底部的流动性。
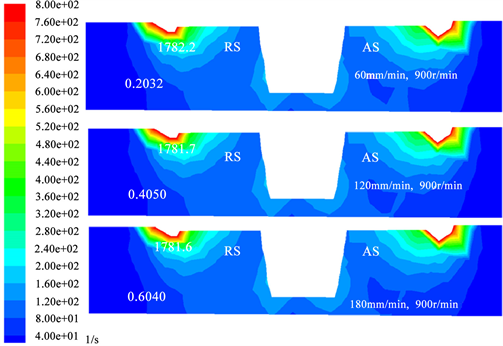
Figure 4. Strain rate nephogram at different welding velocities
图4. 不同焊接速度下的应变速率云图
图5为焊接速度恒定120 mm/min时,不同的搅拌头转速(600 r/min、900 r/min和1200 r/min)对应变速率的影响,从图中可以看出,随着搅拌头的转速增加,焊件表面的应变速率分别为1191.1 l/s、1781.7 l/s和2370.1 l/s,可以得出增加搅拌头的转速可以明显提高焊件表面的流动性。焊件底面的应变速率分别为0.3977 l/s、0.4050 l/s和0.4056 l/s,可以看出,增加焊接速度,焊件底部的流动性变化不明显。因此,可通过增加搅拌头转速提高焊件表面的流动性,但是转速的提高对焊件底部的流动性没有影响。并且可以看出焊件焊接区域内,从焊件底部到焊件表面,焊件的应变速率越来越大,因此可以得出焊接区域内,从焊件底部到焊件表面,材料的流动性逐渐增加。
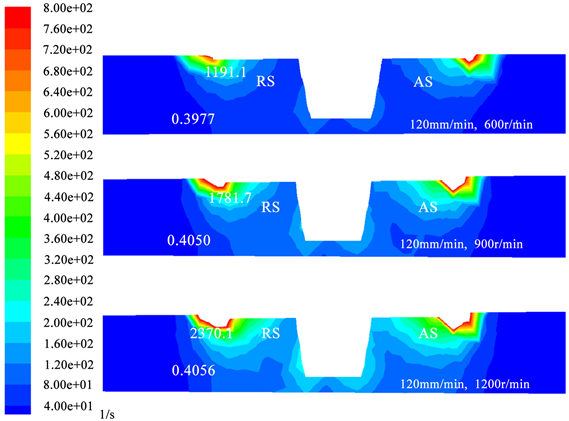
Figure 5. Strain rate nephogram at different rotational velocities
图5. 不同旋转速度下的应变速率云图
综上所述,搅拌头周围材料呈现分层流动的现象,与轴肩接触的焊件表层材料流速最大,搅拌头根部附件的底层材料流速较小,底部位置材料流动不充分是形成缺陷的主要原因;这种现象的主要原因是与轴肩接触的材料由于摩擦力的作用产热量最大,该处材料粘性小,流动性好。而远离搅拌头材料,受摩擦搅拌力逐渐减弱,产热量降低,材料流动受阻。
4. 结论
1) 基于CFD理论建立lFSW过程有限元模型,模拟预测材料流动轨迹结果与实验相吻合,搅拌头及其附近区域的材料流动方向与搅拌头的旋转方向一致,AS和RS的材料均绕着搅拌头旋转,并在返回侧的相应位置释放。
2) 在FSW过程中,当搅拌头的旋转速度增加时,搅拌头附近区域材料流动更加剧烈;焊接速度的提高对搅拌头及其附近区域材料的流动影响不大。
基金项目
国家自然科学基金:51405310;沈阳航空航天大学大学生创新创业项目:S1701057。