面向轻量化的基座结构优化设计方法

The Structure Optimization of Pedestal for Lightweight

摘要: 基座作为机械结构重要承重件，其强度性能直接关系整机安全。针对筋板式基座结构，其构成件厚度是设计的关键点，以改善基座结构强度、降低重量为优化目标，以基座构成件结构参数为优化变量对基座进行结构优化，计算出较优的基座构成件尺寸参数，保证在满足强度要求的前提下，实现基座轻量化设计。

Abstract: As an important load-bearing part of the mechanical structure, the strength of the pedestal is di-rectly related to the safety of the whole machine. For the stiffened base structure, the thickness of the components is the key point of the design for the stiffened pedestal structure. The optimization goal is to improve the structural strength of the pedestal and reduce the weight of the pedestal. Taking structural parameters of the pedestal components as optimization variables, the pedestal structure is optimized and the better parameters of the pedestal components are obtained. The weight of the pedestal is reduced on the premise of meeting the strength requirements.

1. 引言

随着机械系统的大型化、重型化发展，承重件的承载能力与制造成本不断升高。基座作为重要的承载结构，负担所承载的零部件重量，并将重量传递给土建基础，其结构设计在机械结构中占重要地位。由于机械系统重型化的发展，基座承载能力的提升直接造成制造成本的升高，基座制造经济成本和功能的平衡, 在很大程度上取决于基座承重结构的构成及构成件设计方面。

目前在承重件结构设计构成方面，部分学者针对承载件的结构样式进行了改变：周博学者针对某船波浪补偿起重机基座结构，对比了基座两种加强样式，对基座结构设计提供了指导意见 [1] ；汤卫民等学者针对绞盘基座结构样式，提出了不同的改进方案 [2] 。上述研究主要集中在结构样式的改变，提升承载能力、降低制造成本的同时，很少直接针对构成件细节进行优化设计。目前在承载构成件设计优化方面，部分学者对承载件主要参数进行了优化设计 [3] [4] [5] ，在保证结构安全性能的基础上，使整体零件轻量化。结合目前基座构成件细节优化设计，本文以筋板式基座为研究对象，在传统基座结构构造形式的基础上，针对筋板式基座构成件几何形体相关参数，在满足基座强度使用要求的前提下，理性化地降低基座重量，节约成本。

2. 基座参数化模型构建

筋板式基座结构如图1所示，主要由上板、下板、筋组成。

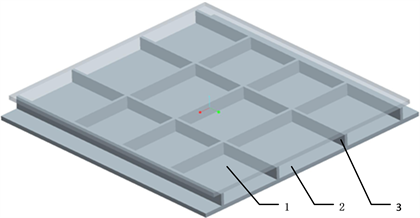
Figure 1. The stiffened base structure. 1—The upper plate; 2—The lower plate; 3—Rib

图1. 筋板式基座结构。1——上板；2——下板；3——筋

筋板式基座强度性能主要由构成件几何参数决定，由于基座强度与重量指标均取决于构成件厚度，因此选取上板厚度、下板厚度与筋厚度为优化参数，由此确定优化变量，如图2所示。

基于基座空间尺寸约束及其构成件内部尺寸关联性，确定各优化参数变化区间及相关参数约束条件。基座优化参数设定为：

$X=\left[X1X2X3X4X5\right]$ (1)

式中：X1——上板厚度；

X2——下板厚度；

X3——筋1厚度；

X4——筋2厚度；

X5——筋3厚度；

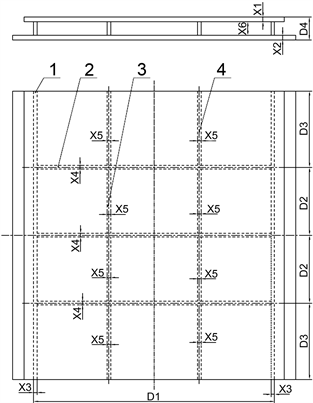
Figure 2. The optimization parameters of the base components. 1—Rib 1; 2—Rib 2; 3—The first part of rib 3; 4—The second part of rib 3

图2. 基座构成件优化参数。1——筋1；2——筋2；3——筋3段1；4——筋3段2

针对各构成件参数之间的关联性，优化参数的改变驱动结构其它参数发生变化，并且基座连接承载件及土建，基座负载件与土建之间具有安装空间尺寸要求，因此基于基座几何参数关联性及空间尺寸安装要求，各优化参数的变化需满足以下约束条件：

$\{\begin{array}{l}{L}_2+2\times X3=D1\hfill \\ L_{3-1}+X4=D2\hfill \\ L_{3-2}+X4/2=D3\hfill \\ X1+X2+X6=D4\hfill \end{array}$ (2)

式中，L2——筋2长度；

L3-1——筋3长度1；

L3-2——筋3长度2；

D1——常量，下板螺栓安装预留空间尺寸约束；

D2——常量，筋2安装空间尺寸约束；

D3——常量，筋2安装空间尺寸约束；

D4——常量，基座负载件与土建安装空间尺寸约束;

X6——筋高度。

综合考虑基座接口空间、基座腐蚀、基座安装空间等因素，设计各构成件厚度变化阈值，以确定各优化参数最大与最小尺寸约束条件，各优化参数尺寸阈值设计如表1所示。

Table 1. Threshold of optimization parameters

表1. 优化参数约束阈值

由此，从基座构成件角度出发，选取构成件几何厚度为优化参数，并设置关联约束条件保证基座参数取值的合理性，完成基座参数化模型构建。

3. 基座结构优化

基于基座参数化模型，面向基座安全性能，选取基座结构优化目标对优化参数进行寻优，实现基座结构优化。

3.1. 基座优化目标选取

基座设计是否合理取决于其功能性及经济性，为满足基座承载功能性要求，基座结构需满足使用强度要求，因此从基座强度性能及经济性能筛选基座优化目标。

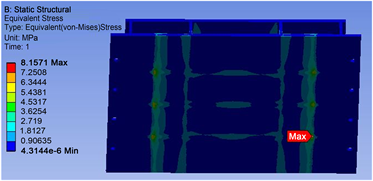
在基座强度性能方面，基座工作过程中承受了所承载件的主要重量，底部两侧由土建支撑，其承载能力主要由静强度保证，因此在设计过程中必须对其进行静力学分析，从而找出基座的薄弱部位表征指标，以此为依据确定优化目标。通过静力学分析，基座结构等效应力分布云图如图3所示。

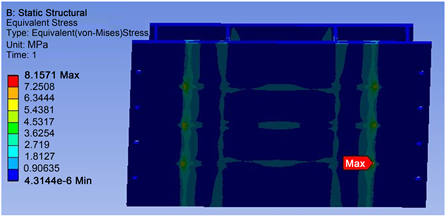
Figure 3. The equivalent stress of the base

图3. 基座应力分析图

由图3可知，结构最大等效应力位于筋2与下板、基座与支撑土建连接处，最大等效应力数值为8.1571 MPa，初步设计余量过大。

由结构静力学分析可知，最大等效应力最大值表征基座薄弱部位的强度性能是否达标，因此选取最大等效应力为优化目标之一。

在基座经济性能方面，由图3可知，基座构成件初步设计厚度值虽然满足强度要求，但基座整体重量为3353.1 kg，整体结构过于笨重，制造成本较高，由于强度设计余量较大，因此可对基座结构进行减重设计。在基座设计过程中，降低基座重量往往会削弱结构强度，基座构成件厚度参数优化过程需均衡考虑结构强度与重量，由此选取基座整体重量为优化目标之一。

从基座功能性及经济性角度出发，在保证安全性能的基础上，为了实现更理想的工程造价，以降低基座结构最大等效应力与重量为优化设计目标，确定优化目标函数为：

$\min \{\begin{array}{c}f1\left(X\right)f1\left(X\right)<\left[\sigma \right]\\ f2\left(X\right)\end{array}$ (3)

式中， $f1\left(X\right)$ ——基座最大等效应力；

$\left[\sigma \right]$ ——结构许用应力；

$f2\left(X\right)$ ——基座整体重量。

3.2. 基座结构优化

目前智能算法在工程领域应用越来越广泛 [6] [7] [8] [9] [10] ，ANSYS Workbench优化模块集成了常用的智能算法，因此本文在ANSYS Workbench优化模块平台下对基座结构进行优化。由于基座优化参数与优化目标存在非线性映射关系，直接对其进行优化较困难，基于ANSYS Workbench优化模块，首先抽取样本点建立基座设计参数与优化目标的预测模型，以此进行后续优化。

针对各优化参数及取值范围，由于筋、上板与下板几何厚度值具有不确定性，因此采用随机均布采样的方式在各参数取样范围内选取样本点，并以离散量矩阵的形式表征不同参数组合的基座样本模型，以此作为基座优化预测模型的训练样本及测试样本。

基于表1中各优化参数变化阈值，对五个优化参数采用拉丁超立方方法抽样出500个离散量作为样本点输入值，并组合成矩阵形式表征各参数在对应样本点下形成的基座结构参数模型，在相同边界条件下通过ANSYS计算各输入样本点对应的基座结构最大等效应力与重量值，作为各样本点的输出值，以此实现优化输入样本与优化输出样本的构建。

由于神经网络具有结构简单、可调整的参数多，并且可操作性好等优点 [11] [12] [13] ，因此选取神经网络智能算法构建基座优化输入与输出预测模型。在ANSYS Workbench优化模块下，针对500个样本数据，选取神经网络方法建立优化参数与输出目标之间的映射关系，完成预测模型的构建。

基于预测模型，优化参数对基座结构最大等效应力、重量指标的灵敏度如图4、图5所示。

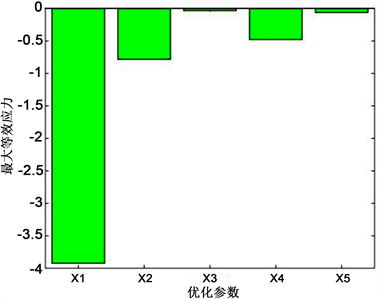
Figure 4. The sensitivity of the optimization parameters to the max equivalent stress

图4. 优化参数对最大等效应力灵敏度

经过图4、图5灵敏度分析结果对比，可以看出上板厚度、下板厚度与筋2厚度对结构强度影响较大。

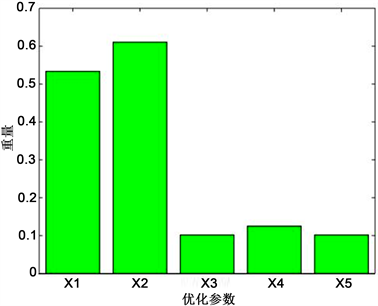
Figure 5. The sensitivity of the optimization parameters to the mass

图5. 基座应力分析图优化参数对重量灵敏度

由于基座结构优化属于多目标优化问题，由图4与图5同样可以看出基座重量与强度两目标之间是相互冲突的，在满足重量最轻的同时，基座强度性能由于受结构重量的降低会变差。因此基于已建立的预测模型，选用多目标遗传算法对基座各构成件厚度进行优化，其中种群大小设置为100、最大进化代数设置为200，优化结果如表2所示。

Table 2. The optimization solutions

表2. 优化解集

基于ANSYS对优化后的基座结构进行分析，表2优化参数组合成的基座结构实际最大等效应力值为20.278 MPa，最大等效应力预测误差为0.094；基座实际重量为1528.107 kg，结构重量预测误差为0.000135，经过对比，误差满足要求。

3.3. 基座结构优化结果对比

为满足加工制造要求，对优化解集参数进行圆整作为基座设计参数，优化后基座结构应力分布如图6所示，与初步设计的基座结构对比如表3所示。

(a) (b)

Figure 6. The equivalent stress of the base. (a) The non-optimized base; (b) The optimized base

图6. 基座等效应力分布云图。(a) 未优化基座；(b) 优化后基座

由图6可以看出，通过与初步设计的基座结构进行对比，优化后基座最大等效应力集中区域位置未发生变化，最大等效应力数值为19.323，重量为1515.93 kg。

Table 3. The comparison of the max equivalent stress and the mass

表3. 最大等效应力与重量结果对比

通过表3对比结果可以看出，优化后基座结构最大等效应力仍在强度要求范围内，重量降低了54.8%，实现了基座轻量化设计。

4. 结论

本文以筋板式基座为研究对象，构建基座参数化模型表征基座构成件几何尺寸，以基座结构重量最轻、强度最高为目标函数，基于ANSYS优化模块下的智能算法对基座构成件尺寸进行优化设计。计算结果表明筋板式基座结构初始设计时虽然能满足强度要求，但主要构成件设计尺寸留有很大的余量，基座整体结构过于笨重，经过优化设计，在基座结构满足在强度要求基础上，降低了结构重量，权衡了基座结构强度与重量，为基座结构细节优化设计提供了参考。

NOTES

^*通讯作者。