基于VLBM方法研究柴油机多孔微粒捕集器渗流机理

Study on Seepage Mechanism of Diesel Porous Particulate Filter Based on VLBM

摘要: 柴油机依靠其良好动力性和经济性的优势，自问世以来，便在车辆、船舶等动力装置得到广泛应用。与此同时，柴油机微粒排放物也带来严重的污染问题，引起人们的广泛关注。本文采用体积格子玻尔兹曼方法(VLBM)，在孔隙尺度上，论述了多孔介质过滤体结构和进口速度对捕集器通道模型内流场的影响，为柴油机微粒捕集器的数值模拟研究提供一个新的思路。结果表明，孔隙度越大，微粒捕集器孔道模型中的流场越稳定，进出孔道压差越小；相比于孔隙度，过滤体厚度对流场影响较小，然而过滤体厚度越大，进出口孔道压差越大；进口速度越大，流场越紊乱，压差越大。

Abstract: Diesel engines have been widely used in vehicles, ships and other power plants since they were invented because of their good power and economic advantages. At the same time, diesel particu-late emissions also bring serious pollution problems, causing widespread concern. In this paper, the influence of porous media filter structure and inlet velocity in the flow field of the trap passage model is discussed on the pore scale by using the volumetric lattice Boltzmann method. It provides a new idea for numerical simulation of diesel particulate trap. The results show that the larger the porosity is, the more stable the flow field is and the smaller the pressure difference between inlet and outlet is. Compared with porosity, the thickness of the filter has less influence on the flow field. However, the greater the thickness of the filter, the greater the pressure difference between the inlet and outlet channels is. The larger the inlet velocity is, the more turbulent the flow field is, the greater the pressure difference is.

1. 前言

因为柴油机具有优良的经济性、动力性、可靠性，在汽车工业逐渐得到广泛的应用。研究表明，柴油机 、 以及 排放物远低于同等功率汽油机，但是微粒排放物却是汽油机的30~80倍，严重污染环境并危害人类健康 [1] [2] [3] 。控制微粒排放物成为了研究热点，目前，微粒捕集器(DPF)凭借较高的捕集效率、工作可靠、成本低廉、设备相对简单、排气阻力较低等特点，被公认为解决柴油机微粒排放问题最有效的手段之一。利用柴油机台架实验往往会遇到消耗大、周期长等问题，因此进行数值模拟研究减少试验工作量具有一定的意义 [4] 。微粒捕集器系统空间上具有多个尺度的特性，数值模拟方法从尺度上可以划分为三类：研究整个过滤器流场、研究过滤器孔道流场和研究过滤体流场 [5] 。目前国内微粒捕集器模拟研究大多集中在第一类，基于宏观连续介质假设建立相关数学模型。相关实验表明：微粒越小，对人体危害越严重。微粒粒径越小，越容易突破鼻腔以及呼吸道的阻碍到达肺部，粒径小于2.5微米的微粒可直接到达肺泡内，导致心肺功能障碍的疾病 [6] ，柴油机产生的微粒排放物的粒径往往处于微米级别，因此，从孔隙尺度研究流体具有一定意义 [7] 。体积格子Boltzmann方法是一种在传统LBM方法基础上发展起来的新型介观数值模拟方法。2014年Yu等人提出VLBM并采用该方法进行了注射器内流体、2D蠕动流和3D管道流模拟研究，模拟结果与理论结果吻合 [8] 。2017年An等人采用VLBM对数字岩心中的流体流动进行了模拟研究 [9] 。本文基于VLBM研究过滤体在不同孔隙度、不同厚度以及过滤器不同进口速度下对壁流式微粒捕集器流场的影响，为将来在孔隙尺度模拟研究微粒捕集器提供一定参考。

2. 物理模型

壁流式微粒捕集器过滤体通常分成蜂窝陶瓷、泡沫陶瓷及陶瓷纤维这三种多孔介质材料，其中壁流式蜂窝陶瓷微粒捕集器采用低热膨胀系数堇青石材料，过滤效率较高，能达到90%以上。结构如图1所示，其结构特点为，捕集器两端面上相邻孔道交替封堵，相邻孔道壁面为多孔介质过滤体，排气从孔道左端进入，通过多孔介质过滤体，然后从右端流出，在此过程中颗粒物被过滤体捕获 [10] 。

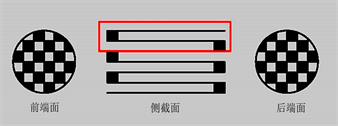
Figure 1. Wall flow particulate trap structure

图1. 壁流式微粒捕集器结构

本文中选取图1中红框内一组进排气孔道为研究对象，利用随机配置的方法人工构造一种多孔介质模型，首先在网格中随机选取一个单元，然后以一定概率将其置为固体单元，并重复上述过程直至满足事先设定的孔隙率。图2为孔隙率为0.4的二维多孔介质模型。

Figure 2. Two dimensional model of porosity 0.4

图2. 孔隙率0.4的二维模型

将这一方法类推到三维中，可以得到三维多孔介质模型，如图3所示。

Figure 3. There dimensional model of porosity 0.4

图3. 孔隙率0.4的三维模型

模拟中，采用的流体密度为0.64 kg/m³，粘度为2.87 × 10⁻⁵ m²/s，计算域的大小为200 × 50 × 100，格子分辨率为1 × 10⁻⁵ m。在进行过滤体对流场影响的研究中，进口速度为5 m/s，出口均为标准大气压。

3. 模拟方法

3.1. 方法概述

Yu等人近年来提出了体积格子玻尔兹曼方法(VLBM)，并通过验证证实VLBM方法对于解决如多孔介质、移动边界等复杂的结构模型具有一定的优势。通过引入一个定义为固体基质部分占单元格体积比例的体积参数 $P\left(x,t\right)$ 来描述多孔介质中基质与孔隙部分，并将多孔介质中单元格分成三类：1) 固体单元格 $\left(P\left(x,t\right)=1\right)$ ；2) 流体单元格 $\left(P\left(x,t\right)=0\right)$ ；3) 边界单元格点 $\left(0<P\left(x,t\right)<1\right)$ ，如图4所示。

Figure 4. Cell classification

图4. 单元格分类

与传统格子玻尔兹曼方法(LBM)假设流体粒子处于格点不同，在VLBM中，流体粒子均匀分布在格子单元格内，并通过体积参数 $P\left(x,t\right)$ ，使得VLBM公式具有自正则的性质且严格满足质量守恒。此外，VLBM也同时具备传统LBM物理意义清晰、边界条件处理简单、程序容易事实、并行性能好等特点 [8] 。

3.2. 方法介绍

目前，格子玻尔兹曼方法中单松弛模型是至今引用最为广泛的LBE模型，其中由Qian等人提出的DnQb (n为空间维数，b是离散速度数)最具代表性 [11] 。如图5(a)所示的D2Q9的格子模型中，每个格子的体积大小可以表示为 $V=\left(l^D\right)$ 。流体粒子位于格点 $x$ ，函数 $f_i\left(x,t\right)$ 指的是粒子密度分布函数。经过一个时间步 $\Delta t$

(a) (b)

Figure 5. (a) Traditional LBM lattice model; (b) VLBM lattice model

图5. (a) 传统LBM格子模型；(b) VLBM格子模型

之后，原本位于格点 $x$ 处的流体粒子，相互碰撞后迁移到临近的 $x+e_i\Delta t\left(i=1,\cdots ,b\right)$ 格点处。如图5(b)所示，在VLBM中，假设流体粒子均匀地分布在单元格中。类似于粒子分布函数 $f_i\left(x,t\right)$ ，引入函数 $n_i\left(x,t\right)$ 来表示在时间t，占据 $x$ 单元格，具有离散速度 $e_i$ 的粒子分布函数 [9] 。根据体积参数 $P\left(x,t\right)$ 的定义，可以得到 $f_i\left(x,t\right)$ 和 $n_i\left(x,t\right)$ 的关系如下式：

$n_i\left(x,t\right)=f_i\left(x,t\right)\times \left[1-\text{P}\left(x,t\right)\right]\times V$ (1)

类比于传统的格子玻尔兹曼方程，可以得到VLBM的演化方程：

$n_i\left(x+e_i\Delta t,t+\Delta t\right)=n_i\left(x,t\right)+{\Omega }_i\left(x,t\right)$ (2)

其中 ${\Omega }_i\left(x,t\right)$ 为碰撞算子，由粒子碰撞过程中动量、动能相互交换产生，根据BGK近似，通过引入一个单松弛时t，可以将其表示为：

${\Omega }_i\left(x,t\right)=-1/\tau \left[n_i\left(x,t\right)-n_i^{eq}\left(x,t\right)\right]$ (3)

式中的 $n_i^{eq}\left(x,t\right)$ 为平衡态分布函数可以表示为：

$n_i^{eq}\left(x,t\right)=N\left(x,t\right){\omega }_i\left[1+\frac{e_i\cdot u}{c_s^2}+\frac{{\left(e_i\cdot u\right)}^2}{2c_s^4}+\frac{{\left(u\right)}^2}{2c_s^2}\right]$ (4)

其中 $N\left(x,t\right)={{\displaystyle \sum }}^{\text{}}{n}_i\left(x,t\right)$ ，为当前单元格密度， ${\omega }_i$ 为权重系数， $c_s$ 为格子声速。和传统LBM相同，在VLBM一个时间步的演化过程中，分成碰撞过程和迁移过程两部分进行，将碰撞后的粒子分布函数表示为 ${n^{\prime }}_i\left(x,t\right)$ ，碰撞步方程为：

${n^{\prime }}_i\left(x,t\right)=n_i\left(x,t\right)+{\Omega }_i\left(x,t\right)$ (5)

流体粒子碰撞过后，将会迁移到邻近的单元格中，这一过程称为迁移过程。迁移过程是VLBM适用于处理复杂几何模型的关键所在，将固体边界的反弹边界格式融入在迁移步之中。由图6可以看出，11、5、12三个方向的粒子密度分布函数是由两部分组成，实线表示由下方单元格迁移过来的粒子密度分布函数，而虚线则指的是本单元格14、6、13方向的粒子密度分布函数迁移到下方单元格与固体基质发生碰撞后反弹回来的密度分布函数。根据这一思路，将迁移后的粒子分布函数用 ${n^{″}}_i\left(x,t+\Delta t\right)$ ，则迁移步的方程可以表示为：

${n^{″}}_i\left(x,t+\Delta t\right)=\left[1-P\left(x,t\right)\right]{n^{\prime }}_i\left(x-e_i\Delta t,t\right)+P\left(x-e_{{}_{i*}}\Delta t,t\right){n^{\prime }}_{i*}\left(x_i,t\right)$ (6)

其中i^*为i的反方向，即 $e_{{}_{i*}}=e_i$ 。

Figure 6. Sketch map of streaming steps

图6. 迁移步示意图

流场的宏观参数密度、速度以及压强可由密度分布函数统计得出：

$\rho \left(x,t\right){{\displaystyle =}}^{\text{}}{\displaystyle \sum n_i}\left(x,t\right)/\left[1-P\left(x,t\right)\right]$ (7)

$u\left(x,t\right)={\displaystyle \sum e_i{n}_i}\left(x,t\right)/{\displaystyle \sum n_i}\left(x,t\right)$ (8)

$p\left(x,t\right)-p_0=c_s^2\left[\rho \left(x,t\right)\right]-{\rho }_0$ (9)

其中 $p_0$ 和 ${\rho }_0$ 分别为初始压力和初始密度。

4. 结果讨论和分析

本文分别从三个方面讨论分析了柴油机壁流式微粒捕集器孔道模型在不同条件下流场的变化情况，为在孔隙尺度下模拟微粒捕集器流场提供一定参考。

4.1. 过滤体孔隙度对流场的影响

选取了0.3到1之间不同孔隙度的模型，分别做了模拟，图7为孔隙度为0.4、0.6、0.8以及1的孔道模型流线图。从图中可以看出，在孔隙度为1的情况下，大部分流体从进口直接流向出口，而有多孔介质存在的模型中，流线的形状发生改变。流体在多孔介质层中的流速普遍高于孔道内流速，这是由于孔隙较孔道空间狭窄，流速上升，符合实际情况。随着孔隙度的增加，流场内流线逐渐平缓，当孔隙度达到0.8以上时，孔道内流线基本与空腔流线接近，只在多孔介质层发生些许弯折。为进一步说明这一现象，引入流场中各个格点处流速标准差以及如图8所示的模型中X方向中各个截面流速的最大值两个参数。标准差旨在表征流场内各点流速数值的离散程度，然而标准差大的情况下，若流场流速均匀增大则流场依然相对稳定，因此引入X方向中各个截面流速的最大值进行补充说明。

Figure 7. Streamline of channel under different porosity

图7. 不同孔隙度下孔道的流线图

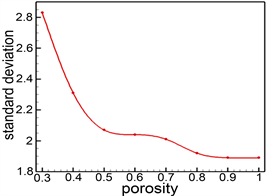
标准差分析结果如图9(a)所示，总体趋势随着多孔介质孔隙度逐渐增加，标准差逐渐下降，孔隙度从在0.3到0.5之间，标准差急剧减小；孔隙度达到0.8以后，标准差基本与空腔一致。图9(b)中，随着孔隙度的逐渐增加，曲线的震荡程度逐渐变弱，当孔隙度0.8以后，曲线与空腔曲线基本重合。由此可见，在孔道模型中，流场的紊乱程度与多孔介质层的孔隙度大小密切相关，当孔隙度较小时，流场较紊乱；孔隙度较大时，流场相对平稳；当孔隙度达到0.8以后，多孔介质层对流场的影响很小。

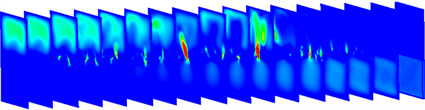
Figure 8. Flow fields in X direction at 0.4 porosity

图8. 孔隙度为0.4时X方向各截面流场

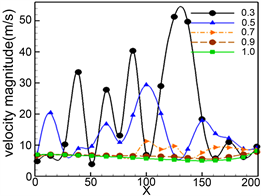(a)(b)

Figure 9. (a) Standard deviation of different porosity; (b) Maximum velocity of cross section in X direction with different porosity

图9. (a) 不同孔隙度标准差；(b) 不同孔隙度X方向截面最大流速

压力损失是柴油机微粒捕集器的主要工作参数之一，对汽车的动力性以及燃油经济性具有重要的影响，柴油机微粒捕集器的优化设计主要就是在保证捕集性能的前提下，降低压力损失 [12] 。因此，本文讨论分析了在不同孔隙度的情况下，进口孔道和出口孔道的压差，结果如图10所示。从图中可以看出，当孔隙度为0.3时，进出口孔道压差接近2000 pa；孔隙度大小从0.3增大到0.5时，进出口孔道压差急剧减小；孔隙度增大到0.8以后，进出口孔道压差基本与空腔相同。压差的变化趋势与流场平稳程度的变化趋势基本保持一致。

Figure 10. Pressure difference between inlet and outlet under different porosity

图10. 不同孔隙度下进出口孔道压差

4.2. 过滤体厚度对流场的影响

相关研究表明，过滤体的厚度对压力损失大小有一定影响，过滤体厚度增大会增加压力损失 ^[11] 。本文中，首先选取了孔隙度为0.4，过滤体具有不同厚度的模型进行了模拟，结果如图11所示。当加入5层多孔介质过滤体后，流线形状发生改变，但是随着多孔介质过滤体厚度的继续增加，模型内流线的紊乱程度并没有显著变化。我们考虑到可能是因为多孔介质孔隙度大小在影响流线形状中，较多孔介质层厚度起更大的作用，当孔隙度较小时，即使过滤体厚度较小，依旧对流场造成较大影响。在下一步工作中，选取了孔隙度为0.8具有不同厚度过滤体的模型进行了研究，模拟结果如图12所示。由于过滤体孔隙度较大，即使加入5层多孔介质后，与空腔相比，流线的形状变化不大。当多孔介质加厚以后，孔道内的流线变化依旧不大。图13(a)，图13(b)分别是孔隙度为0.4和0.8的情况下，过滤体不同厚度时，X方向上各个截面最大速度。从图中可以看出，孔隙度为0.4的情况下，随着过滤体厚度的增加，曲线震荡程度变化不大；孔隙度为0.8时，过滤体在不同厚度的情况下，曲线一直保持相对平缓。图14(a)，图14(b)分别为孔隙度为0.4和0.8时，进出口孔道在不同厚度的情况下的压差。当孔隙度为0.4时，过滤体厚度从5层增加到

Figure 11. Streamlines of different thickness at porosity 0.4

图11. 孔隙度0.4时孔道在不同厚度流线图

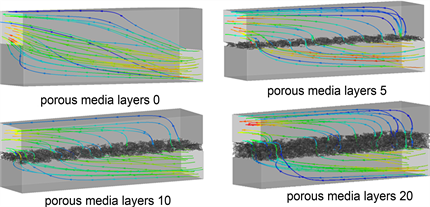
Figure 12. Streamlines of different thickness at porosity 0.8

图12. 孔隙度0.8时孔道在不同厚度流线图

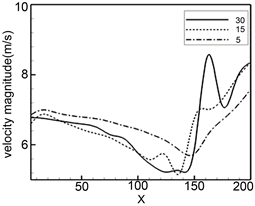(a) (b)

Figure 13. (a) The maximum velocity of cross section in X direction at porosity 0.4; (b) the maximum velocity of cross section in X direction at porosity 0.8

图13. (a) 孔隙度为0.4时X方向截面最大流速；(b) 孔隙度为0.8时X方向截面最大流速

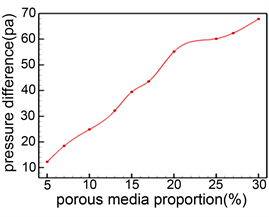(a) (b)

Figure 14. (a) Pressure difference between inlet and outlet at porosity 0.4; (b) pressure difference between inlet and outlet at porosity 0.8

图14. (a) 孔隙度为0.4时进出口孔道压差；(b) 孔隙度为0.8时进出口孔道压差

30层的过程中，进出口孔道压差从200多pa一直上升到3000多pa。当孔隙度为0.8时，随着过滤体厚度的增加，压差也随之上升。由于孔隙度较大，与孔隙度为0.4的情况相比，进出口孔道之间的压差要小很多，即使当厚度达到30层，压差也仅仅只有60多pa。综上所述，多孔介质过滤体厚度大小对微粒捕集器流线形状影响较小，但是随着过滤体厚度的增加，进出口孔道压差随之上升，因此在微粒捕集器结构的设计优化中，也应该考虑到过滤体厚度。

4.3. 进口速度对于流场的影响

柴油机在不同工况下的排气速度不同，因此研究不同速度下，微粒捕集器内流场的变化也具有一定的意义。图15为不同进口速度时，孔道模型的流线图。从图中可以较为直观的看出，随着进口速度地不断增加，微粒捕集器孔道模型中的流线逐渐紊乱。图16中标准差与进口速度的关系进一步验证了这一结论。随进口速度的增大，孔道内速度的标准差也越来越大。图17为不同进口速度下，微粒捕集器进出口孔道间压差，进口速度越大，孔道间的压差越大，当进口速度达到7 m/s时，压差接近2000 pa。

Figure 15. Streamline under different inlet speeds

图15. 不同进口速度下孔道流线图

Figure 16. Standard deviation at different speeds

图16. 不同速度下的标准差

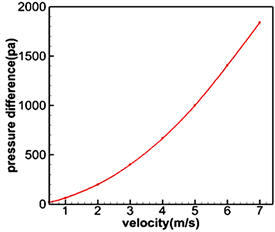
Figure 17. Pressure difference under different inlet speeds

图17. 不同进口速度下孔道间压差

5. 总结与展望

本文中利用体积格子玻尔兹曼方法，一种在传统格子玻尔兹曼基础上发展出来的适用于多孔介质、移动边界等具有复杂边界的模型新型介观数值模拟方法。在孔隙尺度上，模拟研究简单柴油机微粒捕集器在过滤体不同孔隙度、不同厚度以及不同进口速度的情况下流场的变化。当过滤体孔隙度、进口速度增大时，流场趋于紊乱，进出口孔道压差也越来越大。相比于孔隙度，过滤体厚度对流场影响较小，但是进出口压差随着厚度增大而上升。王鹏伟等人开展的多孔介质微流动特性的实验研究中，通过微粒填充的方式构建了多孔介质模型，利用Micro-PIV技术(微流体粒子图像测试技术)测量了微珠多孔介质模型在不同孔隙度、不同流量时的流场。实验结果表明多孔介质层压差随着孔隙度的增大而增大，与流量成线性关系 [13] ，本文中的模拟结果与这一结论一致。因此，基于VLBM对于微粒捕集器的模拟研究可以提供一个新的思路参考。

基金项目

课题受国家自然科学基金(编号U1262109, 51476145, 51476146)资助。

NOTES

^*通讯作者。