1. 引言
相干合成技术是指通过锁定多组单元激光器间相位差,使输出激光在作用目标处形成稳定的干涉效果,以提高远场的能量集中度。该方案能够在实现功率扩展的同时保证整个系统的光束质量,是融合现阶段各种成熟技术实现高亮度激光器的有效途径 [1]。
激光光束相干合成是实现高功率、高能量、高光束质量激光输出的重要技术手段,为当前国内外研究的热点。光束相干合成与非相干合成有很多重要的区别,其中之一是在相干合成中实现了各子束间的相位锁定,即相干合成是各子束相位锁定输出的结果,即“锁相”输出。而激光锁模技术是一种实现窄脉宽输出的激光调制技术,锁模的本质也是实现不同纵模间的相位关系 [2] [3]。
本文从二者的物理基础出发分析了激光光束相干合成与激光锁模技术的关系,比较了二者的异同,阐述了二者的技术手段,分析了互相之间的借鉴意义。意在增强对相干合成和锁相技术的理解,同时对相干合成技术的实现手段进行新的探索。
2. 物理基础
2.1. 相干合成的物理基础
以平面矩形光为例,其远场分布为 [4]
(1)
则N束光束合成中,
(2)
其中
为各光束近场之间的间距,
为近场光束间距在远场引入的相位调制量。
(3)
光束合成过程,
,式中I1,I2是两子束的强度,
,
是两光束的相位差,因此相位差是影响相干合成效果的一个关键参数。
光束相干合成要求各子束的相位、偏振态和频率的高度一致,在光源确定的情况下,控制其相位成为了最关键的技术。图1显示了4束激光在近场紧凑排布时,相干合成与非相关合成的区别,明显看出了相干合成后的光束能量(功率)更为集中 [5]。
 (a)
(a)  (b)
(b)  (c)
(c)
Figure 1. Difference between non-coherent synthesis and coherent synthesis: (a) Near-field arrangement; (b) Non-coherent combined far field; (c) Coherent combined far field
图1. 非相干合成与相干合成的区别:(a) 近场排布;(b) 非相干合成远场;(c) 相干合成远场
2.2. 激光锁模的物理基础
在自由振荡激光器谐振腔中,满足增益条件的纵模很多,它们彼此不相关,频率不同,初始相位不同,导致输出激光的功率无规则起伏,若可以设法控制谐振腔的参数,使各纵模的初位相彼此相关,若使得相邻两纵模间的初始位相差均保持为某一常数,这样激光器的输出特性便会发生显著的变化,这个过程就是锁模 [6] [7]。
设激光输出2N + 1个纵模,则它的表达式为
(5)
(6)
式中
为各个模式的振幅;
为初始的角频率,
为初始的角频率,
为固定的角频率差,
为固定的相位差。
输出光强为
(7)
当各模式不相干时,输出的功率就是各模式功率的迭加,即
(8)
若各模式相位锁定为
时,光强最大。最大光强(脉冲峰值功率)为
(9)
锁模后的峰值功率比未锁模时提高了(2N + 1)倍。
图2显示了锁相前后输出功率的变化,锁相前各模式间相位没有关系,各模式波强随机迭加,时间上显示了光强分布的随机变化;锁相后,各模式间的相位固定,实现了相干迭加,从时间上看功率输出变成了周期性的短脉冲输出,且峰值功率显著增强 [6]。


Figure 2. (a) Output without mode-lock; (b) Output with mode-lock
图2. (a) 锁模前的输出;(b) 锁模后的输出
2.3. 相干合成与激光锁模的异同
从上面的分析可以看出,光束相干合成和激光锁模最大的相同点是,均是通过对各分量相位锁定从而达到能量(功率)集中的目的。
而它们的区别则是
1) 相干合成在空间上实现了能量的汇聚;
激光锁模在时间上实现了能量的汇聚。
2) 相干合成针对同一频率的光束进行相位锁定;
激光锁模则是对不同频率光波进行相位锁定。
3) 相干合成通常针对谐振腔外的光束进行锁相;
激光锁模则是针对谐振腔内的光波进行锁相。
更通俗的理解,我们可以认为相干合成更多的是对激光横模进行调制,而激光锁模技术则是对激光纵模进行调制。
3. 实现相干合成和激光锁模的技术手段分析
3.1. 实现激光光束相干合成的技术手段
主要是通过对各子束的相位进行调节,使子束间相位差恒定且达最小,此时可实现较好效果。其技术方案按照锁相方法的不同,可以分为被动相干合成和主动相干合成,或者叫被动无源式自调整相干合成和主动有源相位控制相干合成。
1) 被动相干合成通过自组织原理在激光器内部实现多路激光的相位锁定,其实现方式主要有干涉仪方式、非线性自组织方式、倏逝波耦合方式等。往往以复合振荡腔的形式存在。被动式相干合成目前达到的效果不是很好,高能激光系统还比较少见 [8] [9]。
2) 主动相干合成利用一定的控制算法通过相位调制器件在激光器外部实现多路激光的相位锁定,控制方法主要有外差法、自适应锁相法、多抖动法、SPGD算法等 [10] [11]。
主动锁相相干合成一般采用在多路MOPA系统内加入相位调制元件,以实现各分束间相差的实时反馈和校正。目前最为成功的主动锁相相干合成技术应用案例当属Northrop Grumman公司的固体激光合成,实现了10万瓦的连续输出。其合成结构如图3所示 [12] ,其方法为外差法。
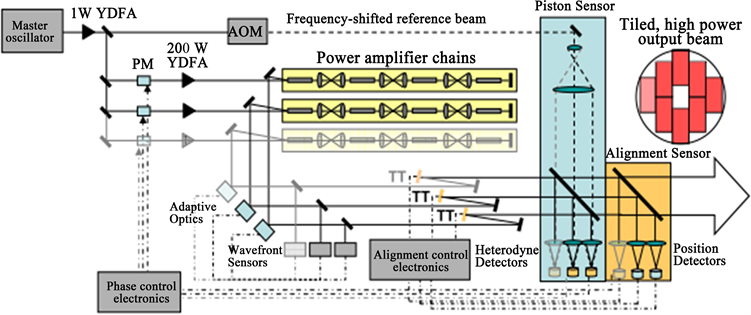
Figure 3. Schematic diagram of active-phase-control beam coherent combination by Northrop Grumman Company
图3. Northrop Grumman公司主动相位控制光束相干合成示意路
3.2. 实现激光锁模的技术手段
目前激光器的锁模方式可分为主动锁模和被动锁模。主动锁模是外加调制器产生振幅或者相位调制,从而实现锁模。被动锁模是在不外加调制器的情况下,通过光纤非线性和强度起伏的共同作用,对腔内损耗进行调制 [13] [14]。
1) 主动锁模技术可以分为振幅调制锁模、相位调制锁模以及同步泵浦锁模三种。对于前两种,通常是在腔内置入适当的损耗调制或相位调制元件并控制调制的频率从而实现模式锁定。常用的调制器件是声光和电光损耗调制以及电光相位调制。如果使用一台锁模激光器作为泵浦源,对另一台锁模激光器进行泵浦,通过控制谐振腔内的激光增益,来实现锁模脉冲的输出,这种方法则是同步泵浦锁模方法 [6] [7]。
2) 被动锁模技术。被动锁模技术的种类很多,常用的有自锁模(克尔透镜锁模)、附加脉冲锁模以及可饱和吸收体锁模等。相比于自锁模,附加脉冲锁模技术能够实现自启动,可适用于大多数的固体激光介质 [6] [7]。
目前最常用的SESAM锁模和克尔透镜锁模都属于被动锁模。
4. 技术借鉴的可能性分析
通过上面的分析,可以看出,不管是相干合成还是激光锁模,都分为主动锁相和被动锁相这两种主要技术。而两者的区别是,对于高能激光系统来说,目前更为常用的是主动锁模技术,而对于短脉冲锁模激光来说,更多的是应用被动式锁模。
4.1. 将成熟的锁模技术应用到相干合成中的可能性
对于高能激光系统来说,主动式相位控制虽然目前取得了一些进展,但其结果复杂、成本高的缺点一直没能得到很好的解决。而现有的被动式合成技术往往需要引入新的耦合腔,这回导致稳定性差、合成效率低、输出功率低等一系列问题。
如果能将激光锁模技术成熟的被动锁相技术引入至高能激光系统,必然会给高能激光系统带来崭新的发展途径。
那么这种方法是否可行,方案应如图4所示,如果在光束相干合成系统里面使用类似于SESAM或
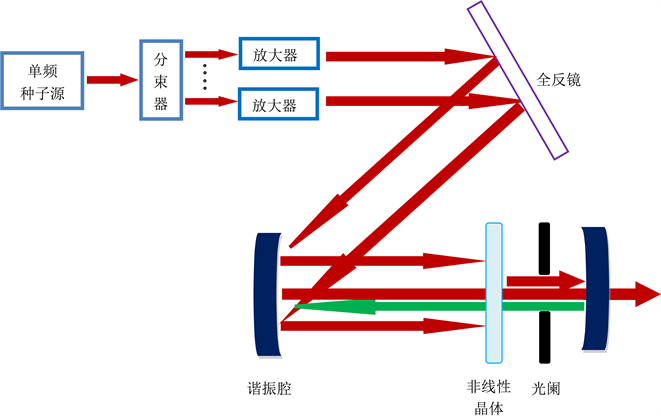
Figure 4. Application scheme of typical passive laser mode-locking technology in laser coherent combination technology
图4. 典型被动激光锁模技术在激光相干合成技术中应用方案图
克尔透镜技术,那么需要光束反复经过这些非线性元件,其最简洁的实现必然是使用谐振腔,这样又回到了老问题上,目前高能激光系统相干合成中没能成熟地使用被动锁相的原因就是因为谐振腔的缺点所导致的。同时,这个时候需要将各分束放大后的高功率激光注入到一个谐振腔里,谐振腔的设计和器件选择也是一个难题。而且更进一步,本来是由于单束达不到高功率,才选用的合束的方法,现在又在谐振腔里合成一束,显然有失妥当。
4.2. 相干合成技术在锁模中应用的可能性
同样,如果能将现有高能激光系统中成熟的主动相位控制技术引入到激光锁模技术中来,也同样可以起到很好的促进作用。
如果要进行像光束相干合成那样的方案,必然要先将各个光束分离开,每一束单独进行控制。现将典型主动相位控制光束相干合成技术的外差法技术应用于激光锁模,其方案设想如图5所示,可以考虑在谐振腔的中间用一个部分反射镜将一部分谐振腔里的光波反射出来,利用色散元件进行分束,然后再分别进行相位控制,但这样,如图5所示,结构将极其复杂,且谐振腔内加入元件将极大地影响谐振腔的性能。
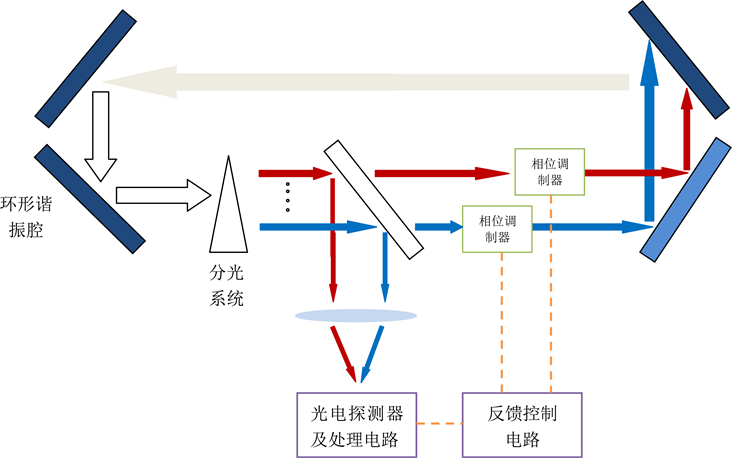
Figure 5. Application scheme of typical active phase control coherent combination technology in laser mode-locking technology
图5. 典型主动相位控制相干合成技术在激光锁模中应用方案图
所以,结合上面的分析可知,如果要使两种技术相互借鉴,需要克服很多问题,其中主要难点有:
1) 激光相干合成的光束在谐振腔外的自由空间,激光锁模针对的光束是在谐振腔内部。若要将成熟的激光锁模技术应用在光束相干合成上面,需要解决如何不在谐振腔里使用被动锁模的技术问题。
2) 激光相干合成的光束在空间上是分离的,激光锁模针对的光束在空间上是纠缠在一起的。若要将成熟的激光相干合成技术应用在激光锁模上面,则需要解决如何分离不同模式的光束,同时加入相位控制单元的问题。
5. 小结
通过本文分析可以得出,从原理上讲激光相干合成和激光锁相均是通过对其分量的相位锁定来获取能量(功率)的集中,其中相干合成在空间上实现了(功率)能量的汇聚,锁模技术在时间上实现了(功率)能量的汇聚。相干合成时对同一频率不同光束的相位锁定,锁模是对不同频率的光波相位的锁定。相干合成可以看成是对激光横模的调制,激光锁模可以看成是对激光纵模的调制。在实现方式上,两者都可分为主动锁相和被动锁相两种方式,其中高能激光系统目前在主动相位控制激光光束合成方面取得了较好的成果,而短脉冲激光实现则更偏重于被动激光锁模。尽管两者在物理基础和技术实现上有着非常多的相似点,但若要进行技术借鉴,则仍然面临着很多较难克服的困难。
基金项目
重庆市教委科技项目(KJ1400532),国家基金预研项目(16XYY32),重庆师范大学博士启动基金(12XLB035)。