1. 引言
现如今钢筋混凝土结构的建筑越来越多,电焊因其操作方便、适应性强、使用灵活和焊接质量好等特点,是建筑施工中使用最为广泛的焊接方法。但在金属焊接过程中,温度高达6000℃以上,容易出现火花,飞溅火星,一旦电焊时存在缺陷、安全可靠性得不到保证,或操作中不注意安全,未合理放置易燃材料,就存在火灾等各类风险,造成巨大的不可逆转的损失 [1] [2] [3] 。在电焊作业过程中主要涉及管理者和电焊工两方主体。管理者负责对电焊作业的过程管理,规定了一切电焊作业需按相关规定的建筑施工电焊作业基本流程执行。电焊工则会持证上岗,按行业规范要求进行电焊作业 [4] [5] 。两个主体互相作用互相影响的结果,是两方主体互相博弈的表现过程。
2. 模型假设与构建
本文研究讨论的是电焊作业过程中两方主体相互影响的情况下各自的行为决策,即管理者是否会按规定严格管理电焊工的操作行为以及电焊工是否会按规范进行电焊操作。通过构建博弈模型分析电焊作业过程中两方主体间的行为决策形成、演化路径以及影响因素,以期为规避特殊工种的作业风险提供理论依据。
假设1:博弈中只存在管理者和电焊工两类博弈主体,管理者的策略集为(严格管理,宽松管理);电焊工的策略集为(规范作业,违规作业)。
假设2:管理者选择严格管理时,其将严格规范电焊作业流程,并配备专有看火人员监督电焊工作业工作,则需花费C。此时,若电焊工违规作业,则其将被处以E的罚款;管理者宽松管理则仅完成相关审批流程,不会额外配备看火人员监督。管理方集团公司会选择内部自查,有发现管理方处于宽松管理状态的概率为θ,且如若工人违规操作,则会对管理方进行惩罚,罚金为T。
假设3:电焊工选择规范作业完成任务,则将获利B;电焊工选择违规作业能在一定程度上提高工作效率α,即获利
。但其可能因此γ的概率罹患职业病而损失P,且若其违规作业且未被发现,则存在β的概率的风险。
结合上述3点假设,构建电焊作业过程中管理者、电焊工两方收益矩阵,ai,bi分别代表管理者、电焊工的收益,如表1所示。
(1)
(2)
(3)
(4)

Table 1. Income matrix of managers and welders during welding operation
表1. 电焊作业过程中管理者、电焊工两方收益矩阵
3. 模型求解
复制动态方程是用来表示某一策略在一个群体中被选择的概率随时间的变化率的动态微分方程。假设管理者选择严格管理的概率是x,选择宽松管理的概率是1 − x;电焊工选择规范作业的概率是y,选择违规作业的概率是1 − y;x、y是关于时间t的函数。其中,
。
3.1. 管理者的复制动态方程
管理者选择严格管理的收益为
(5)
管理者选择宽松管理的收益为
(6)
管理者平均收益为
(7)
根据演化博弈论中关于复制动态方程的定义,如在时刻t管理者选择严格管理策略的概率为x,那么下一时刻x的变化率将与上一个时刻的概率x以及博弈方在该时刻下所对应的策略收益与期望平均收益之间的差值有关,通过公式表达为:
(8)
将式9、10、11带入式12中整理可得管理者的复制动态方程,如式13所示。
(9)
3.2. 电焊工的复制动态方程
电焊工选择规范作业的收益为
(10)
电焊工选择违规作业的收益为
(11)
电焊工平均收益为
(12)
运用复制动态演化方式,将式18、19、20带入整理可得电焊工的复制动态方程,如式21所示。
(13)
4. 模型均衡分析
4.1. 管理者策略均衡分析
当
时,
,这意味着对于所有的x取任何值该博弈都是稳定的。
当
时,令
,可得到
、
两个稳定点。F(x)关于x求导可得
,此时可以分两种情况进行讨论。
1) 当
时,
,
所以
是平衡点,管理者选择严格管理策略是稳定的。
2) 当
时,
,
,所以
是平衡点,管理者选择宽松管理策略是稳定的。
管理者的动态演化趋势如图1所示,以直线
为界,当管理者博弈的初始状态位于直线l1
中,系统经过演化后管理者的最终策略为宽松管理,反之若初始状态位于直线l2中,则管理者的最终策略为严格管理。
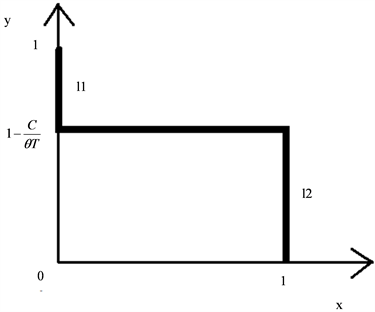
Figure 1. Dynamic sketch of manager strategy evolution
图1. 管理者策略演化动态示意图
4.2. 电焊工策略均衡分析
当
时,
,这意味着对于所有的z取任何值该博弈都是稳定的。
当
时,令
,可得到
,
两个稳定点。 关于y求导可得
,此时可以分两种情况进行讨论。
关于y求导可得
,此时可以分两种情况进行讨论。
1) 当 时,
,
,所以
是平衡点,电焊工选择违规作业策略是稳定的。
时,
,
,所以
是平衡点,电焊工选择违规作业策略是稳定的。
2) 当 时,
,
,所以
是平衡点,电焊工选择规范作业策略是稳定的。
时,
,
,所以
是平衡点,电焊工选择规范作业策略是稳定的。
电焊工的动态演化趋势如图2所示,以直线
为界。当管理者博弈的初始状态位于直线
l3中,系统经过演化后电焊工的最终策略为违规作业,反之若初始状态位于直线中l4,则电焊工的最终策略为规范作业。

Figure 2. Dynamic sketch of welder strategy evolution
图2. 电焊工策略演化动态示意图
综合以上的分析结果,根据博弈两方初始状态所处的空间,本模型两方主体策略的最演化均衡状态如表2所示,其中(x,y)分别代表管理方选择严格管理和电焊工选择规范作业的概率。

Table 2. Evolutionary equilibrium state of two-party principal strategies in welding process
表2. 电焊作业过程两方主体策略演化均衡状态
根据两个不同博弈主体的复制动态方程的分析,整个博弈过程不会收敛到稳定策略集合。这主要原因是电焊作业过程的不同主体博弈过程中,管理者、电焊工选择不同的策略对博弈结果的影响是不同的,只要其中一个主体发生变化,将会导致另一个主体的策略也发生变化,而两个主体的行为又是相互作用和影响的,最终促使两个主体在互相博弈中不断调整选择适合自己的策略,导致整个模型没有稳定的演化策略。
5. 两方演化博弈模型指导意义与安全管理对策
5.1. 两方演化博弈模型指导意义
当管理者选择严格管理付出的成本和宽松管理时面临业主罚款之差与宽松管理时面临的火灾等风险的比值小于电焊工违规作业的概率时,
,即管理者选择严格管理策略。因此,管理者应提高自身管理水平,降低安全管理成本。业主应加大对管理者未进行安全生产管理行为的惩戒力度,加大罚金,最终促使管理者选择严格管理策略。
当电焊工选择违规作业的额外收入、可能罹患职业病的损失和可能面临的管理者对其这种行为的罚款以及管理者宽松管理下其承担的风险之差与管理者宽松管理下其承担的风险的比值大于其规范作业的概率时,
,即电焊工选择规范作业策略。因此,业主应进一步鼓励管理者自觉严格管理,管理者应在一定程度上增加电焊工规范作业的收入,抑制其违规作业的额外收入,并加大管理力度,以促使电焊工自觉在电焊作业中选择规范作业。
5.2. 安全管理对策
基于两方演化博弈模型,本文提出的促进电焊作业施工安全的安全管理对策如下:
1) 健全安全施工管理制度,完善奖惩机制。
从博弈角度上讲,安全施工管理制度就是对管理者以及电焊工的行为进行约束的博弈规则。从一定程度上分析,正是由于现行的安全施工管理制度约束力不强或者存在一定缺陷,才导致了电焊作业过程中两方利益主体博弈的情形出现。要从根本上解决电焊作业安全施工问题,则必须建立更为完善的安全施工管理体系,健全安全施工管理制度,完善奖惩机制。第一,增大电焊工人在规范作业的原则下提高工作效率的激励力度。第二,提高电焊工人违规作业经济成本,降低其违规作业的期望收益,减小其无视安全、违规操作的动机。
2) 优化管理工程师素质,提高监督效率。
本文博弈模型构建的前提是博弈两方不存在任何共谋、勾兑、腐败、契约行为,两方的行为决策均基于各自的期望收益。但现实中往往存在两方共谋、勾兑等违规行为。因此,业主应选择专业管理工程师,发挥其施工安全管理作用。加大对管理工程师宽松管理的惩罚,增加对管理工程师严格管理的激励措施,减少其临界失职概率。管理工程师应注重自身素质的养成,提高自身业务素质和监督技能。
3) 优化施工团队素质,降低施工作业严格管理成本。
管理者严格管理施工人员规范作业是避免施工作业风险的主要手段。因此,管理者应及时对施工管理人员进行严格培训,提高管理队伍的专业素质和管理技能。在规范施工作业管理流程的同时,依靠科学技术,建立施工作业管理信息化系统,通过现代化工具提高安全管理效率,降低施工作业严格管理成本。
4) 加大宣传教育力度,增强风险意识。
在一定程度上,电焊工人违规作业,管理者宽松管理源于其风险意识的淡薄,对违规施工造成安全事故后果的轻估。因此,政府有责任加大安全施工宣传教育力度,增强两方乃至公众的风险意识。在两方规范履行职责的同时,鼓励新闻舆论和公众对管理者及施工人员的违法违规行为进行投诉和举报,实行多主体监督,减少施工安全事故的发生。