1. 引言
随着计算机网络的高速发展,数字图像的信息安全也越来越受到人们的关注。因此,为了保护图像信息不受非法复制、使用和操纵,专家和学者提出了许多加密算法,比如用混沌序列去进行图像的比特位扰乱 [1] [2] 、用混沌序列与图像像素值进行“异或”运算 [3] [4] 、对像素置乱 [1] [5] [6] [7] 等。
在本文,我们提出了一种基于改进的Henon混沌映射 [8] 与Bit位扰乱 [1] [2] 的彩色图像加密算法。文献 [8] 提出了一种改进的Henon映射,增加了序列的复杂性和密钥空间,利用该混沌序列设计了一种新的图像加密算法。该算法融合了两个混沌序列,形成了一个新的随机序列作为关键序列。在文献 [9] 中,一种基于Josephus遍历和广义Henon混沌映射的Bit位图像加密算法被提出,它用Henon映射去驱动改进了的Josephus遍历映射的起始点。文献 [10] 提出了一种基于Ikeda和Henon混沌映射的图像加密算法,首先用Ikeda映射对图像的行和列进行混乱,然后通过Henon映射去更改像素的灰度级。最后再次使用Ikeda映射来改变图像的像素值。基于约束优化算法和Henon映射的级联菲涅耳全息图像加密方案在文献 [11] 中被提出。在文献 [12] 中,一种基于Henon映射和高维块对角矩阵变换的混沌加密算法被提出。它在给定的初始密钥下,在一个环中利用Henon映射构造了两个置换矩阵和一些二维可逆矩阵。在两种类型的平移变换的帮助下,采用置换矩阵对明文图像进行加扰;此外,通过二维可逆矩阵生成高维块对角可逆矩阵,然后通过高维矩阵变换再次对加扰图像进行加密。文献 [13] 为了提高混沌系统中图像加密算法的安全性,提出了一种基于MD5与混沌系统相结合的新算法。基于DCT变换和Henon映射的混沌图像加密在文献 [14] 中被提出。文献 [1] [2] [9] [15] - [21] 都是对Bit位进行置乱,从而达到改变像素值和像素位置的目的;其中文献 [1] [2] [17] [18] [19] [21] 都是使用混沌序列来对Bit位进行置乱,文献 [1] 在进行比特位扰乱时,对二进制数矩阵的行进行了操作;文献 [9] 是使用生成的Josephus遍历映射变量来置换明文图像的像素位置,为了提高安全性,所提出的方法增加了像素比特扩散级;文献 [15] 提出了一种基于超混沌和比特替换的混沌图像加密算法,它使用Hyperhenon映射生成混沌序列,并利用混沌序列的属性来扰乱每个像素的Bit位和像素扩散;文献 [16] 为了提高图像置乱度和安全性,提出了一种基于混合混沌置乱的彩色图像加密算法,将R,G,B三个分量组合成一个整体,利用比特XOR运算以达到扰乱的目的;而文献 [20] 是使用蝶形网络来实现比特置换。文献 [1] [17] [18] 用混沌序列去扰乱像素位置。在本文提出的加密算法中,我们对Henon映射做了进一步的改进,在一定程度上增大了序列的复杂性和密钥空间。
2. 相关知识
Henon映射方程的改进
传统的Henon映射方程:
(1)
当
,
时,Henon系统方程处于混沌状态。如图1所示。
改进后的Henon系统方程:
(2)
当
时,改进后的Henon系统方程处于混沌状态。如图2所示。从图1、图2可以看出图2中处于混沌状态的范围更大。
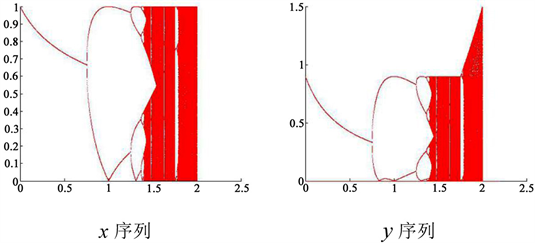
Figure 2. Improved chaotic sequence diagram
图2. 改进后的混沌序列图
3. 算法描述
3.1. 加密算法描述
给定一个
的彩色图像
,加密步骤如下,
Step 1:把彩色图像
的R、G、B三个通道上的矩阵分别取出来,同时把这三个矩阵按行合并成一个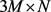 的矩阵,记为
。
的矩阵,记为
。
Step 2:把
转换成一行
列的矩阵
,同时把
转换成二进制数矩阵
。
Step 3:输入初始密钥
;迭代系统(2)
次,产生两条混沌序列
。
Step 4:把混沌序列
和
做如下处理:
(3)
(4)
(5)
(6)
其中
;
为求模运算;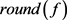 是对
进行靠近取整;
是对
取绝对值运算;
是混沌序列
的第
个值到第
个值。
是对
进行靠近取整;
是对
取绝对值运算;
是混沌序列
的第
个值到第
个值。
Step 5:把
中的每一行二进制数分别进行扰乱,得到矩阵
,扰乱公式如下:
(7)
其中
是矩阵
的第
行的所有列,
是把行向量
的所有元素按顺时针方向移动
个单位;
Step 6:把矩阵
的第1列与第2列互换;第3列与第4列互换;第5列与第6列互换;第7列与第8列互换,得到矩阵
。
Step 7:把
转换成十进制数,再把已经转换成十进制数的
转换成1行
列的矩阵
;
Step 8:把
与
进行按位“异或”运算,得到一个新的序列 ,把
转换成
的矩阵
。
,把
转换成
的矩阵
。
Step 9:把
与
进行按位“异或”运算,得到一个新的序列
,把
转换成
的矩阵
。
Step 10:把
与
进行按位“异或”运算,得到一个新的序列
,把
转换成
的矩阵
。
Step 11:把
、
、
作如下处理,得到矩阵
,即最终的加密图像,
;
;
。 (8)
3.2. 解密算法的描述
Step 1:把矩阵
作如下处理,得到矩阵
、
、
,
;
;
。 (9)
Step 2:输入初始密钥
,迭代系统(2)
次,产生两条混沌序列
。
Step 3:把混沌序列
和
做如下处理:
(10)
(11)
(12)
(13)
Step 4:把
序列作如下处理:
(14)
Step 5:把
、
、
分别进行按位“异或”运算,得到序列
、
、
,再把序列
、
、
做如下处理,得到序列
,
(15)
Step 6:把
转换成二进制数,同时把已经转换成二进制数的
的列和行还原,得到矩阵
。
Step 7:把
转换成十进制数,并且转换成
的矩阵
。
Step 8:把
做如下处理,得到矩阵
,解密图像
,
;
;
。 (16)
4. 实验结果
4.1. 实验平台
PC机配置:Intel (R) Core (TM) i3-4170 CPU @ 3.70 GHz 3.70 GHz,内存4 GB,Windows7 32位操作系统。通过Matlab R2014a编写程序实现上述加密算法。
4.2. 实验结果
实验选取了经典的Lena,baboon,boat 3幅彩色图像,其大小均为256
256,对于其它大小的彩色图像也同样适用。明文图像,加密图像和解密图像如图3所示。
5. 安全性分析
5.1. 密钥空间分析
决定图像加密算法强度的最重要因素之一是密钥空间的大小。本文的初始密钥由
组成,以计算机精度为
计算的话,本算法的密钥空间大于
。如果一种图像加密算法的密钥空间大于
,则它就是安全的 [22] [23] 。因此本算法是足够安全的。本算法与其它算法的密钥空间比较结果如表1所示:

Figure 3. Plain text, encrypted image and decrypted image
图3. 明文图像,加密图像和解密图像

Table 1. Comparison of key space between this algorithm and other algorithms
表1. 本算法与其它算法的密钥空间比较结果
5.2. 直方图分析
直方图可以很好的反映图像像素值的分布情况,直方图越平坦则像素值分布就越均匀。图4是Lena的原图像R、G、B三个通道直方图和加密后图像R、G、B三个通道的直方图。
5.3. 信息熵分析
信息熵是最重要的随意因素之一。计算公式如下:
(17)
这里的
是
的机率,
是
的总数量。对于灰度图像来说,信息熵的最大值为8。Lena、baboon和boat的信息熵值如表2所示。

Figure 4. Lena’s original image R, G, B three-channel histogram and the encrypted image R, G, B three-channel histogram
图4. Lena的原图像R、G、B三个通道直方图和加密后图像R、G、B三个通道的直方图

Table 2. Entropy analysis table for plaintext and encrypted images
表2. 明文图像与加密图像的信息熵分析表
5.4. 不动点比和灰度平均变化值分析
不动点比为图像加密后灰度值未发生变化的像素点占所有像素点的百分比,计算公式如(18)所示;而灰度平均变化值能更好的评价加密图像灰度变化的程度,计算公式如(19)所示。
,其中
(18)
由公式(18)计算出本算法的不动点比如下表3所示:

Table 3. Fixed point ratio analysis of encrypted images
表3. 加密图像不动点比分析表
(19)
其中
为明文图像,
为密文图像。根据公式(19)计算出本算法的灰度平均变化值如下表4所示:

Table 4. Analysis of average change of grayscale
表4. 灰度平均变化值分析表
6. 结束语
本文提出了一种基于改进的Henon混沌映射与Bit位扰乱的彩色图像加密算法。首先,我们把明文图像的R、G、B三个通道合并成一个矩阵,同时还把其转换成二进制数;其次,把二进制数矩阵的行列进行扰乱,并把扰乱了的二进制数矩阵还原成十进制数矩阵;最后,把其分成三个像素个数相同的矩阵,再分别把三个矩阵进行按位“异或”运算,得到最终加密图像。实验结果和理论分析表明该算法具有密钥空间大,密钥敏感性高,能够有效地抵御统计分析和灰度值分析的攻击,对数字图像的加密具有良好的加密效果。
基金项目
湖北民族学院博士启动基金项目(MY2018B014)。
NOTES
*通讯作者。