1. 引言
水文现象属于综合性的自然现象,是一个由多种因素相互作用的复杂过程。水文尺度是指水文过程及其观测或模拟的特征时间或特征长度,一般包括空间尺度和时间尺度 [1] [2] 。不同水文尺度下水文过程表现出的规律和特征也不同 [1] 。作为描述各种尺度中水文特性及其变化的水文模型,它具有尺度特征和高度的时空变异特性 [3] 。在研究同一水文现象时,若采用的时间尺度或空间尺度大小不一致,得出的结论会有很大的差别。因此,研究不同时空尺度下水文模型参数敏感性程度具有理论和应用价值。
目前敏感性分析的方法主要分为两大类:局部敏感性分析和全局敏感性分析。局部敏感性分析易于操作,但只能评价单个参数对模型输出的影响,受“异参同效”现象影响较大;全局敏感性则考虑了参数的相互作用及共同响应,适用于复杂系统的研究分析 [4] [5] 。常用的全局分析法有多元回归法、RSM、LH-OAT、Sobol、Extend FAST、GLUE等方法 [6] 。罗智峰等 [7] 分析了DHSVM模型DEM在多尺度下的洪峰、洪量、地表、地下径流等水文要素和参数敏感性的响应,发现网格大小对水文过程影响很大,并且模型参数在不同尺度下的敏感性也不相同。常晓栋 [8] 等运用Sobol法分析不同量级洪水情景及不同预报精度评价标准下SWMM模型参数的敏感性,发现参数敏感性在不同情况下表现均不同,并且随洪水量级增加,参数相互作用逐渐减小。齐伟 [9] 等使用Sobol’方法对TOPMODEL模型单个参数和参数组合对洪水模拟指标影响进行了定量分析,发现参数单独作用的影响较小,土壤下渗指数衰减速率和下渗滞时组合对纳西效率系数、径流总量相对误差和洪峰相对误差影响显著。
本文以建溪流域及子流域为研究对象,对不同时间尺度(1 h,3 h、6 h、12 h和24 h)和空间尺度(按照河流等级由低到高依次选取武夷山站、建阳站和七里街站),先采用Monte Carlo法定性分析新安江模型的敏感参数,再利用Sobol敏感性分析法定量表述参数的敏感程度,并研究敏感度在不同时空尺度下的变化规律。
2. 研究区域和数据
建溪是闽江上游三大溪中最大的溪流,发源于武夷山的仙霞岭,由崇溪、南浦溪和松溪三大水源组成。位于北纬26˚31'~28˚31',东经117˚31'~119˚00'之间,河道全长635.6 km,整个流域面积为14,787 km2,约占闽江流域总面积的27%。该流域处于亚热带季风气候地区,空气湿润,降水充沛,年平均降雨量约为1800~2200 mm,年径流量为164亿m3,约占闽江总流量的1/3。
本研究收集了2000年至2013年1h时段的降雨、径流和蒸发资料,通过数据处理得到时间间隔3 h、6 h、12 h、24 h的数据。建溪流域的水文站点空间分布以及子流域分布如图1所示,全流域内共有8个水文站,16个雨量站及3个蒸发站。研究所选区的武夷山站、建阳站、七里街站分别位于上游二级支流、上游一级支流和干流。以上所有数据均来源于福建水口水库和福建省水文局的整编资料及水文年鉴,数据来源较为可靠,无明显质量问题。

Figure 1. Geographical distribution of hydrological stations and sub-basins in Jianxi basin
图1. 建溪流域水文站点及子流域的空间分布图
3. 新安江模型和敏感性分析方法
3.1. 新安江模型
赵人俊等 [10] 建立了一个降雨径流模型,即新安江模型,其特点是蓄满产流,认为在湿润地区只有当土壤含水量达到田间持水量时才产生径流。新安江模型广泛应用于国内外湿润半湿润地区,实际应用效果较好。
新安江模型的计算主要包括蒸散发计算、分水源计算、产流计算、汇流计算,共涉及到15个参数。可依据物理意义将这些参数划分成四类,各类别下的模型参数以及各参数的不同物理定义如表1所示。
3.2. SCE-UA算法
SCE-UA算法是美国亚利桑那州大学的段青云博士于1993年提出的一种全局优化算法 [11] 。它结合了随机搜索算法,确定性搜索算法,聚类分析及生物竞争演化等方法的优点,能够迅速高效地搜索到全局最优解,被广泛应用于水文模型中。本研究中将以均方误作为目标函数,采用SCE-UA全局优化算法进行参数率定。
3.3. Sobol敏感性分析方法
Sobol法于1993年被首次提出,是一种基于方差分解的全局敏感性定量分析方法。它的关键思想就是通过分解,将目标函数的总方差分解成单个参数的方差和参数间相互作用产生的方差 [12] 。Sobol能够精准地定量描述单个独立变量的敏感性以及参数之间相互作用带来的敏感性,其原则是当参数的一阶敏感度、总敏感度超过0.1即为敏感参数,并且数值越大越敏感 [13] 。近年来学者们广泛使用Sobol法,分析复杂水文模型中参数及参数间相互作用的敏感性问题,Tang等 [14] 综合比较了四种参数敏感性分析方法,发现Sobol方法有较强的稳定性和可实现性,能有效分析集总式水文模型的参数敏感性及参数之间相互作用。
以建溪流域及子流域为研究对象,横向采用不同时间尺度(1 h, 3 h, 6 h, 12 h, 24 h),纵向依据河流等级采用不同空间尺度(武夷山站、建阳站、七里街站),对新安江模参数敏感性进行分析比较。评价指标分别采用径流模拟过程的纳西效率系数(NSE)和水量相对误差(RE)。

Table 1. Classification of Xin’anjiang model parameters and its physical significance
表1. 新安江模型参数分类及其物理意义
4. 结果分析和讨论
4.1. 建溪及子流域降雨径流关系分析
对不同空间尺度的流域,根据实测资料挑选20场洪水,分别计算降雨量和径流深,绘制散点图并按照河流等级从低到高排列如图2所示。从图中可以看出,各子流域的降雨量与径流深均能较好地拟合成一条直线,随着降雨量的增大,径流深也在增加;并且河流等级越高,流域数据点与拟合直线的相关系数越高,因为除了降雨之外,其他因素(如土地利用、地形特征等)也对径流产生影响,而这种影响对小流域作用更为明显。
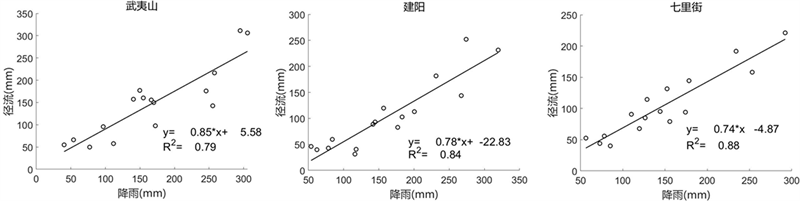
Figure 2. Variation of rainfall runoff relationship in different spatial scales
图2. 不同空间尺度降雨径流关系变化图
4.2. 建溪及子流域模型参数率定
将不同时间尺度下各子流域的水文资料代入新安江模型中,在同一参数可行域内(见表1)进行参数优选,采用纳西效率系数作为评价指标,结果如表2所示。由表可以看出,当时间尺度小于12h时,随着时间尺度的增大,模型的模拟精度逐渐提高;当时间尺度达到12 h后,模拟精度有较为明显的降低。这是因为当时间尺度达到12 h后,径流序列的长度显著缩短,并且在由短时间尺度向长时间尺度转换的过程中,径流序列携带的信息有所丢失,造成了模拟精度的下降。

Table 2. Parameter setting results in different spatial scales
表2. 不同空间尺度的参数率定结果
4.3. 不同时空尺度下新安江模型参数敏感性定性分析
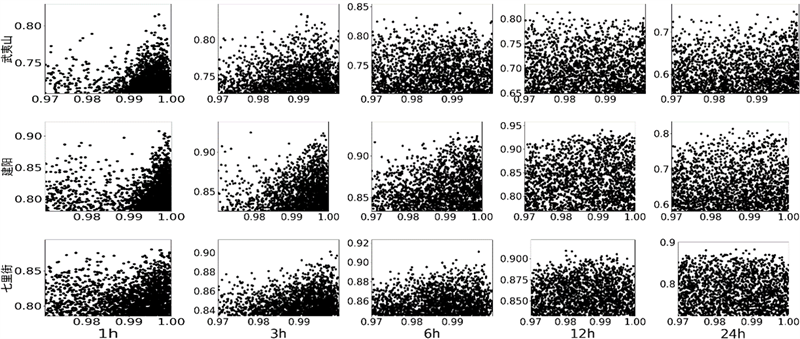
以建溪流域及子流域为研究对象,在不同时间尺度下,以纳西效率系数NSE为评价指标,采用Monte Carlo方法在可行域内随机生成参数组,对径流进行100,000次模拟。按照NSE从大到小的顺序排列参数组,选取前2000组参数进行分析。根据绘制所得参数似然散点图分析得到的敏感参数为KE、KI、CI、CG、N和NK,由于一些参数散点图较为相似,因此选取了各时空尺度下部分敏感参数的似然散点图如图3所示,其中横向表示时间尺度由小到大,纵向表示空间尺度由小到大。对于横向时间尺度而言,当时间尺度较小时,KE、KI、CI和CG在取值范围的一个小区间内高概率分布,随着时间尺度的增大,散点分布越来越均匀,说明参数在短时间尺度较为敏感,因为这些参数主要控制流域产流部分;而N、NK恰好相反,它们在长时间尺度下集中分布,表现出较强的敏感性,因为这两个参数反映了流域调蓄作用。对于纵向空间尺度而言,随着子流域面积增大,CI、NK分布变得集中,敏感度增强;N 的散点分布变得均匀,即在大空间尺度下敏感度降低。
4.4. 不同时空尺度下新安江模型参数敏感性定量分析
为了确认抽样样本数目是否满足敏感性指标达到收敛的条件,本文采用拉丁超立方抽样法,选取不同样本数量(500, 1000, 1500, 2000, 2500, 3000)进行敏感度计算。图4给出了时间尺度为1 h时在不同样本数目下各参数一阶敏感度和总敏感度的运算结果。从图4可以看出,当样本数目达到2500至3000时,各个参数的一阶敏感度和总敏感度基本上趋近于稳定,即可以认为敏感性指标达到了收敛,所以在该条件下计算所得的敏感性指标是较为可信的。
 (a)
(a)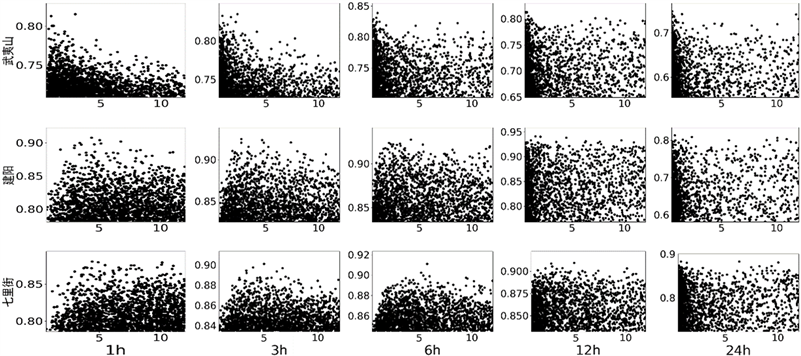 (b)
(b)
Figure 3. Scatter plot of the likelihood parameter sensitivity value of Xin’anjiang model
图3. 部分新安江模型敏感参数似然值散点图
因此每个参数抽取3000个样本,对各个子流域在不同时间尺度下参数敏感性进行比较与分析。根据计算的结果发现,对于相同的评价指标,不同子流域随时间尺度变化的敏感参数基本是一致的。图5表示评价指标不同时建溪流域不同时间尺度下参数的一阶敏感度和总敏感度,在图中敏感参数用色块标出,并且颜色越深越敏感。从图中可以看出,敏感性分析采用的评价指标不同时,得到的敏感参数也不同。当评价指标为NSE时,敏感参数为KE、SM、KI、KG、CI、CG、N和NK,这些参数分别属于蒸散发系数、分水源参数和汇流参数;因为纳西效率系数反映了实测流量过程和模拟流量过程的拟合情况并侧重洪峰部分,而蒸散发参数直接决定径流大小,分水源参数和汇流参数共同作用对流量过程线的形状产生影响,所以属于敏感参数。当评价指标为RE时,蒸散发折算系数KE的敏感度很高,WM和X也具有一定的敏感性,这几个参数属于蒸散发参数和产流参数;因为水量平衡误差侧重模型的产流部分,而蒸散发参数影响产流总量,产流参数影响径流模拟的产流过程,都很重要。

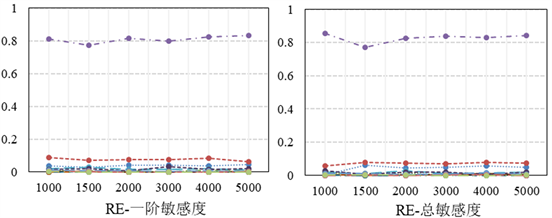
Figure 4. Sensitivity of each parameter with different sampling numbers when the time scale is 1 h
图4. 时间尺度为1 h不同抽样数目各参数一阶敏感度和总敏感度变化


Figure 5. Parameter sensitivity corresponding to time scales under different objective functions (The sensitivity threshold is 0.1, and the sensitive parameters are marked with color blocks, and the darker the color, the more sensitive the parameter is.)
图5. 不同目标函数下不同时间尺度对应的参数敏感度(敏感度阈值为0.1,敏感参数用色块标出,并且颜色越深越敏感)
以不同时间尺度为x轴,不同空间尺度为y轴,总敏感度为z轴点绘敏感参数在不同时空尺度下的敏感度,研究随时空尺度的变化规律。当评价指标为NSE时,随时空尺度改变规律变化的参数有KE、KI、KG、CI、CG和N,它们的敏感度如图6所示。由图可知,对于各子流域,随着时间尺度的增大,KE、KI、KG、CI的敏感度降低,N、CG的敏感度增强;并且子流域面积越小,CG随时间尺度的改变程度越大。短时间尺度下,产流过程对模拟结果的影响比较大,其中KE决定的蒸散发量直接影响产流的多少,KI、KG决定壤中流和地下径流的大小,CI影响壤中流的流消退过程,都对流量过程产生作用,因此敏感度较高;而随着时间尺度变大,汇流过程对径流模拟的影响增强;其中N反映流域的调蓄作用,决定流域的汇流时间;CG影响地下水的汇流过程,因此敏感度较高。
当评价指标为RE时,不同时空尺度下敏感参数的敏感度如图7所示。对于各子流域,随着时间尺度的增大,KE、WM和X的敏感度降低,CG的敏感度增强。并且子流域面积越小,时间尺度的改变对KE、CG敏感度的影响越强。由于KE控制总水量平衡,所以在各时间尺度下均保持较高的敏感度。短时间尺度下,地表径流对模拟结果的影响较大,而X和WM直接影响了上层土壤含水量,决定地表径流的大小,因此敏感度较高;随着时间尺度变大,地下水对径流模拟的影响增大,CG影响了地下水的消退过程,所以敏感度逐渐增强。同时当空间尺度变大,水文数据更加精确,在由短时间尺度向长时间尺度转换时保留的信息更多,径流模拟的精度改变较小,因此参数敏感度的改变程度较小。
如图8所示,当采用同一时间尺度时,不论评价指标是NSE还是RE,随着子流域面积的增大,CG的敏感度都在降低。CG与流域地下水汇流及消退过程相关,对流量过程线影响很大;当流域面积变大,调蓄能力增强,流量过程线形状变化相对平缓,因此CG敏感度变低。
5. 结论
本文以福建闽江建溪流域为研究对象,对其流域内各个水文站点所观测得到的2000年至2013年的降雨径流蒸发等水文数据进行整理,分析了流域降雨径流的关系。同时在不同时间尺度(1 h, 3 h, 6 h, 12 h, 24 h)下和空间尺度(不同等级河流的子流域)应用新安江模型进行径流模拟,采用SCE UA算法比较不同尺度下径流模拟的精度,同时分析了不同时空尺度下模型参数的敏感性,得出如下结论:
1) 随着时间步长的增大,新安江模型模拟精度先不断增高,但由于水文数据由短时间尺度转为长时间尺度时,部分水文信息丢失,在时间步长达到12 h后模拟精度开始降低。
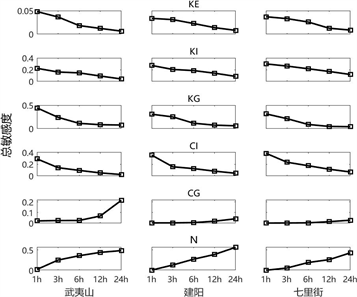
Figure 6. The variation of parameter sensitivity with different time scale when the index is NSE (The sensitivity threshold is 0.1)
图6. 评价指标为纳西效率系数时参数敏感性随时间尺度变化规律(敏感度阈值为0.1)
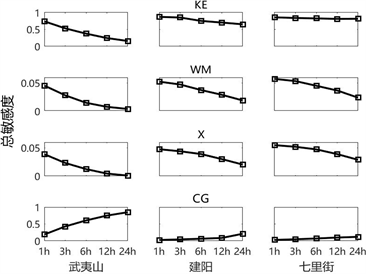
Figure 7. The variation of parameter sensitivity with different time scale when the index is RE (The sensitivity threshold is 0.1)
图7. 评价指标为水量平衡相对误差时参数敏感性随时间尺度变化规律(敏感度阈值为0.1)
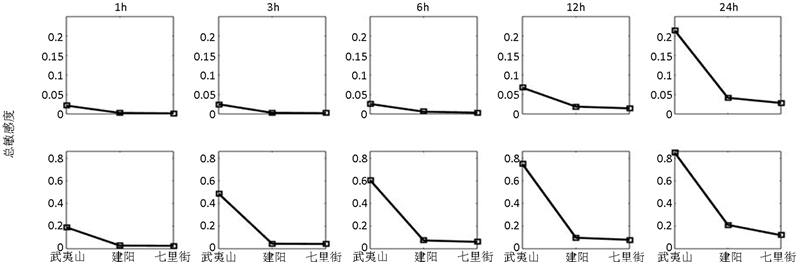
Figure 8. The sensitivity of CG changes with spatial scale (The sensitivity threshold is 0.1)
图8. CG敏感性随空间尺度变化规律(敏感度阈值为0.1)
2) Monte Carlo法定性分析得到的敏感参数为KE、KI、CI、CG、N和NK,Sobol法定量分析得到的敏感参数为KE、SM、KI、KG、CI、CG、N和NK,两种方法得到的敏感参数基本一致,都属于蒸散发参数、分水源参数和汇流参数。
3) 随着时间尺度的增大,KE、WM、X、KG和CI的敏感度降低,N和CG的敏感性增强;随着空间尺度的增大,CG敏感度降低,并且时间尺度的改变对KE和CG的敏感度影响减弱。
基金项目
国家自然科学基金重点项目(51539009)。