1. 引言
大地电磁测深(Magnetotelluric,简称MT)是以天然电磁场为场源来研究地球内部电性结构的一种重要的地球物理手段。当交变电磁场在地下介质中传播时,由于趋肤深度的作用,不同频率的信号具有不同的穿透深度,在地面上观测大地电磁场,它的频率域响应将反映着地下介质电性的垂向分布情况。因此,研究大地电磁的频率域响应,可以获得地下不同深度介质的电阻率信息 [1] 。然而,当近地表存在局部导电不均匀体时,在外电场的作用下,电流流过不均匀体时,不均匀体表面会产生积累电荷,由此产生一个与外电场成正比的附加电场,导致实测电场产生畸变,根据实测电磁场计算的视电阻率也随之产生畸变,该畸变为静态效应或静位移 [2] [3] [4] 。
大地电磁正演模拟的数值方法主要有3种:有限单元法 [5] [6] [7] 、有限差分法 [8] [9] [10] [11] 和积分方程法 [12] [13] ,前两者经常用于二维数值模拟,后者主要用在三维数值模拟。而有限差分法作为一种经典的数值模拟方法,依靠其相对简单的理论基础及简便的计算过程,在地球物理正演计算中应用非常广泛。但传统有限差分法的网格采用均匀剖分方式,必然存在着计算精度与计算速度的矛盾。若将传统的网格剖分方式应用到大地电磁正演过程中,对于衰减极快的高频电磁波,很容易造成采样的不足;而对于衰减极慢的低频电磁波,却会出现过采样的情况 [14] 。因此,本文选择非均匀网格有限差分法模拟大地电磁的静位移响应,详细推导了非均匀网格有限差分正演算法,并对浅地表不均匀体模型进行了试算分析。
2. 非均匀网格差分正演算法
2.1. 边值问题
在二维地下介质中,大地电磁场
、
满足的偏微分方程为 [15]
(1)
和
(2)
式(1)和式(2)可统一表示成
(3)
对于TE极化模式,有
,
,
(4)
而对于TM极化模式,有
,
,
(5)
为了求解大地电磁正演问题的亥姆霍兹方程,即式(3),我们还必须给出相应的边界条件,如图1所示。
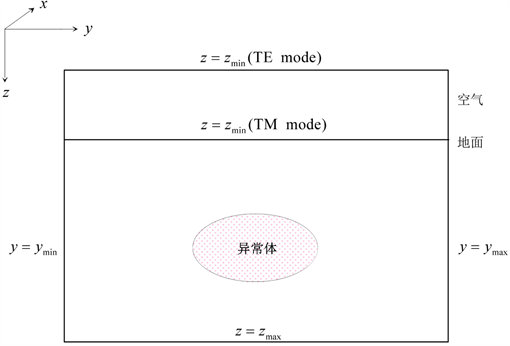
Figure 1. Boundary conditions of 2D geo-electric model
图1. 二维地电模型的边界示意图
1) TE极化模式的外边界条件
a) 上边界
离地面足够远,使异常场在边界上为零,即以该处的
为1单位
(6)
b) 下边界
为第三类边界条件,即
(7)
c) 取左右边界
、
离局部不均匀体足够远,电磁场在
、
上左右对称,其上的边界条件是
(8)
2) TM极化模式外边界条件
a) 上边界
直接取在地面上,并以该处的
为1单位,则有
2) 下边界
的边界条件,同TE极化模式,见式(7)。
3) 左右边界
和
的边界条件,同TE极化模式,见式(8)。
2.2. 差分线性方程组导出
将二维地电模型离散化,如图2所示。下面以求解TM极化模式的电磁场为例,详细推导差分正演算法。
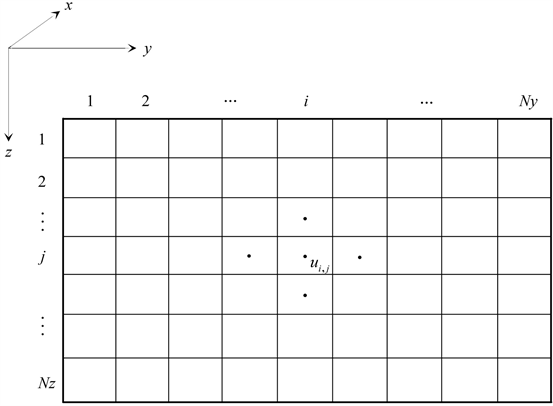
Figure 2. Discretization of 2D geo-electric model
图2. 二维地电模型离散化
对于研究区域的内部节点,在单元
中心处,采用有限差分近似计算偏导数:
(9)
和
(10)
将式(9)和式(10)代入到式(3),可得
即
(11)
或写成
(12)
令
(13)
推广到所有节点,将磁场所满足的4个边界条件待入,可得
(14)
这时,方程组含有
个方程以及
个未知数,该线性方程组的系数矩阵同样具有稀疏形式,如图3所示。求解上述线性方程组(14)即可得到各单元中心处的磁场值,从而可以进一步计算模型响应的视电阻率和相位。
2.3. 电磁响应计算
当计算出各单元中心的
值后,再利用数值方法求出场值沿垂向的偏导数
,它相当于
或
,代入到以下两式便可计算视电阻率和阻抗相位。
对于TE极化模式,有
(15)
对于TM极化模式,有
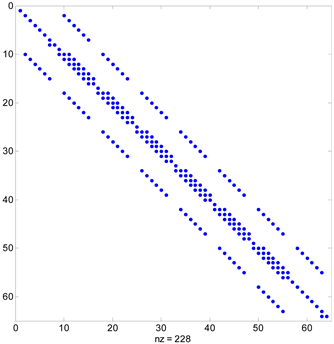
Figure 3. The coefficient matrix of finite difference method for 2D magnetotelluric responses
图3. 差分法计算二维大地电磁响应形成的系数矩阵
(16)
3. 静位移模型试算分析
选取的静位移模型为层状介质存在局部电性不均匀体,如图4所示。层状介质为三层A型地电模型,其模型参数为
,
,
,
和
;局部不均匀体的长和宽均为50 m,其电阻率值分别设置为
、
和
。
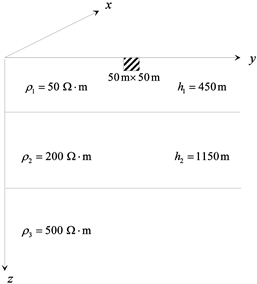
Figure 4. 2D geo-electric model with static-shift
图4. 二维静位移地电模型
利用有限差分法模拟静位移模型,我们设置的二维正演网格剖分为
,并选用40个记录频点(0.001~1000 Hz),计算的TM视电阻率腻断面如图5所示。从模拟结果可以看出,近地表存在局部电性不均匀体时,视电阻率值受静态效应的影响严重。当近地表不均匀体为低阻时,其所在位置下方各频点视电阻率较正常值偏低,拟断面表现为下凹;当近地表不均匀体为高阻时,其所在位置下方各频点视电阻率较正常值偏高,拟断面表现为上凸。
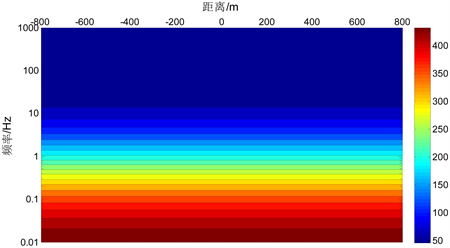 (a)
(a)
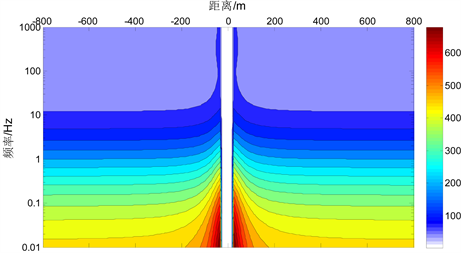 (b)
(b)
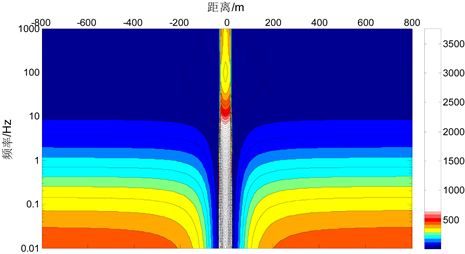 (c)
(c)
Figure 5. Pseudo-section map of magnetotelluric responses of the uniform body in TM mode
图5. TM极化模式下高阻与低阻局部不均匀体的大地电磁响应拟断面图
为了分析局部电性不均匀体对同一测点各频点的影响情况,我们选择不均匀体上方的中心点为研究对象。图6给出了局部低阻不均匀体与局部高阻不均匀体的视电阻率响应对比,从图上可以看出:当存在局部高阻不均匀体时,视电阻率—频率曲线整体上移,电磁感应效应可以忽略不计;当存在局部低阻不均匀体时,视电阻率—频率曲线整体下移,但高频段视电阻率曲线的趋势发生了变化,这是由于低阻不均匀体的电磁感应引起的。
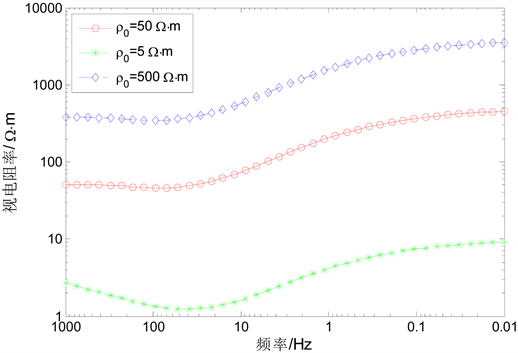
Figure 6. The resistivity-frequency curves of the uniform body in TM mode
图6. TM极化模式下高阻与低阻局部不均匀的视电阻率–频率曲线
4. 结语
1) 针对各向同性介质中大地电磁场所满足的边值问题,详细推导了二维地电模型大地电磁场响应的有限差分正演算法;在保证计算精度的条件下,本文的非均匀网格剖分方式能减少正演计算时间,提高计算效率。
2) 通过对浅部不均匀体模型的模拟计算,得到了大地电磁的静位移响应规律,同时也验证了非均匀网格有限差分正演算法的准确性。
3) 高阻不均匀体使受影响测点的视电阻率整体向上移动而趋势不变,并且不均匀体电阻率越高,视电阻率向上平移的幅度越大。
4) 低阻不均匀体使受影响测点的视电阻率整体向下移动,并且由于电磁感应现象,单点视电阻率曲线在高频段趋势发生变化。
基金项目
水能资源利用关键技术湖南省省重点实验室开放研究基金(PKLHD201702)资助。
NOTES
*通讯作者。