1. 引言
速度分析是地震资料处理中的关键环节 [1] [2] ,速度参数不仅关系到地震资料处理中诸多环节的质量,其本身也提供了关于地下构造和岩性的重要信息。因此,获取准确可靠的速度参数是地震资料处理的中心问题。
目前,我国页岩气资源调查与勘探开发还处于探索起步阶段,至今尚未对其潜力进行全面估算,页岩气资源有利目标区有待进一步落实,勘探开发还处于“空白”状态。为此,中石化在下扬子区页岩气 [3] 评价有利目标I类区,即XC探区部署了二维地震。其主要勘探目的是落实寒武系(中深层)页岩空间展布特征,确保获得寒武系及以上地层的反射波组,且能够分辨大于50 m的厚页岩层。从已获得的资料来看,页岩层埋深较深,波场复杂,且该区地表起伏剧烈,地震资料信噪比低。因此,地震资料处理中对速度拾取的精准度要求较高,否则会影响叠加、成像的精度。
速度分析的方法有很多,国内外很多学者对此进行了广泛而深入的研究。1969年Turhan和Koehler [4] 首先提出了将基于相似系数的相干准则运用到速度分析中;之后,De Vries和Berkhout [5] 提出了一种基于最小熵的速度分析方法,对绕射能量较强的反射波地震数据可以进行准确的速度拾取;Biondi和Kostov [6] 提出了基于特征值运算的速度分析方法;Simon [7] 提出了一种渐进的线性速度分析方法;吴树初和罗国安 [8] 提出了计算复数道相关速度谱的方法,可以增强相位的一致性;林小竹 [9] 提出的利用协方差算法求取速度谱,不但能提高速度谱的分辨率,还可以减少速度分析的计算量;另外,还有其他学者 [10] - [15] 研究了VTI介质下的速度分析方法以及层速度反演的相关算法等。1996年Morozov和Smisthson [16] 提出了基于相位相关速度分析方法,该方法利用统计假设检验方法计算速度谱,可以有效提高速度谱的分辨率;后来王德利及何樵登等 [17] 对该方法进行过研究,并取得了较好的效果;张军华等 [18] 进一步发展了相位相关速度分析方法,充分说明了该方法的优势。
2. 速度分析基本原理
常用求取叠加速度的方法有2种:速度扫描和速度谱。一般来说,速度扫描法的工作量大且繁琐,而速度谱的求取方法相对更易实现,在速度分析中应用速度谱求取叠加速度的方法更为广泛,同时也对各波组的识别提出了更高的要求。该次研究主要对叠加能量法和统计相位相关法两种方法进行了对比。
2.1. 叠加能量法
叠加能量法是常用的常规速度分析法。固定零偏移距时间d0进行速度扫描,当扫描速度等于均方根速度时,地震记录的反射信号相位相同,对应最大叠加能量的速度就是要提取的速度。进行速度分析所用的判别准则为平均振幅准则,当平均振幅A能够获得最大值时所对应的速度即为叠加速度。
平均振幅A可以定义为:
(1)
其中,M = T/Δt。
式中:N为地震记录的总道数,个;M为总采样点数,个;T是总采样时间,ms;Δt是采样间隔,ms;r表示与动校正存在一定关系的延迟量,1;ri为第i道的延迟量,1;fi,j为第i道、第j个采样点的反射波振幅,dB;
为第i道、延迟后的第j个采样点的反射波振幅,dB。
2.2. 统计相位相关法
实践证明叠加能量法的抗噪性能较差 [18] ,在页岩气复杂构造区,采用叠加能量法很难提供准确的速度。该次研究利用瞬时相位的相关特性,采用统计相位相关法计算速度谱 [17] 。根据统计假设检验原理,建立2个检验假设(设为R和W),再根据常规叠加能量的瞬时信息和能量函数计算速度谱。逐点计算速度谱,可以避免与时窗有关的时间分辨率损失,在提高时间分辨率方面明显优于叠加能量速度分析法。算法如下:
1) 设输入的道集为uij,表示第i道、第j个采样点。设初始时间为t0,选定其对应的速度v进行动校正,此时可以得到校正后的道集,再应用Hilbert变换法求取uij的瞬时振幅Aij和瞬时相位μij。
2) 将整个道集分为若干部分,即样点分布分为c组,样点的相位表示为
,且
,求取统计量R和W:
(2)
(3)
其中,
。
R假设检验与W假设检验是判断t0及所选定的v正确与否的标准。当R检验假设概率分布是单峰分布时,代表t0及所选定的v正确;当W检验假设概率分布在不同偏移距范围内,且都是相同的单峰分布时,代表t0及所选定的v正确。
3) 计算常规叠加能量的瞬时信息SB(t, v):
(4)
式中:uij(t, v)为动校正后信号的振幅,dB;t为第i道、第j个采样点道集对应的采样时间,ms;v为第i道、第j个采样点道集对应的速度,m/s;B是瞬时振幅算子,1;L是低通滤波因子,1。
4) 计算能量函数SRWB:
(5)
最后,根据第3)步和第4)步求得的值,计算速度谱。
3. 应用实例效果分析
影响速度分析精度的因素很多 [19] [20] [21] [22] [23] ,如叠加次数、排列长度、信噪比和静校正等。XC页岩气探区地震资料信噪比低、近地表异常都会对速度谱质量有影响,导致速度谱的分辨率过低,难以识别有效波组的能量团。为此,笔者进行了深入研究和分析,并提出了针对性的处理技术和方法。
3.1. 速度分析的预处理
3.1.1. 提高信噪比处理
信噪比低会降低速度谱的分辨率,不利于速度拾取,限制速度分析的精度。因此,为确保速度分析精度,需要进行地震资料的净化处理。
针对面波、异常振幅、线性进行多域、多方法组合进行压制,有效提高了地震资料信噪比,保护了目的层系的反射波组,最大限度地保留了有效波,确保无过度去噪现象。图1是XC页岩气探区某单炮去噪前、后对比图,可以看出,噪音得到了很好的压制,有效波同相轴清晰可见,反射层有效信息凸显出来,信噪比明显提高。图2为去噪前、后的叠加剖面对比图,可以看出,通过地震资料净化处理后,剖面同相轴连续性加强,信噪比显著改善。

Figure 1. The single shot result before (a) and after (b) denoising
图1. 去噪前(a)、后(b)单炮记录

Figure 2. The profile correlation before (a) and after (b) denoising
图2. 去噪前(a)、后(b)剖面对比图
3.1.2. 剩余静校正处理
高频静校正量的存在可以导致CMP道集同相轴的扭曲,相关特性变差,影响计算能量函数,从而影响速度分析精度,导致求取的速度不准确。
高频静校正量的求取一般依赖多种剩余静校正方法联合解决。XC页岩气探区地震地质条件非常复杂,炮检点布设困难,一定程度上存在炮检点位移现象,且地下介质非均质性强,地震波传播路径复杂。而地表一致性剩余静校正假设地层为水平层状介质,不能满足实际处理的需要。所以实际资料处理中,在采用地表一致性剩余静校正的基础上,通过外部模型控制进行非地表一致性剩余静校处理,最大程度地减少了高频静校正问题的存在,进一步消除了同一CMP道集内各道的残余时差,改善了地震资料的品质。
图3为剩余静校正前、后剖面对比图,可以看出,经过剩余静校正后,叠加剖面上的反射波组更加清晰、连续,同时信噪比得到了很大提高。
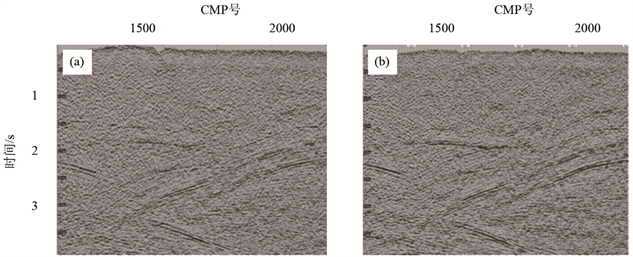
Figure 3. The profile correlation before (a) and after (b) residual static calibration
图3. 剩余静校正(a)、后(b)剖面对比图
3.2. 统计相位相关法速度谱的求取
在做好常规处理的基础上,采用上述两种方法进行速度谱求取。通过叠加能量法与统计相位相关法速度谱的对比分析(图4)可知,在统计相位相关法计算的速度谱中,深层的速度能量聚焦性好,能量团更集中,速度趋势走向合理,速度易于确定,明显优于叠加能量法。
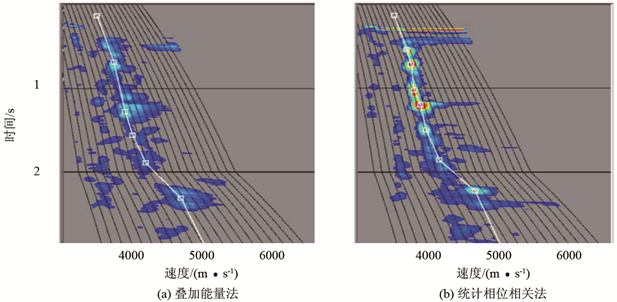
Figure 4. The velocity spectrums of different velocity analysis methods
图4. 不同速度分析方法的速度谱
图5是采用叠加能量法和统计相位相关法的叠加剖面对比图,通过对比可以看出,采用统计相位相关法的叠加剖面上,仍保持了相同的浅层地质特征,而中深层的构造成像质量明显改善,同相轴连续性增强,波组特征清楚,层间信息丰富。

Figure 5. The stack profiles of different velocity analysis methods
图5. 不同速度分析方法的叠加剖面
4. 结语
通过对速度分析方法的研究分析,在近地表高差大、岩性差异大、页岩层埋深大、波场复杂的区域,统计相位相关法计算速度谱的效果较好。该方法利用相位信息,不但可以识别较弱波组,且计算过程中不受边界效应影响,纵向的时间分辨率和横向的速度分辨率均较高,抗噪性强,速度谱能量团易于区分,明显优于叠加能量法。应用统计相位相关法的最终成像效果好,中深层的波组成像质量得到了明显提高,满足了复杂波场页岩气探区的勘探要求,为类似探区勘探提供了借鉴。