1. 引言
近年来,由于非线性科学技术的快速发展,神经元系统的复杂动力学行为备受关注。神经元是神经系统的基本组成单位,此外神经元也是大脑处理信息的基本单位。它由细胞体、树突、轴突组成,而信息的处理和传递主要发生在突触的附近,从而就存在时间延迟。在神经系统中,时滞在信息传递过程中都是不可避免和不可忽视的。目前,时滞系统的研究在部分领域已经取得了成就,例如,Wang [1] 等通过在HR模型的膜电势中加入时滞反馈项进而用泛函微分方程理论研究了含有时滞反馈的HR神经模型的混沌控制行为;Cheng [2] 等人进行了具有时滞的神经网络的分岔分析。为了揭示神经元复杂的动力学行为,人们建立了许多不同的神经元数学模型,如Hodgkin-Huxley (H-H)系统、FitzHugh-Nagumo (FHN)系统、Hindmarsh-Rose (HR)神经元系统等。其中,HR神经元具有简单的数学表达式,学多人对其耦合系统已经进行了研究。例如,曹淑红 [3] 等人研究了时滞对耦合神经元同步后放电模式的影响,结果表明时滞使得神经元的放电模式发生改变,同时时滞的增加能够诱导簇中的峰逐渐地减少或消失。
四变量Hodgkin-Huxley (HH)神经元模型 [4] 可以再现枪乌贼轴突的电活动特性,并可以估计离子通道嵌入膜中的随机效应。为了进行有效的动力学分析,通过简化原始HH神经元模型,建立了三变量Hindmarsh-Rose (HR)神经元模型 [5] 。HR神经元模型的动力学方程描述如下:
(1)
其中变量
分别表示膜电位、恢复变量的慢电流和自适应电流。该模型通过改变外加刺激电流可以产生静止态、尖峰放电、簇放电甚至混沌状态。此外,峰峰间隔(ISI)分岔分析使我们更好的理解了神经元的电活动 [6] [7] [8] 以及电活动模式之间的转换,甚至也同样有效于分数阶动力学系统 [9] 。大量研究证实分数阶Morris-Lecar神经元模型通过分岔分析可以呈现出丰富的簇放电模式和动力学行为 [10] 。对于HR模型中的分岔分析,可以参考文献 [11] 。进一步的,提出了一个具有四个变量和13个参数的改进的HR神经元模型(eHR神经元模型),以产生更复杂的动力学行为,其微分方程表达式为:
(2)
其中
是系统的参数,变量
分别表示膜电位、恢复变量的慢电流、自适应电流和一个缓慢的动态过程量。在本文中,选取此神经元模型作为研究目标,引入一个时滞作用于慢变量上,考虑时滞对快慢系统的动力学行为的影响。
2. 模型介绍
引入时滞的eHR神经元模型具体形式如下:
(3)
其中
表示时滞,其他参数与模型(2)参数意义相同。且带时滞的系统也可以看做自反馈系统。
3. 平衡点分析和Hopf分岔存在性稳定性分析
假设系统的非平凡平衡点为
,通过代换
,
,
,
,将系统平衡点移至原点,并将
,
,
,
记为
,
,
,
,则系统(3)可重新改写为如下系统:
(4)
系统(4)在原点的线性化系统为
(5)
系统(5)对应的雅克比矩阵为:
其对应的特征方程为:
(6)
其中
根据系统中时滞
的值,分以下几种情形讨论:
情形1:时滞
时,特征方程(6)变为
(7)
其中
。
根据Routh-Hurwitz准则,得到如下结论:
当特征方程所对应的系数值满足如下条件
(H1)
。
则方程(7)的全部根满足具有负实部的条件,那么,系统(4)在平衡点处是渐进稳定的,即系统(3)在平衡点处是渐进稳定的。
情形1:时滞
时,考虑特征方程(6)
令
是方程(6)的根,则有
(8)
分离方程(8)的实部和虚部可得:
那么
(9)
其中
把上述方程各式平方可得:
(10)
其中
令
,则方程(10)变为:
(11)
令
不失一般性,假设方程(11)有四个正根,分别记为
。因此,方程(10)有四个正根
。
由方程(9),记
令
是特征方程(6)在时滞
附近满足
,
的根,可以得到如下横截性条件。
设
且
,则
且
与
有相同的符号。
则可得如下结论:
引理1:i)当
,方程(6)的所有根具有负实部,系统(1)的平衡点
是渐进稳定的;当
,平衡点
是不稳定的。
ii) 若
,在临界值
时,系统(3)在平衡点
处发生Hopf分岔,即一组非常数周期解会从平衡点分岔出来。
4. Hopf分岔的方向及稳定性
通过分析可得对于每个
系统(3)会发生Hopf分岔。本节利用中心流行定理和稳定性理论,判定了分岔周期解的稳定性和分岔方向。
假设
,
。令
,
,并将系统(3)在定义域
上转化为微分方程。
定义线性算子
和非线性算子
,其中
,
其中
,式中
。
由Riesz表示定理,对于
,存在一
的有界变量的矩阵函数
,使得
实际上,可取
对于
,定义
和
。
则系统(3)等价为
对于
定义
和一双线性内积
假设
对应特征值为
,则
也是
的特征值。令
是
对应特征值
的特征向量,
是
对应特征值
的特征向量,则有
,
。这就保证了
,
。
下一步,使用Hassard等人的判断记号,计算中心流形
在
处的坐标。
其中
因此可以计算下面数值:
综上,可得下面有关Hopf分岔方向及周期解稳定性的结论:
当
时,分岔周期解存在(不存在);若
,周期解的周期增加(减小);
,在此中心流形上,周期解是渐进稳定的(不稳定的)。
5. 数值模拟
在本节我们给出部分数值模拟来验证以上结论,其中参数的值为
,
,
,
,
,
,
,
,
,
,
,
,
。此时,系统变为
(2)
通过计算可得系统的唯一平衡点为P (0.881210, 2.781651, 2.870551, 3.643691),由此可得
显然满足条件(H1),在初值(0.3, 0.3, 3.0, 0.05)处平衡点P (0.881210, 2.781651, 2.870551, 3.643691)是渐进稳定的,如图1所示。
当
时,由情况2的理论方法计算得
,由引理1可得满足横截性条件。当
时,系统是不稳定的,当
穿过每一个临界值
是,系统(3)的一个稳定周期
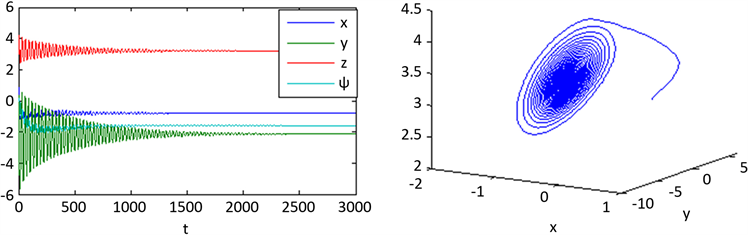
Figure 1. τ = 0, The time serise and phase diagrams of x(t), y(t), z(t), w(t) at the initial values (0.3, 0.3, 3.0, 0.05) show that the equilibrium point P (0.881210, 2.781651, 2.870551, 3.643691) are asymptotically stable
图1. τ = 0时,在初值(0.3, 0.3, 3.0, 0.05)处x(t),y(t),z(t),w(t)的时间响应图和相图,平衡点P (0.881210, 2.781651, 2.870551, 3.643691)是渐进稳定的
解从P (0.881210, 2.781651, 2.870551, 3.643691)分岔出来,产生Hopf分岔。如图2所示;当
时,系统(3)在平衡点P (0.881210, 2.781651, 2.870551, 3.643691)处是渐进稳定的,如图3所示。

Figure 2.
,The time serise and phase diagrams of
at the initial values (0.3, 0.3, 3.1, 0.1) show that The unique equilibrium point P (0.881210, 2.781651, 2.870551, 3.643691) is unstable and a stable periodic solution bifurcates from P
图2.
时,在初值(0.3, 0.3, 3.1, 0.1)处
的时间响应图和相图,唯一平衡点P (0.881210, 2.781651, 2.870551, 3.643691)是不稳定的且一个稳定的周期解从P分岔出来
6. 结束语
目前,大多人研究了具有时滞的耦合神经元系统,对单个神经元引入时滞项的研究较少。而时间延
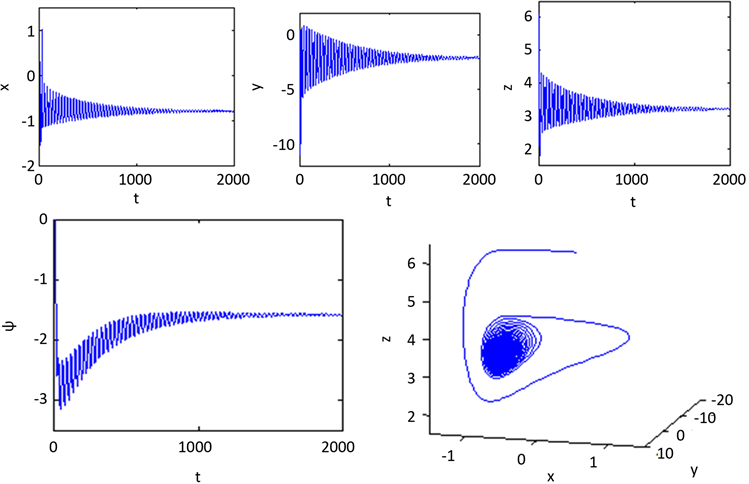
Figure 3.
, The time serise and phase diagrams of
at the initial values (0.3, 0.3, 6.1, 0.1) show that the equilibrium point P (0.881210, 2.781651, 2.870551, 3.643691) are asymptotically stable
图3.
时,在初值(0.3, 0.3, 6.1, 0.1)处
的时间响应图和相图,平衡点P (0.881210, 2.781651, 2.870551, 3.643691)是渐进稳定的
迟真实的存在于信号的传播过程中,且时滞的出现使得神经元系统发生更为复杂的动力学行为,因此对时滞神经元系统的研究具有重要的实际意义。本文通过对eHR神经元模型引入时滞项,给出了平衡点的稳定性和发生Hopf的条件,推导出了时滞
发生Hopf分岔的临界值
。另一方面,为验证所得结论进行了数值模拟,通过时间响应图和相图更好的验证了Hopf分岔方向及分岔周期解的稳定性。