1. 前言
在统计学中,经常会遇到高维积分的计算问题,而使用传统的数值方法往往很难解决实际问题。随着计算技术的提高,随机模拟的方法为解决这些高维积分问题提供了一个很好的思路。
马尔可夫链蒙特卡罗(Markov Chain Monte Carlo, MCMC)方法的理论框架来源于Metropolis (1953)和Hasting (1970) [1] ,首先在
的状态空间中模拟出一条马尔可夫链,使得该马尔可夫链的稳定分布就是目标分布
。此时在这个状态空间游走时,每一个状态
停留的时间正比于目标分布
。为了有效的得到目标分布,此时引入一个容易抽样的建议概率密度函数
,在每一次的抽样过程中,先从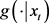 抽样得到一个候选样本
,接着再按照后面提到的原则决定是否接受该样本。显然这样产生的随机序列是一个离散时间的时齐的不可约遍历Markov链。
抽样得到一个候选样本
,接着再按照后面提到的原则决定是否接受该样本。显然这样产生的随机序列是一个离散时间的时齐的不可约遍历Markov链。
这一算法已经在诸多领域进行推广以及改进,例如:应用统计学、金融学、计量经济学、计算物理学等领域。
在过去的几十年里,MCMC方法将复杂的多元问题简单化已经引起了许多人的注意。首先,在1953年,Metropolis,Rosenbluth,Teller [2] 在“MANIAC”计算机上实现物质状态方程的蒙特卡罗方法模拟,1970年Hasting [1] 将建议概率分布从对称分布变为非对称形式,这个算法称为Metropolis-Hasting (M-H)算法,也称为通用Metropolis算法。接下来就是Tanner、Rubinstein [3] 、Wong (1987)、Gelfand和Smith (1990)在细节处进行了优化。S.Chib和E.Greenberg (1995) [4] 对M-H算法的理解以及L.Tierney (1994) [5] 马尔可夫链在后验分布中的应用。在1984年Gelman提出了在研究图像恢复问题时提出了Gibbs算法。Liu (1996)提出了混合Gibbs算法以及Swendsen、Wang (1987)在原来的基础上发生了演变,形成了聚类算法。2003年C.Andrieu [6] 将MCMC算法应用于了机器语言,2011年,S.Brooks [7] 对MCMC的算法理论原理做出了更为细致的解读。
1.1. 马尔可夫链的基本概念
马尔可夫链理论是研究马尔可夫链蒙特卡罗方法的基础,为此先给出马尔可夫链的定义及基本性质。
1.1.1. 马尔可夫链的定义
如果对于任意时刻t,条件概率满足
则称此性质为马尔可夫性,若右式与t无关,则称X为时齐的。
引入记号:
为过程从状态x转移到状态y的概率,称为一步转移概率;
为过程从状态x经过n步转移后到达状态y的概率,称为n步转移概率。
给定状态序列
,状态空间S,为了简便书写,记
,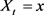 ,则转移概率为
,转移概率
组成的矩阵
,则转移概率为
,转移概率
组成的矩阵
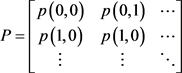
其中, p (x, y) ≥ 0 (x, y∈S ) ,
,称此矩阵为一步转移概率矩阵。
文中讨论的马尔可夫链都是时齐的有限马尔可夫链。
令
,则
是一个停时,称之为状态y的首中时,记
1.1.2. 马尔可夫链的性质
1) 常返性。如果从状态x出发以概率1回到状态x,即 ,称状态x是常返的,否则称状态x时暂留的。如果一个马尔可夫链所有状态都是常返的,则称这个马尔可夫链是常返的。记
为
,称状态x是常返的,否则称状态x时暂留的。如果一个马尔可夫链所有状态都是常返的,则称这个马尔可夫链是常返的。记
为
y的平均返回时间,如果平均回返时间
,其中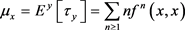 。
。
则状态x是正回返状态,如果平均回返时间
,则状态x是零回返状态。
若所有状态是暂留的,则称这个马尔可夫链是暂留的。状态x是常返的等价于
也等价于
。状态x是暂留的等价于
也等价于
。
如果
是互达的,则有
都是常返的,
且
;否则
都是暂留的,即
且
。
2) 不可约性。如果所有状态都存在n,使得n步转移概率
,等价于每一个状态都可以经过有限步到达其他状态,也就是每个状态都是联通的,称这样的状态为不可约状态。有限状态的马尔可夫链是不可约的,则这个马尔可夫链是正回返的。
3) 周期性。n步转移概率
,状态x的周期数为
。
上式中GCD{·}表示满足条件 {·} 且
的n的集合的最大公约数。若状态x的周期数
,则称状态 是非周期状态;若状态x的周期数
,则称状态 是周期状态。
4) 遍历性。如果状态i是正常返、不可约、非周期的,则称该状态i是遍历的。所有状态都是遍历的马尔可夫链,称为遍历的马尔可夫链。
5) 平稳分布。E上一个概率分布
,如果满足
,即
,则称
为转移矩阵Ρ的平稳分布,显然有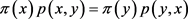 ,也就是π是可逆的。
,也就是π是可逆的。
1.2. 马尔可夫链蒙特卡罗方法原理
蒙特卡罗方法是一种随机模拟的方法,也就是求解随机事件发生的概率或者随机变量的期望时,通过设计一种抽样方法,得到某一个特定事件发生的频率,然后使用这个频率来表示相应事件发生的概率。但是随着维数的增加,采样所需的样本量(或者说接受的概率)随维数增加而指数增长,导致计算量太大,速度太慢,为了克服这一问题,也就应运而生了马尔可夫链蒙特卡罗(MCMC)方法。MCMC算法通过构造Markov链的极限平稳分布来模拟计算积分,转化成从已知概率分布抽样,也就是先选择一个建议概率分布,从建议概率分布抽样产生一个候选样本值,则可以建立可操作的状态转移规则,用接受概率判断状态是否转移,重复这个过程,将产生一条马尔可夫链。其中,Markov链满足大数定律:
假设
为一平稳分布π的遍历的Markov链,则
依概率收敛到分布为π的随机变量X,且对任意函数g,满足
存在,当
时,有
。
如果生成的马尔可夫链是遍历的,也就是它满足正常返性、不可约性和非周期性,经过足够多的状态转移后,马尔可夫链的转移概率会趋于一个平稳分布,即事先给定的目标分布,马尔可夫链的各个状态就是随机变量的样本值,这样也就实现目标分布的随机抽样。
2. Metropolis-Hasting(M-H)算法及推广
Metropolis算法是MCMC的核心,其实也就是改进的接受-拒绝抽样方法。接受-拒绝算法的具体步骤如下:
1) 首先选择一个容易抽样的分布作为建议概率分布,记为
,接着确定一个常数C,其中
,使得在x的定义域上都有
。
2) 生成服从建议概率密度函数的
的随机数y。
3) 接着生成一个服从均匀分布
的随机数u。
4) 计算接受概率
,如果
,则接受y,否则继续转到第(2)步。
5) 不断重复(2)~(4)就可以生成一组服从目标分布 f ( x) 的随机数序列。
类似于拒绝–接受抽样方法,在当前状态
下产生下一个状态只需在原来拒绝–接受抽样方法下作一点改变得到Metropolis算法 [8] ,具体如下:
1) 首先构造建议概率分布
,并从建议概率分布
,其中
,产生一个随机数y作为下一个状态。
2) 接着按从均匀分布
的随机数u,如果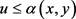 ,则接受该建议的随机数 ,即
,否则
。
,则接受该建议的随机数 ,即
,否则
。
3) 重复上述过程,我们就可以得到一组仅依赖于上一个随机数并且与前面随机数无关的随机序列。
4) 计算接受概率
。
显然在这里,建议概率密度函数
的作用主要是转移当前的状态,也就是为每一个状态构造出一个邻域,并且下一个状态就是这个邻域中的某一个数。
Metropolis算法的应用受到了建议概率分布的对称形式的限制,因此,Hasting把建议概率分布从对称分布形式推广到一般情况,形成了Hasting算法,也称之为通用梅特罗波利斯算法,此时接受概率变为
。
接受概率的选择过程S. Chib和E. Greenberg (1995) [4] 做了详细的解说。
2.1. 收敛性证明
要Metropolis算法收敛也就是证明马尔可夫链收敛到平稳分布,即证明这里的马尔可夫链具有下列三个性质。
1)
不可约和非周期,则
也不可约且非周期的。
2)
可逆且满足细致平衡条件。
3) 满足不变性。
满足不变性。
Proof. 1) 由马尔可夫链性质知,当马尔可夫链满足不可约性和非周期性,那么m步转移概率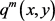 产生的任何m步跟踪路径为大于零的一个值,由于m步转移函数
具有正概率,所以
也不可约且非周期的。
产生的任何m步跟踪路径为大于零的一个值,由于m步转移函数
具有正概率,所以
也不可约且非周期的。
2) 因为
所以
,即
满足细致平衡条件,则
可逆。
3) 根据马尔可夫链的性质知,满足细致平衡性也就确保了不变性,所以就可以达到整个马尔可夫链总体的平衡 [9] 。下面要证明马尔可夫链满足不变性也就是满足
在离散和连续的情况下,有
同理,
所以对于不可约的概率分布
,不论这个初始分布怎样变化,它最终都会趋于平稳分布
,于是有,
。
由上可知,马尔可夫链满足不变性。
2.2. 例子
建议概率密度为支撑集
[10] 上的建议概率分布
,从密度函数
进行采样,此时接受概率
。接受概率随样本变化以及随x的变化见图1和图2。
由图1和图2可知,随着样本数的增加,接受概率的变化逐渐趋于稳定,此时在x在区间
接受概率最高。同时算法的收敛性也验证了样本遵从已知概率分布,也就是,找到了合适的马尔可夫链,使得这个马尔可夫链的稳定分布也就是目标分布,并且,每一个状态的停留时间也正比于目标概率(程序见附录A)。
3. 建议概率分布改进
由于上述的Metropolis-Hasting (M-H)算法存在收敛速度慢、接受概率低、抽样效率不高、样本呈现

Figure 1. Acceptance probability varies with sample size
图1. 接受概率随样本数变化

Figure 2. Acceptance probability varies with x
图2. 接受概率随x变化
出一系列的相关性等问题,于是尝试改进建议概率分布,下面采用随机游走算法对建议概率分布进行改进。此时随机游走算法的分布为对称分布,这里取建议概率分布为简单随机行走分布,从
中抽样的样本值记为 Zt ,接受概率为
。
那么随机游走算法就变成了:
1) 首先从建议概率分布
抽样产生样本值
,记候选样本值
。
2) 接着按从均匀分布
的随机数u,如果
,则接受该建议的随机数Yt,即
,否则
。
3) 重复上述过程,得到一组仅依赖于上一个随机数并且与前面随机数无关的
随机序列。
4) 计算接受概率
。
例子
同上述例子,概率密度函数
,由直接抽样的变换算法抽样,样本值记为
,选取建议概率分布
通过计算得到接受概率为
。
结果详见图3和图4。
在这里,通过改进建议概率分布,采用了直接行走算法,这里选用最简单的随机行走均匀分布,也就是概率密度函数是完全已知的概率分布。下面,再给定初始值和随机行走因子。最终,得到了抽样效
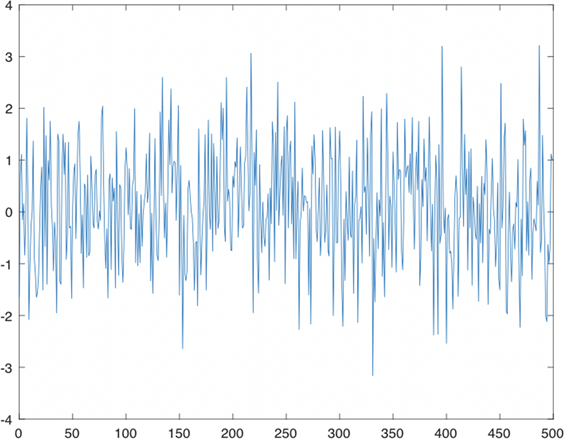
Figure 3. Acceptance probability varies with sample size
图3. 接受概率随样本数变化
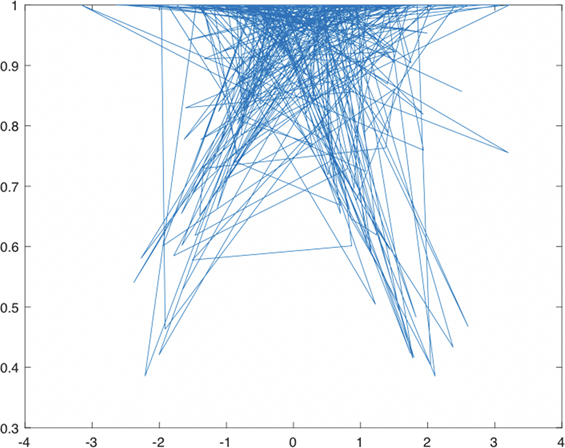
Figure 4. Acceptance probability varies with x
图4. 接受概率随x变化
率更高的抽样算法(程序见附录B)。
4. Gibbs方法
如果已知概率分布是全条件概率分布,则马尔可夫链状态转移的规则就是建立在全条件概率分布抽样基础上的,此时,使用全条件的抽样方法,使得抽样的结果满足随机性特点,同时每一步都是用全条件概率分布来构建马尔可夫链的。
Gibbs方法是将高维问题 [11] 化为一维问题,在对每个分量进行抽样的时候等价于对其他所有分量的条件分布进行抽样。所以下面将随机变量X分解成单随机变量
,随机变量X的概率分布
,单个随机变量
的全条件概率分布
其中,
表示
。
Gibbs算法就是
1) 将已知的概率分布分解为多个单变量的全条件概率分布。
2) 通过对多个单变量全条件概率分布中产生候选点,从
,其中,
中产生候选点
,更新
,来实现对已知概率分布的抽样。
例子
假设
[12] 是相互独立的服从指数分布的随机变量,且均值分别为1,2,3,4,5,然后
用模拟方法估计
,使用Gibbs算法。随机选择X,X,参数分别
,
(其中
,即
),求在 的情况下
的条件分布
,
。令初始状态
是和等于15的任意五个整数。从1,2,3,4,5中随机取出两个整数,
的情况下
的条件分布
,
。令初始状态
是和等于15的任意五个整数。从1,2,3,4,5中随机取出两个整数,
不妨假设是1和4,则在给定其他值下
和
的条件分布为在其和等于
,且参数为
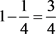 的指数分布值,下面令
的指数分布值,下面令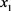 等于这个值,再重新设
的值使得
。重复上述过程就可以得
等于这个值,再重新设
的值使得
。重复上述过程就可以得
到概率值的估计。
5. 实例与应用
设
是一个带
域流的概率空间 [13] ,P为风险中性测度且服从
,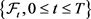 为P测度下产生的自然
域流。设St为股票价格,
,无红利美式股票卖权协议价格为K,期限为T,无风险利率r,
为股票波动率,
为标准布朗运动。令
为P测度下产生的自然
域流。设St为股票价格,
,无红利美式股票卖权协议价格为K,期限为T,无风险利率r,
为股票波动率,
为标准布朗运动。令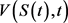 表示股票在时刻t的价格,所以我们可以构造一种投资组合来得到
,利用
对冲技巧,可以给出期权定价的数学模型,形成投资组合
,选取适当的
使得在
时段内,
无风险。设在时刻t形成的投资组合
表示股票在时刻t的价格,所以我们可以构造一种投资组合来得到
,利用
对冲技巧,可以给出期权定价的数学模型,形成投资组合
,选取适当的
使得在
时段内,
无风险。设在时刻t形成的投资组合
,并在
内,不改变份额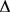 ,由于
无风险,在时刻
,投资组合的回报
,
,由于
无风险,在时刻
,投资组合的回报
,
即
。运用Itǒ公式,并且代入上式,得到Black-Scholes方程:
对于欧式看涨期权,也就是
,满足Black-Scholes方程的解为:
其中,
表示给定当前资产为
,资产价格S在期权到期日T时的密度函数。因此股票价格波动是一个随机过程,股票价格为
。其中,
为相互独立的服从 {Xt} 的随机变量。c表示该期权在零时刻的价格,因此
,由于这个期权是一种路径依赖的期权,计算包含一个多重积分,积分的维数为n,所以求解过程很复杂,因此采用马尔可夫链蒙特卡罗方法求解。
方法一:随机向量
,其概率密度函数为
,
式中,
。概率密度函数
归一化因子未知,是不完全已知概率分布,其抽样方法需要使用马尔可夫链蒙特卡罗方法。
此时,建议概率分布为
,随机方向d服从s维单位超球体上均匀分布,有
,
。
接受概率为
。
当前样本值为
,所以我们的算法如下:
1) s维单位超球体上均匀分布抽样产生随机方向d。
2)
抽样产生
,计算
。
3) 若
,
;否则,
。
方法二:取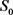 为零时刻的资产价格,
,那么n就是平均时所选取的时间周期数,h为时间增量,npath为仿真的路径数。我们模拟npath条路径,每一条路径都产生独立的收益。
为零时刻的资产价格,
,那么n就是平均时所选取的时间周期数,h为时间增量,npath为仿真的路径数。我们模拟npath条路径,每一条路径都产生独立的收益。
运用算法如下:
1) 取记号a1,a2,其中
,
,计算a1,a2;
2) 若
,则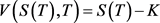 ,否则 V (S (T ),T ) = 0 ;
,否则 V (S (T ),T ) = 0 ;
3) 计算价格
。这里取利率
,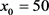 ,
,
,
,
,
,可以求解到股票价格
。
,
,
,
,
,
,可以求解到股票价格
。
6. 总结
由定义可知马尔可夫链是某一时刻取值当且仅当与之前相邻的一个时刻相关而与之前时刻没有联系,也就是它可以忘记过去,并且,当它经过一段时间的转移以后,就与初始时刻没有了联系,状态也会从非平稳到达平稳,马尔可夫链也就变得收敛。为了使得马尔可夫链尽快忘记初始状态,然后比较接近平稳状态,降低随机抽样的误差性,所以需要降低方差。因此,通过改变接受概率,减少模拟抽样的时间,加快收敛速度,从而达到较高的模拟效率。
通过随机模拟,可以将复杂的模型 [14] 简单化,以上示例显示了MCMC算法的便捷性,只要通过选择合适的建议概率分布,就可以很方便的构造平稳的马尔可夫链,并得到随机样本并估计出相关的参数值。
附录:
A 附录1
function [x,m] = rw(x0,a,iter)
x=x0;
for t=0:(iter+1)
y=rand () *2*a-a+x;
m=min(1, exp((x^2-y^2)/2));
u=rand ();
if u<=m
x=y;
end
end
x0=-4;
>> a=0.5;
>> n=500;
>> x=zeros(1, n+1);
>> iter= [0:1: n];
>> for t=0: n
plot(iter,x)
plot(x,m)
B 附录2
function [x,m] = rws(x0,a,iter)
x=x0;
for t=0:(iter+1)
u1=rand ();
u2=rand ();
u=rand ();
x=(-2*log(u1))^(1/2)*cos(2*pi*u2);
y=x+a*(2*u-1);
m=min(1, exp((-x^2+y^2)/2));
if u<=m
x=y;
end
end
x0=-4;
>> a=0.5;
>> n=500;
>> x=zeros(1, n+1);
>> iter=[0:1: n];
>> for t=0: n
plot(iter,x)
plot(x,m)
C 附录3
function [price1, price2, x]=MCMC(r,x,sigma,T,n,npath,K)
h=T/n;
xc=0;
a1=exp((r-0.5*sigma^2) *h);
a2=sigma*sqrt(h);
s1=0;
s2=0;
for i=1: npath
z=normrnd (0,1);
x=x*a1*exp(a2*z);
xc=xc+x;
i=i+1;
end
if x>K
R=x-K;
else
R=0;
end
s1=s1+R;
s2=s2+R^2;
theta=s1/npath;
stderr=sqrt((s2-s1^2/npath)/npath/(npath-1));
if x-K>0
price1=exp(-r*T) *theta;
price2=0;
else
price2=exp(-r*T) *stderr;
price1=0;
end
price1 =
25.2245
price2 =
0
x=
6.6300e+05