1. 引言
在1957年,数的表示理论中一种新的表示方法——β-展开被Renyi [1] 首次提出。之后,β-展式的丢番图理论和遍历性质被很多人深入研究。令β是大于1的任何实数,定义β-变换
,
,
其中
表示不超过x的最大整数,
表示数x的小数部分。
那么,任意一个实数
都可以把它展成一个如下形式的有限或者无限的序列:

对于任意的
,
,
。我们把式叫做x的β-展式,记为序列
[2] 。而且,Parry [3] 刻画了序列可允许性。之后,我们又了解到当
,x的β-展式是最终周期的当且仅当
。设 是一个Pisot数,那么x的β-展式是最终周期的当且仅当
(其中
是表示包含
和β的最小的域) [4] [5] 。
是一个Pisot数,那么x的β-展式是最终周期的当且仅当
(其中
是表示包含
和β的最小的域) [4] [5] 。
任意实数x可以唯一地被展成
。在求和中β的非负幂部分叫做x的β-整数部分,记作
;β的负幂部分叫做x的β-分数部分,记作
。如果x的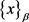 为0,即只有β的非负幂部分,我们把x叫做β-整数。用
来表示所有的β-整数的集合,也就是说
为0,即只有β的非负幂部分,我们把x叫做β-整数。用
来表示所有的β-整数的集合,也就是说
。
当
时,我们知道
[6] 。
定义1.1:定义
,
,
,
其中
表示不超过x的最大β-整数。
因此,对于任意的非负实数x都有如下形式的β-连分数展式:
,
,
其中
。
2. 定理及证明
定义2.1:给定β是大于1的任意实数,对任意的
,
,令
,
,
,
,定义
对于任意的
,把
叫做x的n阶β-渐近分数。
注2.2:由上述定义可以看出:由于
,故序列
单调递增且
。
命题2.3:对任意的
,我们有
。
证明:把定义2.1中式的左右同时乘以
,便得到
,
类似的,把式的左右两边同时乘以
,便得到
。
那么可得
。
推论2.4:对任意的
,有
。
证明:把命题2.3中的式子左右两边同时除以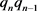 便可得到
便可得到
。
注2.5:由推论2.4可以看出,每一个奇数阶的β-渐近分数都大于紧接着它的那个偶数阶的β-渐近分数。
命题2.6:对任意的
,有
。
证明:把定义2.1中式的左右两边同时乘以
,便得到
,
同样的把式的左右两边同时乘以
,便得到
。
那么可得
。再由命题2.3得到:
。
推论2.7:对任意的
,有
。
证明:把命题2.6的左右两边同时除以
得到:
。
注2.8:由推论2.7可以看出,偶数阶的β-渐近分数形成递增序列,奇数阶的β-渐近分数形成递减序列。显然,把推论2.4和推论2.7结合得到:任何奇数阶的β-渐近分数必大于任何偶数阶的β-渐近分数。
定理2.9:对任意的
,序列
收敛。
证明:由推论2.4可知:
因为
是交错级数,由Libniz判别法知级数收敛,即
存在,故序列
收敛。
命题2.10: [7] 对于任意的
,
,那么有
。
定理2.11:设
是x的n阶β-渐近分数,则 。
。
证明:
 。
。
当n趋于无穷时,
趋于0,因此
。