民用高层建筑翻弯跨越交叉管道应力研究

Research on Stress of Turning over Crossing Pipes in Civil High-Rise Buildings

摘要: 民用高层建筑复杂的管线很容易引发同水平面不同管道交叉的问题，而翻弯跨越交叉管道的处理方式成为较为合理的处理方法，因此针对上述方法的管道应力分布开展研究有相当的必要性。本文对采用上下90˚、120˚与135˚翻弯跨越的管道的应力分布进行研究，得出结论：一次最大应力点为前后直管段支吊架点，且随着翻弯角度增大，应力水平逐渐降低，以限制一次应力为目的时135˚翻弯为最佳选择；同等温度条件下，翻弯角度越大，二次应力越大，以限制二次应力为目的时90˚翻弯为最佳选择。

Abstract: The complicated pipelines of civil high-rise buildings can easily lead to the problem of crossing different pipelines in the horizontal plane. And turning over the intersecting pipeline becomes a more reasonable countermeasure. Therefore, it is quite necessary to carry out research on the pipeline stress distribution of the above method. In this paper, the stress distribution of pipelines spanning 90˚, 120˚ and 135˚ is studied. It is concluded that the maximum stress point is the front and rear straight pipe supporting hanger points, and when the turning angle is increased, the stress level is gradually reduced, and the 135˚ turning is the best choice for the purpose of limiting the primary stress. Under the same temperature condition, the larger the turning angle is, the larger the secondary stress is, so as to limit the secondary stress. 90˚ turning is the best choice for the purpose.

1. 引言

在民用高层建筑设计施工中，各类管道设计铺设为非常重要的一环。而随着社会经济的快速发展，民用高层建筑的功能越来越复杂，新要求、新技术不断涌现 [1] ，管线铺设的复杂程度逐渐上升，很容易引发管道交叉的问题。因此针对管道交叉处理的研究有相当的必要性。

已有多名学者就管道交叉问题进行研究。张延斌 [2] 、张伟中 [3] 与张雨飞 [4] 等针对市政排水管道交叉问题，并提出了双孔法、暗渠法与倒虹管法等相应处理措施；刘丰 [5] 等对海底管道交叉进行了研究，提出了水泥压块直接覆盖处理法、水泥垫墩支撑跨越处理法、水泥灌浆包修正处理法与受限制区域交叉点处理法等措施；霍文星 [6] 等针对海底管道交叉问题，介绍了斜拉跨越技术的应用；雷新义 [7] 针对埋地管道直埋供热管道相交问题进行了研究，提出了上翻弯跨越的解决方案。

虽然管道交叉处理已经历诸多研究，且研究对象虽包含于海底管道、市政管道、埋地管道等诸多行业，但对于建筑内，尤其是民用建筑内管道交叉研究较为匮乏。另外研究主要集中于采用空间交错来解决问题，且研究以方法介绍为主，具体研究较少。对于同水平面管道交叉的翻弯跨越处理而言，管道应力分布研究较少，对于实际工程缺乏指导作用。本文针对民用建筑同水平面管道交叉翻弯跨越处理开展研究，为管道设计提供参考。

2. 工况参数确定与模型建立

2.1. 管道基本参数确定

本文主要考察背景为民用高层建筑的管道，因此管道基本参数的设定要代表普遍意义上的建筑管道共性并重点突出高层建筑较为突出的特点。故流动介质选取为水，相应流体密度对应为水的标准状态密度。由于目前国内超高层民用建筑项目中管道二次侧压力已经存在5.0 MPa (美国ASME标准)的情况，基于实际情况考虑，压力P1取5 Mpa以模拟最高管道压强下的管道情况。由于民用建筑中作为流动介质的水主要用于生活用途，因此温度取T1、T2、T3、几个特征点，分别为35℃、50℃与65℃。在管道走向确定的情况下，管径、壁厚、腐蚀余量、材质等参数主要影响应力计算数值而不影响应力分布规律，因此取常见情况即可。总体管道基本参数设定见表1。

2.2. 载荷工况确定

排除额外干扰，本文不考虑均布载荷、集中载荷以及附加位移等一系列其他因素的影响，仅考虑温度T1~T3及管道压强P1的影响。最终确定管道载荷工况组合如表2，其中L1-SUS工况表示安装态(安装温度21℃)的管道载荷，用于研究一次应力及各组成的变化规律；L2-L4-OPE工况用于表示3种不同温度下的实际操作载荷工况，L5-L7-EXP表示3种不同温度下的纯热态载荷，用于研究二次应力的变化规律。

Table 1. Basic parameters of the pipeline

表1. 管道基本参数

Table 2. Combination of Pipe load cases

表2. 管道载荷工况组合

2.3. 物理模型建立

本文针对民用建筑同水平面管道交叉翻弯跨越处理进行研究，为排除其余管段对研究管段的干扰，只关注翻弯跨越实际发生的管段。而对于翻弯管段而言，虽然涉及翻弯管与不动管(翻弯管避让的另一条管线)，但由于两管之间不发生物理碰撞，因此无论两管间以何种角度完成交叉跨越，研究对象只需要选取翻弯管即可。考虑到管道翻弯的影响可能会发生传递，因此除翻弯管段外，与之相邻的前翻弯管段、后翻弯管段亦予以保留。为排除水平面弯曲对研究产生的干扰，翻弯管不设置水平面上的弯头。对于翻弯管而言，最主要的决定因素归结于翻弯的角度。出于实际设计与现场加工实际情况的考量，翻弯管跨越部分与水平面保持平行且以跨越部分圆切面为对称面，翻弯管前后对称。这样原本翻弯角度的4个独立变量简化为1个变量。

基于以上分析，将复杂的实际翻弯跨越管段简化，最终的物理模型分为前直管段、翻弯管段、后直管段三部分。以每段管道编号起点指向终点的方向为+X向，竖直向上方向为+Y向，Z向由右手定则确定。为保证翻弯角度的影响能够被完整观察，每段管道前直管段与后直管段长4.5米。翻弯管段总长3.9米，高0.9米，保证翻弯管能跨越最大为DN800的不动管，以适应大部分情况。翻弯角度依据两段管道所夹角度确定且从前到后4个弯头依次编号为WT1~4。考虑现场管道弯曲加工的实际情况与可能性，本文共取90˚、120˚及145˚三个典型翻弯角度。对于翻弯跨越而言，其目的就是以避让管线在高度方向的变化避免同一水平面上的物理碰撞，每个角度均设置上翻弯与下翻弯两种情况，分别模拟翻弯管在空间上从上方与下方穿越的可能情况。所有管道首尾设置全固定以隔绝研究对象以外的管道的影响。90˚上翻弯管段及管道整体模型见图1(a)，120˚、145˚上翻弯管段模型见图1(b)、(c)。下翻弯模型仅在于翻管管段向−Y方向凸起，其余与对应角度上翻弯模型一致。上翻弯90˚、120˚、135˚依次编号模型A~C；下翻弯90˚、120˚、135˚依次编号模型D~F。

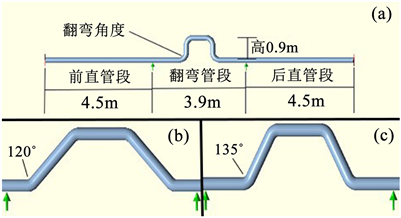
Figure 1. (a) 90˚ upturned pipe section and overall model of the pipeline; (b) 120˚ upturned pipe section model diagram; (c) 135˚ upturned pipe section model diagram

图1. (a) 90˚上翻弯管段及管道整体物理模型图；(b) 120˚上翻弯管段物理模型图；(c) 135˚上翻弯管段物理模型图

2.4. 管应力计算模型

依据选取的管道应力校核标准ASMEB31.3 [8] ，本文采用的应力计算模型如下所述。

对于一次应力，通常表示为：

$S_L={\left[I_a{\left(\left|S_{lp}+F_{ax}/A_p\right|+S_b\right)}^2+4S_{{}_t}^2\right]}^{1/2}<S_h$ (1)

对于二次应力，通常表示为：

$S_E={\left[{\left(\left|i_a{F}_{ax}/A_p\right|+S_b\right)}^2+4S_{{}_t}^2\right]}^{1/2}<f\left[1.25\left(S_c+S_h\right)-S_L\right]$ (2)

其中：

S_L为综合应力；

S_lp为纵向压应力，计算公式为：

$S_{lp}=P{D}_i^2/\left(D_o^2-D_i^2\right)$ (3)

D_i、D_o分别为管道内直径与外直径；

F_ax为轴向力；

A_p为管道横截面积；

I_a为持续轴向应力系数；

S_h为材料在设计温度下许用应力；

S_c为环境温度下许用应力；

S_b为弯曲应力，计算公式为：

$S_b={\left[{\left(I_i{M}_i\right)}^2+{\left(I_o{M}_o\right)}^2\right]}^{1/2}/Z$ (4)

M_i、M_o分别为平面内、外弯矩；

I_i、I_o分别为平面内、外应力增强系数；

Z为管截面模量；

S_t为扭转应力，计算公式为：

$S_t=I_t{M}_t/2Z$ (5)

M_t为扭转力矩；

I_t为扭转力矩系数。

3. 计算结果分析

3.1. 管道翻弯应力总体分析

图2显示了L1载荷工况上、下翻弯90˚的综合应力分布情况，弯头区域应力水平以弯头中心点代表。由图2可以看出，由于前后直管段均受到全固定限制的影响，应力水平出现反复波动，因此主要观察范围集中于翻管管段部分。翻弯管段综合应力整体呈对称分布，且可以分为三部分：第一部分由前直管段支吊架点至WT1；第二部分由WT1至WT4；第三部分由WT4至后直管段支吊架点。每部分均表现出先降后升的变化趋势。对于整体翻弯管段而言，最大应力点出现在前后直管段支吊架点，为45.268 Mpa/44.954 Mpa。对于同一翻弯管道的四个弯头而言，WT1与WT4两弯头综合应力水平(41.275 Mpa/40.753 Mpa)高于WT2与WT3两弯头综合应力水平(39.076 Mpa/38.738 Mpa)。上、下翻弯90˚的总体应力对比显示出下翻弯90˚总体应力高于上翻弯90˚。图3显示了上、下翻弯90˚的轴向应力分布情况，由图3可以看出，下翻弯90˚轴向应力要总体高于上翻弯90˚，且两者轴向应力呈现相反的变化趋势。上翻弯90˚时翻弯管段轴向应力变化呈现下凹趋势，WT1与WT4轴向应力为38.814 Mpa，大于直管段平均值38.710 Mpa且为轴向应力最大值点；WT2与WT3轴向应力为38. 675 Mpa，小于直管段平均值38.710 Mpa且为轴向应力最小值点。下翻弯90˚时翻弯管段轴向应力变化呈现上凸趋势，WT2与WT3轴向应力为38.430 Mpa，大于直管段平均值38.396 Mpa且为轴向应力最大值点；WT1与WT4轴向应力为38.291 Mpa，小于直管段平均值38.396 Mpa且为轴向应力最小值点。上、下翻弯90˚弯曲应力变化曲线几近一致且应力数值小一个数量级，故不再详述。

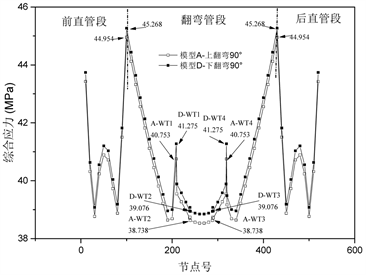
Figure 2. Comprehensive stress distribution diagram of 90˚ up and down turning under L1 load conditions

图2. L1载荷工况上、下翻弯90˚的综合应力分布图

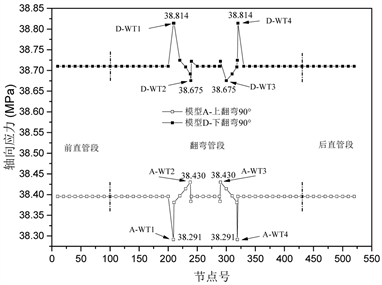
Figure 3. Axial stress distribution diagram of 90˚ up and down turning under L1 load conditions

图3. L1载荷工况上、下翻弯90˚的轴向应力分布图

由图2、3可以看出，综合应力翻弯管段的变化趋势主要受轴向应力的影响，其最大应力点出现在直管段支吊架点，总体最大应力点出现在前后直管段支吊架点，因此管段一次应力薄弱点为翻弯管段的前后支吊架点。由于弯头为管道薄弱环节，因此后续工作仍将弯头纳入考虑。弯头最大应力点出现在WT1与WT4。由于整体呈对称分布，本文取前直管段支吊架点与WT1进行后续分析。

3.2. 翻弯角度影响

图4~7分别显示了L1载荷工况下前直管段支吊架点与WT1点轴向应力、弯曲应力、综合应力与一次应力比率随翻弯角度变化情况。

对于WT1而言，随着范围内角度由90˚增加至135˚，上下翻弯弯曲应力、综合应力与综合应力比率均表现出先降低后升高的变化趋势，最小弯曲应力、综合应力与最小一次应力比率点出现在120˚翻弯角度点，分别为1.496 Mpa/39.411 Mpa/28.600% (上翻弯)，1.496 Mpa/39.937 Mpa/29.000% (下翻弯)。上下翻弯轴向应力呈现出总体相反的变化趋势，随着角度逐渐增大，上翻弯轴向应力呈下降态势，由38.291 Mpa下降至38.273 Mpa；而下翻弯轴向应力呈上升态势，由38.814 Mpa上升至38.833 Mpa。对上下翻弯进行对比，上翻弯轴向应力、综合应力与一次应力比率均小于下翻弯，而二者弯曲应力一直保持相等。

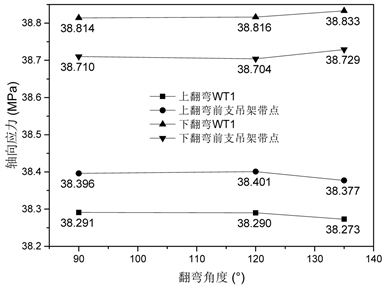
Figure 4. Variation diagram of axial stress varied with turning angle

图4. 轴向应力随翻弯角度变化图

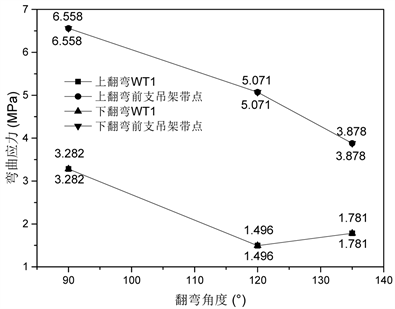
Figure 5. Variation diagram of bending stress varied with turning angle

图5. 弯曲应力随翻弯角度变化图

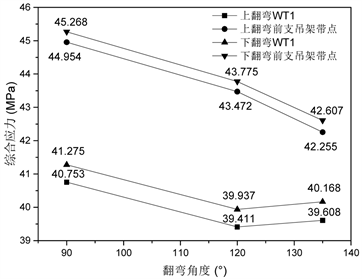
Figure 6. Variation diagram of comprehensive stress varied with turning angle

图6. 综合应力随翻弯角度变化图

Figure 7. Variation diagram of primary stress ratio varied with turning angle

图7. 一次应力比率随翻弯角度变化图

对前直管段支吊架点而言，轴向应力变化趋势与WT1对应指标相比呈现不同变化趋势，上翻弯是呈现先增后降的趋势，下翻弯则呈现先降后升的趋势。而弯曲应力、综合应力与综合应力比率呈现持续下降的趋势，且变化呈现先慢后快的特点。对上下翻弯进行对比，上翻弯轴向应力、综合应力与一次应力比率均小于下翻弯，而二者弯曲应力一直保持相等。而对前直管段支吊架点于WT1各项指标数值对比，前直管段支吊架点均高于WT1。

图4~7表明，对于弯头而言，随着翻弯角度增大，综合应力与一次应力比率先下降后上升，120˚翻弯综合应力处于最小水平；而对前直管段支吊架点而言，随着翻弯角度增大，综合应力与综合应力比率呈现持续下降。如果进一步增大翻弯角度，前直管段支吊架点应力可能会进一步下降，在某个角度会使得弯头应力超过前直管段支吊架点应力成为最大应力点。不过限于实际情况，翻弯角度不会过大。因此以限制一次应力为目的的话，135˚翻弯为较好选择。

3.3. 温度的影响

温度的影响主要体现在二次应力的变化上。图8与图9分别显示了温度变化对前直管段支吊架点与WT1点的二次应力影响情况。由于上下翻弯对二次应力变化不产生影响，因此图8与图9中不再对各翻弯角度上下翻弯进行区分。

Figure 8. Variation diagram of secondary stress ratio varied with temperature in the support hanger point of the front straight pipe

图8. 前直管段支吊架点二次应力比率随温度变化图

Figure 9. Variation diagram of secondary stress ratio varied with temperature in the support hanger point of the WT1

图9. WT1点二次应力比率随温度变化图

由图8与图9可以看出，90˚、120˚翻弯时二次应力比率随温度增大呈线性上升，所不同的是随着翻弯角度由90度上升至120˚，WT1点二次应力线性变化斜率明显增大，而前直管段支吊架点斜率变化微小。而对于135˚翻弯，前直管段支吊架点与WT1点二次应力比率均表现出不同于90˚、120˚翻弯时的变化趋势。随着温度升高，两点二次应力比率均表现出在35℃~50℃阶段线性下降，50℃~65℃阶段线性上升的态势。纵向比对，总体上温度越高，二次应力越大。同温度、翻弯角度下WT1二次应力大于前直管段支吊架点且WT1二次应力增长比率快于前直管段支吊架点,说明二次应力薄弱点在弯头部分。同温度下翻弯角度越大，二次应力越大，且WT1二次应力增长比率快于前直管段支吊架点。

由图8与图9可以看出，二次应力最大点为WT1。对于135˚翻弯而言，50℃时二次应力处于最低水平，但随着温度的不断提升，90˚翻弯二次应力比率增长最为缓慢，因此高温条件下90˚翻弯二次应力安全性较好。

4. 结论

本文针对民用建筑同水平面管道交叉翻弯跨越处理开展研究，对管道翻弯角度以及温度对应力水平的影响进行了分析，通过改变不同的翻弯角度与温度，并得到如下结果：

1) 由应力水平可以看出，一次应力薄弱点为前后直管段支吊架点，二次应力薄弱点为弯头WT1与WT4。对于已经建成的管道翻弯而言需要进行重点关注。

2) 随着翻弯角度的增大，前后直管段支吊架点代表的一次应力最大值上呈现下降趋势而弯头WT1与WT4点则在120˚取得最小值，因此选择大翻弯角度有利于降低一次应力水平。

3) 同等温度条件下，翻弯角度越大，二次应力越大。因此选择小翻弯角度有利于降低二次应力水平。

4) 总体上随着温度的上升，二次应力呈现增大的趋势。但135˚翻弯在小于50℃下呈现相反变化趋势，值得进一步研究。

在温度较低时，主要关注一次应力问题，因此135˚翻弯为较好选择。此外，翻弯角度过大会使翻弯段占据过大空间而不具备实用性，结合加工制造的实际情况，大于135˚翻弯不具备实用性，因此135˚翻弯为最优选择。但温度较高时，二次应力成为主要问题，因此90˚翻弯会成为更好的选择。