1. 引言
材料力学理论及相关实验对于材料类、机械工程类及土木建筑类的学生十分重要,是其今后工作和学习的重要基本技能之一。目前该实验的教学手段通常采用万能材料实验机对给定测试材料进行拉伸实验、压缩实验及扭转实验等,使学生掌握操作技巧及验证材料的力学性质;另外一些主流的材料力学虚拟仿真软件采用三维交互式操作,可仿真真实实验的操作要点及植入实验数据以反馈学生的操作,以上两种方法对提高学生的动手能力及测量方法十分重要,但是对学生深层次理解材料力学性质差异产生的根源略显不足,同时也不利于学生探索极端条件下材料的性质。因此,需要开发一种新的实验手段或仿真过程进行补充。常规实验测试材料一般选铁基材料进行测量,本项目为提高学生的学习兴趣采用近期最热门的石墨烯材料进行仿真实验,石墨烯不仅能提高学生的学习兴趣,而且因为其为二维材料,会更有利于学生观察应变过程中材料的微观变化,因此,本项目以石墨烯为测试载体旨在为材料力学实验提供一种深度理解的解决途径。
石墨烯(Graphene),又称单原子层石墨,由于其具有极优的力学性能、良好的电学性能以及较优的热学性能成为目前最具应用前景的一种新型纳米材料。石墨烯已经在复合材料 [1] 、光学电池 [2] 、传感器件 [3] 、催化剂 [4] 等诸多领域应用并具有广阔的应用前景 [5] [6] [7] [8] 。理想的石墨烯是由碳原子以sp2杂化方式形成的单层六方蜂窝状平面薄膜,其中,C-C键长约为0.1426 nm [9] ,然而,由于生产技术及制备工艺的限制,实际生产中几乎无法获得完美的石墨烯,常规方法制备出的石墨烯中常伴有各种缺陷,如:空位缺陷、Stone-wales缺陷、增原子缺陷等 [10] [11] 。研究发现,这些缺陷对石墨烯的力学性能 [12] 、电学性能 [13] 以及热学性能 [14] 都具有一定的影响 [15] [16] [17] 。因此,石墨烯缺陷的研究对石墨烯实际应用具有十分重要的现实意义和理论价值。
近年来,许多研究者对单层石墨烯的力学及电学等性能进行了大量研究。谭新君等 [18] 对石墨烯薄膜的杨氏模量进行研究,结果表明:石墨烯的理论杨氏模量为1.00 TPa。张霖等 [19] 对单层石墨烯薄膜的纳米压痕进行了分子动力学的计算,结果表明,石墨烯材料的半径主要影响压痕过程中的临界深度,而对临界载荷、弹性模量和破坏应力的影响不大。
石墨烯的结构、力学性能(尤其是拉伸性能)、电学性能及热学性能的实验研究及理论研究均已经十分充分,本文采用经典的分子动力学的方法,对完美的和含有空位缺陷的锯齿型和扶手椅型单层石墨烯的撕裂性能进行了计算数值模拟,研究了空位缺陷对石墨烯撕裂力学性能和变形机制的影响。
2. 计算方法及物理模型
本工作的目的虽然是为教学演示石墨烯的撕裂微观过程,但也需要保证计算的可靠性及计算精度,由于分子动力学计算模拟精度十分依赖所选用的势函数的精度,本工作采用LCBOP (the Long-range Carbon Bond Order Potential)结构势函数 [20] 来描述石墨烯中碳原子之间的相互作用,具体表达形式如下:
其中,
表示系统的总结合能,i、j分别指单个的原子
表示短程原子效应的能量,
表示远程原子效应的能量,其中,
表示开关函数。
、
具体表达式如下:
、
分别表示原子i和原子j之间的排斥力和吸引力,作用力类型主要取决于原子间距,
表示键序。
是截断函数,随距离
的增加从1衰减到0,表示原子i与其最近邻原子间的相互作用。
材料的结构及缺陷是材料类学生必须掌握的基本知识,为加深学生对晶体学方面知识,本工作选取了锯齿型石墨烯和扶手椅型石墨烯中最为典型的空位缺陷。分子动力学模拟计算中选用的锯齿型石墨烯和扶手椅型石墨烯结构模型如图1所示。在锯齿型和扶手椅型石墨烯薄膜中分别布置一个单原子缺陷位和两种类型的双原子缺陷位,具体原子缺陷位如图2所示。为了全面研究不同缺陷对石墨烯撕裂性能的影响,本工作采用8个不同缺陷的石墨烯理论模型,其中四个锯齿型模型尺寸为:62.7531 nm × 74.1078 nm,四个扶手椅型模型尺寸为:74.1078 nm × 62.7531 nm。不同模型所包含的的原子数量分别为:完美石墨烯模型包含1800个原子,单原子空位缺陷石墨烯模型由1799个碳原子组成,双原子空位缺陷石墨烯碳原子数量为1798个。
本工作采用分子动力学软件包LAMMPS [21] (Large-scale Atomic Molecular Massively Parallel Simulator)进行模拟,结果分析使用可视化软件OVITO [22] 来进行显示和分析;模拟过程中系统温度保持在250 K恒定,模拟时间步长为1 fs。模型采用X、Y方向上为非周期性边界条件,Z方向上为周期性边界条件;首先进行10,000步体系结构弛豫,使体系能量最低,达到稳定状态,然后进行撕裂模拟,撕裂速度为0.03 angstroms;计算过程选用NVT和NVE系综,用NVE系综模拟加载过程,沿XY平面往Y方向施加撕裂;通过Nose-Hoover [23] [24] 热浴方法控制系统温度为250 K恒定。
3. 计算结果及分析
3.1. 空位缺陷对石墨烯撕裂力学性能的影响
完美的、含有单原子空位缺陷和两种类型的双原子空位缺陷的锯齿型和扶手椅型石墨烯的撕裂应力
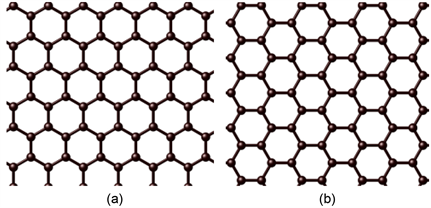
Figure 1. Physical model of single-layer graphene film. (a) serrated type; (b) armchair type
图1. 单层石墨烯薄膜物理模型。(a) serrated type; (b) armchair type

Figure 2. Schematic of the vacancy defects in single-layer graphene films. (a) single-atom vacancy defect; (b) double-atom vacancy defect I; (c) double-atom vacancy defect II
图2. 石墨烯的原子空位缺陷示意图。(a) single-atom vacancy defect; (b) double-atom vacancy defect I; (c) double-atom vacancy defect II
—应变关系曲线如图3所示,由图可以看出,当锯齿型石墨烯应变量小于1.25%时,石墨烯应力随应变呈线性增长,石墨烯处于弹性变形,应变消失后并不影响石墨烯的结构;当应变量在1.25%~2.5%的范围内时,石墨烯应力处于屈服阶段,此时应变在很小的范围内波动,但应力却不断增大;当应变量超过2.5%之后,石墨烯应力处于强化阶段,石墨烯同时具有弹性变形和因为断裂而产生的塑性变形,但是在应变量增大的过程中,弹性变形逐渐消失,只留下塑性变形。锯齿型石墨烯缺陷的存在对其断裂时应变的影响不大,但它使断裂最大强度明显小于完美锯齿型石墨烯的最大强度。扶手椅型石墨烯的应力—应变曲线趋势与锯齿型石墨烯的大体一致,但是在扶手椅型石墨烯的强化阶段出现了锯齿型石墨烯所没有的应变量在增加,应力却减小的“缩颈”现象结合表1可知。
对于锯齿型石墨烯薄膜,单原子空位缺陷使石墨烯薄膜的抗撕裂强度下降8.59%,两种类型的双原子空位缺陷使其抗撕裂强度下降8.11%和7.58%,单原子空位缺陷的影响稍大于双原子空位缺陷的影响。对于扶手椅型石墨烯薄膜,单原子空位缺陷使石墨烯薄膜的抗撕裂强度下降1.56%,两种类型的双原子空位缺陷则使其抗撕裂强度上升了2.42%和3.55%,这与对锯齿型石墨烯薄膜都是造成强度下降的影响不同。
空位缺陷同时也对石墨烯薄膜撕裂极限应变也有一定程度的影响。对于锯齿型石墨烯薄膜,单原子空位缺陷使极限应变上升48.63%,两种类型的双原子空位缺陷使极限应变上升了51.86%和51.32%,空位缺陷对锯齿型石墨烯薄膜的撕裂极限应变有显著的影响,其中,与抗撕裂强度相反的是,双原子空位缺陷的影响略大于单原子空位缺陷的影响。对于扶手椅型石墨烯薄膜,空位缺陷均使石墨烯的撕裂极限应变降低。单原子空位缺陷、两种类型的双原子空位缺陷的撕裂极限应变下降幅度分别为13.79%、16.74%和22.16%。与锯齿型石墨烯薄膜相同的是,双原子空位缺陷对扶手椅型石墨烯薄膜的撕裂极限应变的影响要略大于单原子空位缺陷对其的影响。
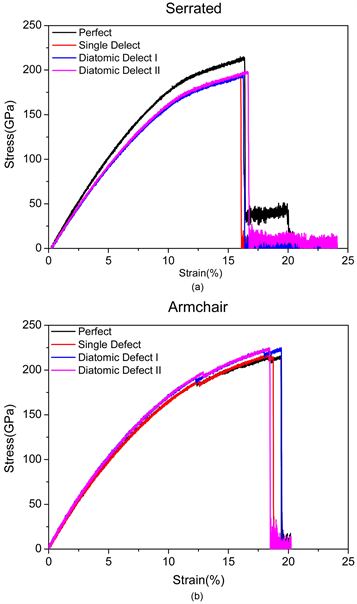
Figure 3. Stress-strain curves of serrated and armchair-type single-layer graphene films with vacancy defects. (a) serrated type; (b) armchair type
图3. 含不同空位缺陷单层石墨烯薄膜的撕裂应力—应变曲线。(a) serrated type; (b) armchair type

Table 1. Effect of vacancy defects on the tearing mechanical properties of single layer graphene films (unit: Stress: GPa Strain: %)
表1. 空位缺陷对单层石墨烯薄膜基本撕裂力学性能的影响(单位:应力:GPa,应变:%)
3.2. 空位缺陷对石墨烯变形的影响
完美的石墨烯薄膜的变形首先形成于薄膜的边缘处,如图4所示。但是对于有空位缺陷的石墨烯薄膜,变形的方式,尤其是变形开始的位置,与完美的石墨烯薄膜不同。
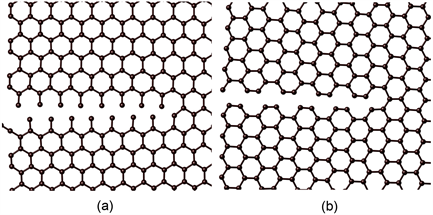
Figure 4. Local atomic structure of tearing perfect single-layer graphene films. (a) serrated type; (b) armchair type
图4. 完美的石墨烯薄膜撕裂时的局部原子构型。(a) serrated type; (b) armchair type
图5显示了有空位缺陷的石墨烯薄膜在撕裂作用下开始出现变形及断裂时的原子构型,发现无论是锯齿型石墨烯薄膜还是扶手椅型石墨烯薄膜,新的变形的产生位置均出现在单原子空位缺陷或者双原子空位缺陷的附近。
3.3. 温度对石墨烯薄膜的影响
温度对材料力学性能的影响是十分显著的,表征了石墨烯撕裂性质对温度的依赖,本文对石墨烯在不同的温度的撕裂性质进行了分子动力学研究。通过改变测试环境下的温度,即可得到不同温度下完美石墨烯的撕裂性质。
由图6可知,随着温度的升高,完美的锯齿型和扶手椅型石墨烯薄膜的撕裂强度不断下降。其中,扶手椅型石墨烯薄膜的下降幅度较大,且呈持续下降趋势。而锯齿型石墨烯薄膜的下降趋势略为曲折:当温度从300 K上升到500 K以及从1100 K上升到1300 K时,石墨烯薄膜的下降幅度都较小;当温度从500 K上升到700 K时,其下降幅度突然增大;当温度从700 K上升到900 K时,锯齿型石墨烯薄膜的应力-温度曲线呈上升趋势,且上升幅度较大,在下一升温阶段曲线又呈较大幅度的下降趋势。
3.4. 撕裂时石墨烯不同原子受力
如图7所示,撕裂时力在石墨烯薄膜上的具体方向虽各有不同,但是大体上都是往空位缺陷的外部
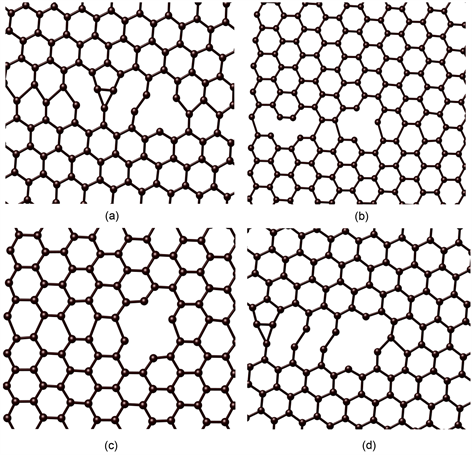
Figure 5. Local atomic structure of tearing vacancy defects single-layer graphene films. (a) serrated type with single-atom defect; (b) armchair type with single-atom defect; (c) serrated type with double-atom vacancy defect; (d) armchair type with double-atom vacancy defect
图5. 有空位缺陷石墨烯薄膜断裂时的局部原子构型。(a) serrated type with single-atom defect; (b) armchair type with single-atom defect; (c) serrated type with double-atom vacancy defect; (d) armchair type with double-atom vacancy defect

Figure 6. Tearing stress-temperature curves of serrated and armchair-type perfect graphene films
图6. 完美的石墨烯薄膜的撕裂应力—温度曲线
施加力。通过对图7进行分析,发现在空位缺陷的附近部分原子受力较小,近乎没有;而在撕裂的方向上,可以看见原子受力较大,且大多指向空位缺陷的位置,具体受力见图7中的圆圈部分。
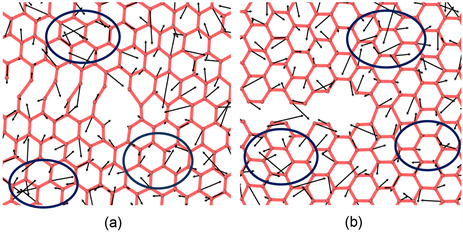
Figure 7. Schematic of the direction of force in tearing of two-atoms vacancy defects type II single layer graphene film
图7. 双原子空位缺陷II型石墨烯撕裂时受力方向示意图
4. 结论
本文采用经典分子动力学方法对完美或存在空位缺陷的扶手椅型和锯齿型单层石墨烯的撕裂性能进行了理论仿真,不同温度条件下完美石墨烯的撕裂性能的影响也不一样。通过本实验演示过程可以使学生掌握晶体学知识、分析应力应变曲线及由微观过程分析材料的应变过程和不同原子的受力,同时给出测试温度变化对材料力学性质的影响,使学生体会不同学科理论知识与实践的综合运用,对提高学生的理论认识深度具有十分重要的意义;由于本工作给出了不同形变过程时材料的微观变化过程,可使学生更深入地了解材料应力形成的根源,对今后研究材料的力学性质提供一种解决问题的思维方式;同时通过该仿真实验也可以使学生对材料的宏观力学性质对环境的依赖性有初步的认识。总之,该演示实验项目可以对常规力学实验进行有力补充,对材料力学实验教学及人才培养均具有十分重要的意义。
基金项目
海南大学教育教学改革项目(项目编号:hdjy1911);海南大学材料与化工学院教育教学改革项目(项目编号:Chjy1802)。
NOTES
*通讯作者。