1. 引言
在著名华人数学家丘成桐先生的领导下,利用分析与微分方程的方法研究微分几何已经成为一个重要的潮流,称为几何分析,其代表性工作之一是丘成桐利用几何分析的方法证明了卡拉比猜想与正质量猜想。在此基础上,几何分析学派蓬勃发展并取得了很多非常好的研究成果。微分流形的结构能够在多大程度上刻画其拓扑结构,其拓扑结构又如何影响其几何结构,以及如何通过几何不变量、几何估计、几何微分方程与其它几何条件来研究与分类重要的微分流形一直是微分几何的中心研究课题之一。上世纪80年代,Hamilton [1] 引进了以Ricci流为代表的几何发展方程的方法,通过对一些具有深刻几何背景的抛物型几何发展方程的研究来揭示黎曼流形的几何与拓扑结构,得到了许多重要的几何与拓扑结果。实际上,Hamilton最早引进Ricci流的主要目的是解决3维流形著名的Poincaré猜想(任意单连通的3维闭流形必同胚与3维闭球面)。虽然到现在Poincaré猜想已被证明 [2] [3] [4] ,但Ricci流作为研究黎曼流形最有力的工具之一,仍然有许多问题值得研究。其中一个非常重要的问题就是Ricci流的自相似解 [5] (即Ricci孤立子)的分类及几何结构,Ricci孤立子经常出现在Ricci流方程的奇异点经伸缩变换后的极限中 [6] [7] [8] [9] ,因而对其分类及几何量的研究可以更好的理解Ricci流的奇异结构及几何、拓扑结构。
1.1. Ricci孤立子介绍
黎曼度量
,若其Ricci张量满足
(
为常数),则称
为爱因斯坦度量。一个光滑流形
带有爱因斯坦度量,则称该流形为爱因斯坦流形,Ricci孤立子是爱因斯坦度量的自然推广。
光滑流形上一个完备度量
称为Ricci孤立子,若存在光滑的向量场
使其Ricci张量满足
为常数。此外,若
为一个梯度向量场,使得光滑函数
满足
则称
为梯度Ricci孤立子,光滑函数
称为Ricci孤立子的势函数。
由于
为度量
在方向
上的Lie导数,故上述Ricci方程分别可以写作
和
。
时称为稳定Ricci孤立子,
为收缩Ricci孤立子,
时称为扩张Ricci孤立子。
特别地,
(即
为常数函数)时,
为爱因斯坦度量,因此Ricci孤立子为爱因斯坦度量的自然推广,且经过适当的伸缩变换可标准化令
,
,
。
1.2. 典型的Ricci孤立子
众所周知,
时存在非平凡的紧致梯度收缩Ricci孤立子。同样的,也存在非爱因斯坦度量的完备非紧致Ricci孤立子,下面给出一些完备非紧致Ricci孤立子的典型的例子。
例1.1:(cigar孤立子) 2维流形上,Hamilton引进了第一个完备非紧致的稳定孤立子,称为cigar孤立子,其度量为
,势函数为
。特别地,cigar孤立子有正的高斯曲率及线性的体积增长。
例1.2:(Bryant孤立子)黎曼流形
的情况下,高维完备非紧致的梯度稳定孤立子由Bryant引进,Bryant孤立子旋转对称、具有正截面曲率且以
为半径的测地球
体积增长率为
。
例1.3:(Gaussian孤立子)具有平坦欧几里得度量的
也可以包含收缩及扩张Ricci孤立子,称为Gaussian收缩孤立子或扩张孤立子:
1)
为带有势函数
的梯度收缩孤立子,且
。
2)
为势函数是
的梯度扩张孤立子,且
。
2. Ricci孤立子的刚性
梯度Ricci孤立子为Hamilton-Ricci流的自相似解且对应于奇异模型,因此Ricci孤立子的分类对数学及物理的研究与发展都具有重要的意义,Ricci孤立子分类的关键是结合Ricci孤立子方程运用微分几何与几何分析的方法寻找与构造其上一些重要的几何不变量,建立一些有意义的几何估计、几何比较定理并计算一些拓扑不变量,最终结合黎曼几何与拓扑学的重要定理给出其分类结果。Ricci孤立子的研究主要分为紧致与非紧致两大部分,在流形紧致的条件下,Perelman [2] 证明了Ricci孤立子一定是梯度孤立子,因此对紧致Ricci孤立子的研究转化为对梯度Ricci孤立子的研究。特别地,紧致稳定或扩张Ricci孤立子必为爱因斯坦度量 [10] [11] ,且2、3维紧致收缩Ricci孤立子也是爱因斯坦度量 [11] 。类似的结论在高维情形未必成立,但对于具有正曲率算子的紧致收缩Ricci孤立子,Hamilton [5] (维数为3的情况), [12] (维数为4)及Böhm-Wilking [13] (维数大于4)证明了它一定是球面的有限商空间。在流形完备非紧致的条件下,又可以分为收缩、稳定、扩张的情形进行研究。其中有很多经典且重要的结果: [14] 中证明了完备收缩Ricci孤立子为紧致的当且仅当其上的向量场有界;曹怀东、陈兵龙和朱熹平 [15] 得到了没有任何曲率条件的收缩Ricci孤立子的完全分类结果(3维完备梯度收缩Ricci孤立子必为
,
,
的有限商空间);高维情形下,Petersen-Wylie [16] 证明了Weyl张量为零的
维梯度收缩Ricci孤立子若Ricci曲率有下界且满足一定的增长条件则一定是
,
,
的有限商空间;Ricci孤立子稳定时,Perelman猜想3维Bryant Ricci孤立子是唯一的完备非紧致k-非坍塌的稳定梯度Ricci孤立子,最近Brendle [17] 通过研究无穷远附近的渐近几何与Killing向量场最终证明了Perelman猜想;在高维情形,利用类似的方法Brendle [18] 还证明了具有正截面曲率与渐近圆柱条件的梯度稳定Ricci孤立子一定是旋转对称的;Ricci孤立子扩张时,在2维情形, [19] 中证明了存在非平凡的完备非紧致扩张Ricci孤立子;对于高维情形,曹怀东 [20] 构造了完备非紧致的Kähler-Ricci稳定孤立子。
特别地,一个完备的梯度Ricci孤立子称为刚性的若它等距于
的一个有限商空间,其中
为爱因斯坦流形。作为爱因斯坦流形的推广,Ricci孤立子自然会满足一些刚性性质。众所周知,并不是所有的梯度Ricci孤立子都是刚性的,本节我们将概括总结给出一些Ricci孤立子能满足刚性的条件。
Hamilton [1] (2维情形)及Ivey [11] (3维情形)证明了紧致Ricci孤立子为刚性的。在Ni-Wallach [21] 工作的基础上,Naber证明了任意具有非负曲率算子的4维完备收缩Ricci孤立子是刚性的,著名的Bryant Ricci孤立子表明存在具有正曲率算子的非刚性旋转对称的稳定及扩张梯度Ricci孤立子。此外不难看出,任意维紧致稳定及扩张梯度Ricci孤立子是刚性的。紧致流形其数量曲率为常数时为刚性的,更一般的,Petersen-Wylie [22] 证明了以下定理:
定理2.1:一个有平凡势函数
的紧致梯度Ricci孤立子
,若
,则
为刚性的。
非紧致的条件下,Perelman [3] 还证明了任意具有非负截面曲率的3维完备梯度收缩Ricci孤立子为刚性的。特别地,若一个孤立子是刚性的,则其径向曲率消失(即
),且数量曲率为常数。反过来,具有常数量曲率并满足径向平坦(
)只能得到紧致流形的刚性。非紧致的条件下,Petersen-Wang [23] 证明了如下结果:
定理2.2:一个梯度收缩(扩张) Ricci孤立子为刚性的当且仅当该孤立子有常数量曲率且为径向平坦的(即
)。
推论2.3:任意完备非紧致梯度收缩Ricci孤立子
,若其具有非负Ricci曲率并满足
,则
为刚性的。
若函数
可写为
,称
为可求长的,其中
为距离函数。对具有非负径向曲率的可求长收缩Ricci孤立子,Petersen [23] 证明了完备非紧致可求长的梯度收缩Ricci孤立子若具有非负径向截面曲率及非负Ricci曲率则为刚性的。此外他还证明了具有最大对称性的(齐次的)梯度Ricci孤立子也是刚性的。
利用Laplacian及f-Laplacian的最大值原理并假设Ricci张量非负且截面曲率满足一定的上界条件时,Lόpez-Río [24] 证明了梯度收缩Ricci孤立子刚性的一个充要条件:
定理2.4:令
为一个具有有界非负Ricci张量的完备梯度收缩Ricci孤立子,则
为刚性的当且仅当其截面曲率上界为
。
利用Weyl张量及数量曲率条件,Petersen-Wang [16] 还得到了梯度Ricci孤立子的一个刚性结果。
定理2.5:任意具有常数量曲率的梯度Ricci孤立子
,若
(即非稳定的)且其Weyl张量满足
,则
为刚性的。
接着Lόpez-Río [25] 还证明了任意
维紧致Ricci孤立子为刚性的当且仅当它具有调和Weyl张量;Munteanu-Sesum [26] 证明了任意具有调和Weyl张量的
维完备非紧致梯度收缩Ricci孤立子为刚性的;在此基础上,Yang-Zhang [27] 得到了一些新的结果:
定理2.6:令
为一个完备非紧致的收缩梯度Ricci孤立子,若
,则为
刚性的。
结合黎曼曲率条件及一定的Weyl张量条件,他们还证明了梯度收缩Ricci孤立子若满足
或
或
则为刚性的。
黎曼流形上的等周型不等式及其稳定性的研究不仅可以刻画流形上相关几何量的相互定量关系,而且根据其等号成立的条件也可以得到一些流形刚性的结果。利用势函数上下界的增长估计可以建立Ricci孤立子较弱条件下的等周不等式、平均值不等式、Sobolev不等式以及一些重要的几何积分不等式,并通过研究等号成立条件与不等式的稳定性也可以得到一些Ricci孤立子的刚性结果。
3. 体积增长估计
测地球的体积增长是研究微分流形及Ricci孤立子重要的几何性质,体积增长率是流形极为重要的几何不变量。具有非负Ricci曲率的完备非紧致黎曼流形
上,有两个关于测地球体积增长估计的重要定理:经典的Bishop体积比较定理表明测地球有至多欧氏体积增长(即存在常数
使得当
充分大时,有
);另一个定理表明测地球有至少线性体积增长(即存在正常数
,使得
)。对于Ricci孤立子,利用势函数的上下界估计及势函数水平集重要的几何性质,曹怀东和周德堂证明了收缩Ricci孤立子测地球至多欧式体积增长,而有关测地球体积的最少增长目前最好的结果为对数函数形式的增长。对比一般的黎曼流形,大家猜测Ricci孤立子体积最少增长的最佳结果也可能为线性增长形式。本节,我们将概括总结关于Ricci孤立子的渐近体积比及体积增长的上下界估计结果。
Hamilton [10] 系统地开发了Ricci流降低维数的研究方法。由Hamilton对2维Ricci流古典解的分类可知任意具有有界曲率的2维完备古典解都不能达到最大体积增长。在此基础上应用降维方法,Perelman [2] 证明了:
定理3.1:令
为一个
维完备非紧致的黎曼流形,假设
,
且
,
,
为具有非负曲率算子及有界曲率的Ricci流的一个非平坦古典解,则其度量的渐近体积比满足:
推论3.2:(Carrillo-Ni [28] )任意具有非负Ricci曲率
的非平坦梯度收缩Ricci孤立子其渐近体积比为零,即:
具体到体积增长的上下界估计时也有很多重要的结果。在没有曲率假设条件的情况下,利用势函数的上下界估计,曹怀东和周德堂 [29] 得到了一个经典的体积增长的上界估计:
定理3.3:令
为一个完备非紧致的梯度收缩Ricci孤立子,存在常数
使得当
且充分大时有:
对于Gaussian孤立子,上述估计结果估计形式为其最优估计。在没有任何需要曲率假设条件的情形下,Munteanu [30] 证明了满足
的标准化条件的完备非紧致梯度收缩Ricci孤立子,存在常数
及
使得对于任意
,有
。
基于 [28] 中命题2.1的证明,Zhang [31] 也得到了一个体积增长的上界估计:
推论3.4:令
为一个完备非紧致的梯度收缩Ricci孤立子,设
,则对任意
,存在仅取决于
的常数
使得对于任意
,体积上界增长满足:
同上述推论假设条件,完备非紧致的梯度收缩Ricci孤立子,给定
,存在取决于
及
的常数
使得对于任意
,有
。进一步,对任意
,存在取决于
及
的常数
,
,当
时有
。
若势函数在球面方向上满足一定的均匀条件,则梯度稳定Ricci孤立子有至多欧氏体积增长 [32]:
推论3.5:令
为一个完备梯度收缩Ricci孤立子,且
。设存在常数
使得
,
充分大,则对任意
,存在
,任意
,有:
此外该孤立子有至多欧式体积增长,即对任意
,存在
,任意
,有:
若对于充分大的
有
,则有
推论3.6:令
为一个完备非紧致的梯度收缩Ricci孤立子,且满足标准化条件
。则存在常数
,使得当
,
时有:
推论3.7:令
为一个完备非紧致的梯度收缩Ricci孤立子,平均曲率满足
,其中常数
且
充分大。则存在常数
,使得:
利用Carillo-Ni [28] 对数形式的Sobolev不等式及Perelman的非坍塌理论,Cao [33] 还得到了一个体积增长对数形式的下界估计。
定理3.8:令
为一个完备非紧致的梯度收缩Ricci孤立子,则
有无穷大的体积。准确地说,即存在常数
,使得
充分大时有:
基于Perelman [2] 的方法及对数形式的Sobolev不等式,在不需要额外的曲率条件假设时,Munteanu-Wang [34] 证明了一个体积增长的下界的线性估计结果:
推论3.9:令
为一个完备非紧致的梯度收缩Ricci孤立子,则存在仅取决于维数
及Perelman不变量
的常数
,使得任意时
,有:
其中
为
的最小值点且
仅取决于维数
。
由对数形式的Sobolev不等式,显然任意具有有界Ricci曲率的完备非紧致梯度收缩Ricci孤立子有至少线性体积增长 [35]:
定理3.10:令
为一个完备非紧致的梯度收缩Ricci孤立子
,若存在
使得
,其中
为一个非零常数,
表示距离函数
,
为一个非负常数。则当
充分大时,有:
特别地,
时,有
;
时,有
。
对于梯度扩张Ricci孤立子,Chen [36] 也得到了类似的上界估计:
推论3.11:令
为一个数量曲率为
的完备非紧致梯度扩张Ricci孤立子,若存在
使得
,常数
,则对
,常数
充分大,有:
此外,
且
时,
。
定理3.12:令
为完备非紧致的梯度扩张Ricci孤立子,若
,(
)。则对任意
及
,有:
且对任意
及
,有:
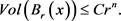
此外,若其渐近体积比存在,则对任意
及
,有
。
对于稳定Ricci孤立子,Menteanu-Sesum [26] 也证明了类似于收缩孤立子(推论3.10)的线性增长结果:
定理3.13:令
为任意梯度稳定Ricci孤立子,则存在常数
,对任意
,其体积增长满足:
由于Bakry-Emery Ricci张量
及其他曲率条件的引进,势函数的估计出现许多新的证明方法及更精确的结果,结合势函数估计结果及势函数水平集的几何性质,Ricci孤立子的体积估计将会有更完善的结果。
基金项目
本文由山东省自然科学基金(ZR2018MA006)及山东省研究生导师指导能力提升项目(SDYY17009)支持。
NOTES
*通讯作者。