1. 引言
随着地理空间信息技术和卫星遥感等数据采集器的越发先进,空间数据的数量和质量呈海量增长。如何有效从空间数据中发掘、检测出有效的信息和知识已经成为了当前研究的重要方向。将数据挖掘技术应用到空间数据中,即空间数据挖掘,是解决当前问题的重要手段。空间数据挖掘主要功能包括关联分析、聚类分析、组合分析、离群检测等方面。
其中空间数据的离群检测作为空间数据挖掘研究的重要前提和方法,是空间数据挖掘不可或缺的部分,目前已经广泛应用在地质灾害监测、成矿预测、环境监测、矿山水文检测、疾病控制和监测 [1] 等众多领域。
空间数据是用来描述现实世界中的事物的大小、位置、轮廓、属性等信息的数据,空间数据相比于普通数据具有的特性是空间自相关性和异质性。因此普通的离群点检测方法不适用于空间数据的离群点检测,需要充分考虑空间数据的特性,才能有效的检测出空间异常点。
最早的空间数据离群检测是由地学统计学发展而来,主要分为空间数据可视化和属性定标两种方法,其中空间数据可视化方法主要有变差云图 [2] ,qqplot图 [3] 等方法,而属性定量的方法主要包括Moran散点图 [4] 、Z-Value法等方法 [5] 。
Shekhar等人从空间数据的本质出发,首次提出了二分法(SLZ) [6] ,将空间数据分为空间属性和非空间属性,根据空间属性确定空间对象的空间邻域,通过计算非空间属性确定空间对象邻域内的差异,计算离群因子。但是SLZ算法使用的是全局的阈值,求出的是全局的空间离群点。
对于多维非空间属性的处理,文俊浩 [7] 等人提出使用马氏距离计算各个维度非空间属性的差异。但是马氏距离并不能有效的表示数据的自相关性。Sun等人在SLZ的算法中加入波动参数提出了SlOM算法 [8] ,国内薛安荣等人提出了普适的SLOF算法 [9] ,并针对混合类型的非空间属性提出了相关算法。张忠平等人提出了基于KNN图 [10] 的空间离群检测算法,利用KNN图来构建空间邻域,KNN图的时间复杂度较高,不适用于海量数据。综合上诉算法可以发现存在两个问题:在空间邻域的构建方面,算法大多时间复杂度过高,不适合处理空间高维数据,人为影响较大;在非空间属性的度量方面,对空间数据的研究不够深入,离群因子的定义存在误差。
本文针对上述算法在空间邻域的构建方面存在的问题,引入Delaunay三角剖分的思想,通过Delaunay三角剖分来构建空间数据的空间邻域,利用空间。并结合某矿山钻孔数据进行实验,最终依据实验结果,从算法的检测率、时间复杂度、算法鲁棒性等方面对该算法的性能进行分析。
2. 基于Delaunay三角剖分的空间离群检测算法
本文提出的基于Delaunay三角剖分的空间离群检测算法的具体思路如下:首先根据
准则,选取各个维度的全局离群点,再依据Delauanay三角剖分生成空间邻域,然后将数据预处理中选取的离群点的值用改点邻域内对象的均值代替,建立相应的空间权重矩阵,在确定的空间权重矩阵下,依据SLOF离群因子的计算方法,度量空间邻域内的差异,选取SLOF离群因子前n个大的值作为离群点输出。
具体的算法流程如图1所示:
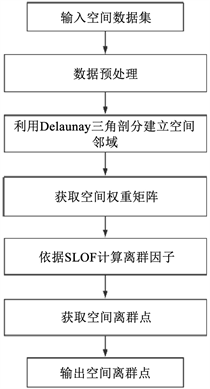
Figure 1. Spatial outlier detection algorithm based on Delaunay triangulation
图1. 基于Delaunay三角剖分的空间离群检测算法
2.1. 相关定义
存在空间对象集
,由n个对象组成,其中
表示对象间在p条件下相连接,对于对象s
,
表示空间属性,
表示非空间属性。
定义1:(空间邻居)当对象
和
符合条件
,那么
就是
的空间邻居。
定义2:(空间邻域)空间对象
所有的空间邻居的集合称为
的空间邻域。
定义3:(
准则)计算数据集的分布误差,将数值分布在
的点设定为全局离群点。
定义4:(Delaunay三角剖分)对空间数据进行三角网划分,其中当划分成的三角网满足以下两个特性,a:空球准则,单个三角形或不规则的四面体的外接圆或外接球内部不包含除顶点外的其它点。b:最大-最小角准则每个三角的角度都满足是所有可能三角形中最小的。
定义5:(空间权重)对象
和对象
是空间邻居,那么选取反距离公式
为空间权重,dist表示对象间的距离,当对象
和
不满足空间邻居关系时,那么W的值为0。
定义6:(邻居加权距离) dist (
)表示对象与对象间的邻域距离如公式2所示,Wk表示是第k维度的权值,
表示
对象的在k维的权重。
(公式2.1)
定义7:(邻域距离)
表示表示对象所有空间邻域内的邻域距离,其中
表示邻域内所有对象的数量。
(公式2.2)
定义8:(离群因子)存在数学公式能够计量对象在空间邻域内的非空间属性的差异,该数学公式可以认为是是离群因子。
定义9:(SLOF离群因子) SLOF的离群因子定义公式如下,选择SLOF值最大的前n个点作为空间离群点。
(公式2.3)
2.2. 数据预处理
将获取的数据集,进行数据格式转换,整合操作,空间异常点会影响到局部离群因子的度量,根据定义3,鉴别出空间数据集中的全局离群点,并将其保存。
2.3. 通过Delaunay三角剖分构建空间邻域
传统的空间邻域构建方法存在参数选择困难,构建时间复杂度过高,人为因素较大等问题。而基于Delaunay的三角剖分算法,常见的实现方法有逐点法,三角网增长法等,这些算法的时间复杂度最优能达到
,Delaunay三角剖分本身具有严格的数据验证和坚实的理论基础。具有能有效维护空间数据的拓扑信息,便于三维分析和显示等良好的几何特性。
2.4. 建立空间权重矩阵
根据生成的空间邻域,建立相应的空间邻域矩阵,表1表示生成的相应的空间对象邻域表。

Table 1. Generating spatial neighborhood table based on Delaunay triangulation
表1. 基于Delaunay三角剖分生成空间邻域表
结合表1和定义5建立空间权重矩阵。示例给定简单空间数据集,生成Delaunay剖分四面体如图2(a)所示,p1~p5表示空间对象,图2(b)为生成的相应空间权重矩阵。
2.5. 空间邻域离群因子的度量
依据定义8中的SLOF算法的离群因子的计算复方式,结合上文生成的空间邻域矩阵,生成空间离群因子,其中空间权重选取反距离权重公式进行计算,为了防止SLOF的值为0,将公式2.3改为公式2.4所示:
(公式2.4)
一般取值为1 * 10−6左右,当SLOF的值大于1时,离群程度开始变高,当小于1时,表示离群程度正常。最终选取SLOF值前n个大的点作为空间离群点。
 (a) 空间对象示意
(a) 空间对象示意 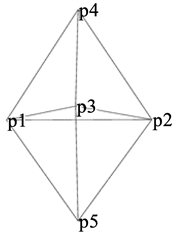 (b) 基于Delaunay三角剖分生成的空间权重矩阵
(b) 基于Delaunay三角剖分生成的空间权重矩阵
Figure 2. Schematic diagram of spatial weight matrix
图2. 空间权重矩阵示意图
2.6. 算法的描述与复杂度分析
基于Delaunay三角剖分的空间离群检测算法(数据包含N个对象)
输入:空间数据集
输出:空间离群点
Step 1:对空间数据集进行预处理,甄选出全局离群点,需要求取数据集合的均值方差等,时间复杂度为
。
Step 2:建立空间邻域,通过Delaunay三角剖分对空间数据集进行处理,建立空间邻域,时间复杂度为
Step 3:计算空间权重矩阵,利用Delaunay三角剖分生成的空间邻域,将全局离群点灯值用邻域均值代替,最后建立空间权重矩阵,时间复杂度为
。
Step 4:计算空间邻域内的空间离群因子,结合SLOF算法,根据生成的空间邻域矩阵生成空间离群因子,时间复杂度为
。
综上所诉本文时间复杂度为
。
3. 实验和分析
本文算法结合某地区稀土矿区具体钻孔数据,使用k邻域图法和本文所提算法做具体实验对比。实验环境为win10操作系统,采用MATLAB2017b和C语言编程。
3.1. 算法实验
结合某地矿区的钻孔的数据集对算法进行分析,其中X,Y,Z表示空间坐标,非空间属性为各个采样点的品味,共有240个值。
通过
准则没有发现全局离群点,使用k邻域图法和Delaunay三角剖分建立空间邻域,根据生成的空间邻域结合SLOF离群因子定义,计算相应的空间离群点。
其中图3(a)表示矿山某钻孔具体采样散点图如图3(b)根据Delaunay生成的空间邻域算法的时间复杂度度对比如图4所示。
 (a) 钻孔采样点散点图
(a) 钻孔采样点散点图  (b) 空间邻域示意图
(b) 空间邻域示意图
Figure 3. Scatter diagram and spatial neighborhood diagram of borehole sampling points
图3. 钻孔采样点散点图和空间邻域示意图
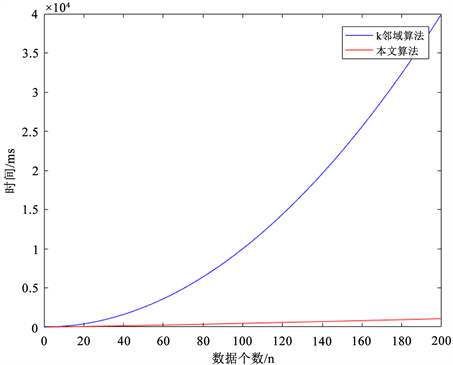
Figure 4. Comparison of time complexity between the two algorithms
图4. 两种算法时间复杂度对比
3.2. 实验结果分析
表2为Delaunay三角剖分检测出的离群点,表3为K邻域法检测出的离群点。
1) 从检测精度对两种方法进行分析:结合现场采集数据具体情况,可以发现基于Delaunay三角剖分方法检测出的离群点,其检测精度达到80%,而k邻域的方法,其检测精度仅在k值为5时,最高达到80%,因此可以得出本文所提算法的检测精度高于k邻域方法。

Table 2. Outliers detected from Delaunay triangulation
表2. 基于Delaunay三角剖分检测出的离群点

Table 3. SLOF algorithm detects different k values
表3. SLOF算法不同k值检测结果
2) 从人为因素进行分析:k邻域的算法,在k值选取方面存在人为因素,最优k值难以选择。而本文算法,完全基于Delaunay三角剖分建立空间邻域,无需对k值进行设定和检测。
3) 从算法时间复杂度进行分析:如图4所示,当数据量增长较快时,本文算法时间复杂度增长较为缓慢,而k邻域算法时间复杂度增长呈指数增长,因此可得本文算法在时间复杂度方面优于k邻域算法。
4. 结束语
传统的基于KNN邻域图的空间离群检测算法,在空间邻域构建方面,存在算法时间复杂度过高,最优k值受人为因素影响大等不足,而Delaunay三角剖分对空间数据在空间邻域构建方面具有优势,算法本身也较为成熟,背后也具有深厚的数学理论基础。因此本文引入Delaunay三角剖分的方法,构建空间数据的空间邻域,并结合SLOF算法中对空间邻域离群因子的计算方法,求出空间数据的离群点。但是空间数据往往不是单个点存在,可能是多个点、线、面组成的,空间数据的非空间属性大多也是多维的。为此下一步将研究多维属性的复杂空间数据的空间离群点检测算法。