关于未定元的注记

A Note on the Indeterminate

摘要: 设D是一个整环，Q是其商域，本文证明了x是D上的未定元，当且仅当x是Q上的未定元。

Abstract: Let D be an integral domain and Q be its field of fractions. It is proved in this note that x is an inde-terminate over D if and only if so is x over Q.

1. 引言

本文所使用的符号和术语都是标准的，可参考 [1] [2] 与 [3] [4] 。

假定 $R_0$ 是一个具有单位元的交换环， $R$ 是 $R_0$ 的子环并且包含 $R_0$ 的单位元。设 $\alpha \in R_0$ ，一个可以写成

$a_0+a_1\alpha +\cdots +a_n{\alpha }^n\left(a_i\in R,i=0,1,2,\cdots ,n\right)$

形式的的元称作 $R$ 上的 $\alpha$ 的多项式，其中 $a_i$ 称为多项式的系数。

$R_0$ 的一个元 $x$ 称作 $R$ 上的一个未定元，如果在 $R$ 里找不到不全为零的元 $a_0,a_1,\cdots ,a_n$ 使得

$a_0+a_{1}x+\cdots +a_n{x}^n=0$

令 $b_0+b_{1}x+\cdots +b_n{x}^n$ 是环 $R$ 上一个一元多项式，则非负整数 $n$ 称为这个多项式的次数。特别地，多项式0没有次数。

值得注意的是， $R_0$ 中未必存在 $R$ 上的未定元。例如，有理数集合中就不存在整数集合上的未定元。不过，却有如下的结论：

给定具有单位元的交换环 $R$ ，必存在 $R$ 上的未定元，而也就有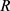上的多项式环 $R\left[x\right]$ 存在。

在本文中，关于未定元的刻画，我们有下面的结论。

命题1：设D是一个整环，Q是D的一个商域，则 $x$ 是D上的一个未定元，当且仅当 $x$ 是Q上的未定元。

2. 证明

为命题的证明，我们需要下面的几个引理，其中引理1与引理3分别是[3，第三章第十节定理1]和[3，第三章第十节定理3]。

引理1：无零因子的交换环 $R$ 必是一个域 $F$ 的子环，其中 $F$ 刚好是由所有元

$\frac{a}{b}\left(a,b\in R,b\ne 0\right)$

所做成的，其中

$\frac{a}{b}=a{b}^{-1}=b^{-1}a$ 。

引理2：若 $R$ 是一个整环，则 $R$ 上的一元多项式环 $R\left[x\right]$ 也是一个整环。

证明：注意到， $R\left[x\right]$ 是一个有单位元的交换环。要证 $R\left[x\right]$ 是一个整环，只需证明 $R\left[x\right]$ 是没有零因子。

设 $f\left(x\right),g\left(x\right)\in R\left[x\right],f\left(x\right)\ne 0,g\left(x\right)\ne 0$ ，那么 $f\left(x\right)$ 和 $g\left(x\right)$ 可写成

$f\left(x\right)=a_0+a_{1}x+\cdots +a_m{x}^m\left(a_i\in R,i=1,2,\cdots ,m\right)$

$g\left(x\right)=b_0+b_{1}x+\cdots +b_n{x}^n\left(b_j\in R,j=1,2,\cdots ,n\right)$

的形式，这里 $a_m\ne 0,b_n\ne 0$ 。于是

$f\left(x\right)g\left(x\right)=c_0+c_{1}x+\cdots +c_{m+n}{x}^{m+n}\left(c_k\in R,k=1,2,\cdots ,m+n\right)$ 。

但 $a_m,b_n\in R$ ，而 $R$ 无零因子，所以 $c_{m+n}=a_m{b}_n\ne 0$ ，从而 $f\left(x\right)g\left(x\right)\ne 0$ 。因此， $R\left[x\right]$ 无零因子。

引理3：若 $R$ 是一个至少含两个元素的环， $F$ 是一个包含 $R$ 的域，则 $F$ 包含 $R$ 的一个商域。

命题的证明：若 $x$ 为Q上的一个未定元，则由D $\subset$ Q可知 $x$ 也是D上的未定元。

设 $x$ 为D上的未定元，由Q是D的商域可知 $x\notin Q$ ，下证 $x$ 也是Q上的未定元。因 $x$ 为D上的未定元，所以存在一元多项式环 $D\left[x\right]$ 。由引理2，可知 $D\left[x\right]$ 也为整环。从而，存在域F使得 $D\left[x\right]$ 成为F的子环。注意到，D $\subset$ F。由引理3，Q $\subset$ F。

在F中考虑运算，假设有Q中不全为零的元 $\frac{c_0}{b_0},\frac{c_1}{b_1},\cdots ,\frac{c_n}{b_n}$ ，其中 $c_0,c_1,\cdots ,c_n\in D$ 不全为零， $b_0,b_1,\cdots ,b_n\in \text{D}$ 均不为零，使得

$\frac{c_0}{b_0}+\frac{c_1}{b_1}x+\cdots +\frac{c_n}{b_n}{x}^n=0$ 。

于是，

$\frac{1}{b_0{b}_1\cdots b_n}\left(c_0{b}_1\cdots b_n+c_1{b}_0{b}_2\cdots b_{n}x+\cdots +c_n{b}_0{b}_1\cdots b_{n-1}{x}^n\right)=0$ 。

故

$c_0{b}_1\cdots b_n+c_1{b}_0{b}_2\cdots b_{n}x+\cdots +c_n{b}_0{b}_1\cdots b_{n-1}{x}^n=0$ 。

由于 $x$ 为D上的未定元，所以，

$c_0{b}_1\cdots b_n=0,c_1{b}_0{b}_2\cdots b_n=0,\cdots ,c_n{b}_0{b}_1\cdots b_{n-1}=0$

又D无零因子，故 $c_0,c_1,\cdots ,c_n$ 均为零，矛盾。

致谢

作者感谢河南工业大学理学院科教融合项目以及河南工业大学“大学生创新创业训练计划项目”的支持。作者同时感谢审稿人的宝贵意见。

基金项目

本文由河南工业大学项目(26510009)、河南省教育厅项目(17A110004)以及科技厅项目(182102410049)资助。

NOTES

^*通讯作者。