1. 前言
本文提到的空间均为
空间,用
表示正整数集。空间X上的实值函数f称为下半连续(上半连续) [1] ,如果对任意实数
,集合
为开集。记
为X到闭区间[0, 1]上所有下半连续(上半连续)函数的集合。
设X为拓扑空间,用
表示X上的拓扑,
为X的所有闭集构成的集族,
表示X的所有紧集的集族。设
,记
为A的特征函数。
设f为半连续函数,在什么条件下存在连续函数列
使得这一
问题称为实值函数的函数列逼近问题。Tong在文献 [2] 证明了空间X是完备正规当且仅当对X上的任意下半连续函数f,存在X上的递增连续函数列
使得
。张国芳在文献 [3] 证明了空间X是k-半层空间当且仅当对每一
,存在递增函数列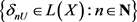 满足
;若
且
,则对每一
,
;对每一紧集
,U为开集且
,则存在
使得对任意
有
。完备正规空间,k-半层空间均为具有闭-
性质的空间,由于具有紧-
性质的空间与具有闭-
性质的空间在结构上相似,一个自然的问题是具有紧-
性质的空间是否也有类似的函数刻画。给出某些具有紧- Gδ 性质空间如
-空间、c-层空间、kc-半层空间的函数刻画。
满足
;若
且
,则对每一
,
;对每一紧集
,U为开集且
,则存在
使得对任意
有
。完备正规空间,k-半层空间均为具有闭-
性质的空间,由于具有紧-
性质的空间与具有闭-
性质的空间在结构上相似,一个自然的问题是具有紧-
性质的空间是否也有类似的函数刻画。给出某些具有紧- Gδ 性质空间如
-空间、c-层空间、kc-半层空间的函数刻画。
设X为拓扑空间,若映射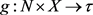 ,满足:对每一
及
,
;
;则称g为X上的一个g-函数。对于一个子集
,
。
,满足:对每一
及
,
;
;则称g为X上的一个g-函数。对于一个子集
,
。
定义1.1 [4] :空间X称为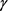 -空间。若存在X上的g-函数g,使得若对每一
,
且
,则
为
的聚点。
-空间。若存在X上的g-函数g,使得若对每一
,
且
,则
为
的聚点。
定义1.2 [5] :空间X称为c-半层空间(c-层空间)。若存在X上的g-函数g,使得对每一
,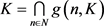 (
)。
(
)。
定义1.3 [6] :空间X称为kc-半层空间。若存在g-函数g,使得对任意
且
,则存在
使得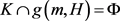 。
。
2. 主要结果
本节中,我们将利用实值函数给出
-空间,c-层空间,kc-半层空间的若干等价刻画。
引理2.1 [7] :X为
-空间当且仅当存在X上的g-函数g使得若
,
且
,则存在
使得
。
定理2.2:X为
-空间当且仅当对每一
,存在递减函数列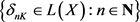 满足
满足
(1)
;
(2) 若
且
,则对每一
,
;
(3) 对每一紧集
及
且
,存在
使得对任意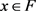 有
。
有
。
证:设
为
-空间,g为引理2.1中的g-函数,对每一
及
,令
,则
关于n递减且
。
(1) 设
,对每一
,若
,则对每一
,
,于是
;若
,则存在
使得
,于是当
时,有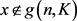 ,故
。
,故
。
(2) 设
且
,则对每一
,有
,由此可得
。
(3) 设
,
且
,由引理2.1,存在
使得 ,故对任意
,有
,则
。
,故对任意
,有
,则
。
反之,对每一
及
,令
。由(1),对每一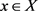 ,有
,故存在
使得对任意
,
。由于
关于n递减,故对每一
,
,则
。显然对每一
及
,有
,故g为X上的g-函数。
,有
,故存在
使得对任意
,
。由于
关于n递减,故对每一
,
,则
。显然对每一
及
,有
,故g为X上的g-函数。
对每一
及
,令
。设
,则存在
使得
,则
,由条件(2)得
,故
,这表明
。设
,
且 K ∩ H = Φ ,由条件(3),存在
使得对任意
有
,故
,从而
。由引理2.1,
为
-空间。
定理2.3:X为
-空间当且仅当对每一
,存在递减函数列
满足:
(1) 对每一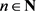 及
,若
,则
;
及
,若
,则
;
(2) 若
且
,则对每一
,有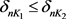 ;
;
(3) 若
,
且
,则
在
上一致收敛于0。
证:设
为
-空间,g为引理2.1中的g-函数,对每一
及
,令
则
关于
递减且
。(1),(2)显然成立。
(3)设
,
且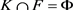 ,由引理2.1,存在
使得
。对
,当
时,对任意
有
,故
,这说明
在
上一致收敛于0。
,由引理2.1,存在
使得
。对
,当
时,对任意
有
,故
,这说明
在
上一致收敛于0。
反之,对每一
及
,令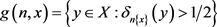 。由(1)知,每一
及
,
,又
,故g为X上的g-函数。对每一
及
,令
,由定理2.2的充分性的证明知
。设
,
。由(1)知,每一
及
,
,又
,故g为X上的g-函数。对每一
及
,令
,由定理2.2的充分性的证明知
。设
,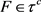 且
,由条件(3),
在
上一致收敛于0,则存在
,对任意
,有
,于是
,故
,则X为
-空间。
且
,由条件(3),
在
上一致收敛于0,则存在
,对任意
,有
,于是
,故
,则X为
-空间。
定理2.4:X为正则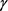 -空间当且仅当对每一
,存在递减函数列
-空间当且仅当对每一
,存在递减函数列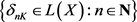 ,满足:
,满足:
(1)
;
(2) 若
且若
,则对每一
,有
;
(3) 若
,
且
,则存在开集
及
使得对任意
有
。
证:设
为
-空间,g为引理2.1中的g-函数,对每一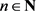 及
及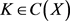 ,令
,则
关于
递减且 δnk ∈L (X) 。(1) (2)的证明同定理2.2。设
,
且
,由于
为正则空间,故X的无交开集U,V使得
,存在
使得
,则
,故对任意一
,有
。
,令
,则
关于
递减且 δnk ∈L (X) 。(1) (2)的证明同定理2.2。设
,
且
,由于
为正则空间,故X的无交开集U,V使得
,存在
使得
,则
,故对任意一
,有
。
反之,由定理2.2知X为
-空间,下证
为正则空间。对每一
及
,令
。设
,由(3)得,存在开集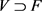 及
使得对任意
,
,则
,故
及
使得对任意
,
,则
,故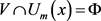 ,这说明
为正则空间。
,这说明
为正则空间。
定理2.5:X为c-层空间当且仅当对每一
,存在递减函数列
及
满足:
(1)
;
(2) 若
且
,则对每一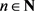 ,
;
,
;
(3) 对每一
及
,
。
证:设
为X的c-层函数,对每一
及
,令
,
,则
关于n递减且
。(2) (3)显然成立。
(1) 设
,若
,则
,则对每一
,有
,则
;若
,则
,故存在
使得对任意
,有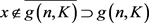 ,于是
。
,于是
。
反之,对每一
及
,令
,则g为X上的g-函数。对每一
及
,令
,则
。设
,则存在
使得
。由条件(2),(3)得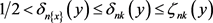 ,故
,这表明
,故
。
,故
,这表明
,故
。
设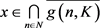 ,则对每一
,
,则
,故
,则对每一
,
,则
,故
,这说明
,于是
。故
为c-层空间。
定理2.6:X为kc-半层空间当且仅当对每一 K ∈C(x) ,存在递减函数列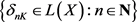 满足
满足
(1) 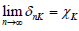 ;
;
(2) 若
且
,则对每一
,有
;
(3)若
且
,则存在
使得对任意
有
。
证:设g为kc-半层函数,对每一
及
,令
,则
关于
递减且
。(1) (2)的证明同定理2.2。设
且
,则存在
使得
,故对任意
,
。
反之,对每一
及
,令
,则g为X上的g-函数。对每一
及
,令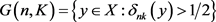 ,则
。设
且
,由条件(3),存在
使得对任意
,则
。设
且
,由条件(3),存在
使得对任意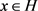 有
,故
,从而
。故
为kc-半层空间。
有
,故
,从而
。故
为kc-半层空间。
由定理2.2的证明可得:
定理2.7:X为kc-半层空间当且仅当对每一
,存在递减函数列
满足
(1) 对每一
及
,若
,则
;
(2) 若
且
,则对每一
,有
;
(3) 若
,且
,则
在
上一致收敛于0。
由定理2.5的证明可得:
命题2.8:X为c-半层空间当且仅当对每一 K ∈C(x),存在递减函数列
满足
(1)
;
(2) 若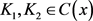 且
,则对每一
,有
。
且
,则对每一
,有
。
参考文献