1. 引言
研究临界点的方法,主要是通过非线性规划、构造特征变量等手段与方法。在一部分求解临界点的问题中,将临界点问题转换为计算有约束条件的非线性规划的最优解,并利用牛顿法、罚函数法等方法求出临界点。而另外一部分求解临界点的问题中,则是通过研究系统本身的性质,构造其独特的特征统计量,以其统计量的突破以判定其为临界点。
研究表明 [1] [2] [3] [4] ,许多复杂疾病存在临界点。在疾病发生前疾病可能会潜伏数年,但发生异变却只仅仅在疾病爆发前几个月时间内。换言之,在疾病爆发前存在一个疾病过渡的时期,在该时期中,生物系统从健康状态过渡到疾病发生状态。而疾病过渡期就是我们所需要探寻的复杂疾病临界点。探测复杂疾病临界点至关重要,一方面对疾病的早期治疗有极大的帮助 [5] ,另外一方面,通过针对临界点时的研究也进一步促进对疾病发生机理的了解 [6] [7] 。
疾病的发展过程一般可以分为三个过程:1) 健康状态。在该状态下系统对扰动具有较强的鲁棒性与回复能力。2) 疾病过渡期。该状态是发生相变之前的临界状态,该状态下系统表现为对扰动非常敏感、回复能力弱。3) 疾病爆发期。在该状态下系统表现为对扰动又具有强鲁棒性与回复能力。现有研究表明,对比健康状态与疾病过渡期的患者,尽管在一些静态特征上并无显著性差异,但一些动态特征则存在显著性差异,具体为:1) 影响疾病动态网络标志物基因之间相关性提高。2) 动态网络标志物基因与其他基因之间相关性减少。3) 动态网络标志物基因的标准差大幅增加 [2] 。
本文结合差异化网络的方法与隐马尔科夫模型,以疾病发展过程的三个过程作为隐马尔科夫模型的隐藏状态,以构造个体差异化网络后与参考基因网络的皮尔逊相关系数差值作为观测序列,将之前所有时刻数据为训练样本,训练当前模型,再根据当前模型计算得到下一时刻进入疾病过渡期的概率,并以此作为探测临界点的基本指标。通过结合构建个体差异化网络的方法后,探测临界点时对所需要的实验样本数量更少。
为了检验方法有效性,将该方法用到九个节点的模拟数据集、肺部急性损伤数据(GSE2565)、前列腺癌数据(GSE5345)当中,均成功在其疾病爆发期之前探测到其临界点,动态网络标志物基因在临界点转为高表达,在其临界点前后基因表达发生较大的翻转。另外,对指标产生较明显影响的基因分别进行功能分析与生存,通过功能分析可以得到,这些基因均来自一些对疾病有直接关系的通路,同时这些有明显影响的基因通过生存分析看到对前列腺患者的存活率有显著影响,上述结果均说明方法稳定可靠。
2. 方法
2.1. 单样本个性化网络
传统探测临界点方法均利用多个实验样本以提供多组实验基因,继而能够计算实验组中基因与基因之间相关性,探测的是一个普遍性临界点。而2016年有研究提出了构建基于个人特异性的网络方法 [8] 。其个人特异性网络的构建方法(图1(A)):
取出N个正常人的样本,不妨假设其中与探测疾病可能相关的基因对共有m对,计算每对基因之间的皮尔逊相关系数(Pearson Correlation Coefficient,下文均用PCC代替),得到m个PCC值,不妨按一定顺序命名为
。
将特定个人(实验样本)的基因组加入N个正常人样本中,即共N + 1个样本,这时重新计算每两个基因之间的PCC,不妨记为
。计算
。
每一对基因之间的均可计算∆PCC,这就组成了单样本的个性化网络,并且当n较大时,∆PCC符合以下分布:
,
(1)
通过z检验之后,得到z值:
(2)
那么此时
符合正态分布。
但实际上生物数据中通常样本量极少,所以z并非正态分布,而∆PCC是服从火山分布 [8] ,而该种分布只知道与n相关,无法写出表达式。
2.2. 隐马尔科夫模型
其正常无差异的基因对的∆PCC应服从“火山分布”。“火山分布”在n较大时,根据文章中的测试:n > 50能够通过Kolmogorov-Smirnov测试,以证明火山分布与标准正态分布是相似的。但其在n较小时,并无一个表达式或是一个相似的分布,而只能确定其与n相关。而在n较小时,利用z-test或是t-test进行显著性检验,显然也是不合理的。
但在确定n之后,在同一的状态下,其∆PCC是符合一定的分布。但当状态发生改变时,根据复杂疾病临界点的理论,在同一组中的基因对的PCC变为趋于1,为组内基因与组外基因的PCC则变为趋于0。换一句话说,当状态从疾病发生前转变到疾病过渡期时,与疾病相关的基因对的PCC值与正常状态下的PCC值发生显著性变化,其∆PCC不再服从上一时刻中的分布。故利用隐马尔科夫模型,即可通过训练得到疾病发生前的∆PCC的分布,进而计算下一个时刻已知观测情况下,其为疾病发生前、疾病过渡期的概率。
我们将疾病发生前、疾病过渡期、疾病爆发期作为隐马尔科夫模型中无法直接观测到的三个状态,但由于我们研究的仅仅是探测疾病过渡期,故实际仅考虑疾病发生前、疾病过渡期,隐马尔科夫模型变量设定如表1。


Table 1. Variable setting of hidden Markov model
表1. 隐马尔科夫模型变量设定
那么,当我们探测临界点T时,T满足以下条件:(1) T − 1时刻为状态
,(2) T时刻进入到状态
。即求得T,使得t = T时,公式(3)达到最大
(3)
研究中,由于不考虑状态w3的情况,并且三种状态是有序发生的,所以有
(4)
由于t时刻的状态跳转仅与t − 1时刻状态有关,所以(4)可以写为:
(5)
并以此判定t时刻是否是临界点T,记I(t)为个体特异性异常指标,当指标越大,则说明此时样本发生状态跳转的可能性越大,反之则为样本发生状态跳转的可能性越小。结合复杂疾病临界点理论,则该指标在疾病过渡期会发生突增。
2.3. 算法设计
步骤一:取
个正常人样本,计算与疾病相关的所有基因对之间的PCC,记为
,
,其中m是相关基因对数量。
步骤二:记实验样本总数为
,对每一个实验样本分别进行以下操作:结合
个正常人样本,形成共
个样本,对时间T − 1以前的所有基因对,求其PCC,并计算
,其中
。记对照组样本数共
,对所有对照样本做相同的处理,得
,
,并对各个
进行分组。
步骤三:以T − 1时刻以前的这些基因对(不分对照组或实验组)作为训练样本,以其
,
作为观测序列,并认为这些样本均处于
状态。得到T − 1时刻的隐马尔科夫模型
(图1(B))。
步骤四:对第j个实验样本,
,分别进行以下操作:用训练得到的
,计算实验组在T时刻观测序列为
不一致性指标:
(6)
另一方面,对对照组实验样本j2,
,计算对照组在T时刻观测序列
下的不一致性指标:
(7)
步骤五:计算
,以此作为个体特异性异常指标。如果
发生急剧上升的话,则认为T为临界点。否则进入下一个时间点,回到步骤二。其每一个时间点所有样本的
或
做成箱型图,将个体特异性异常指标连接得到图1(C)。
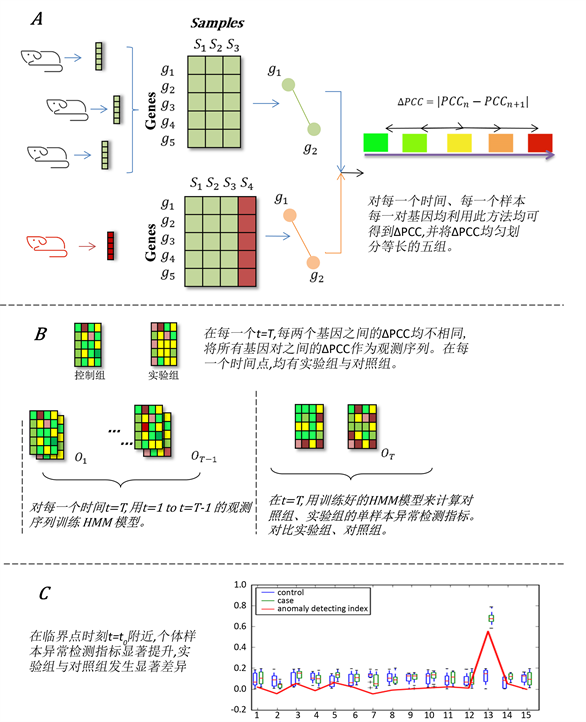
Figure 1. Using hidden Markov model to construct individual-specific anomaly index to detect complex disease network critical point
图1. 利用隐马尔科夫模型构建个体特异性异常指标并探测临界点方法概述
3. 主要结果
3.1. 探测9节点模拟数据临界点
该部分本文通过构造9节点基因调控网络,生成疾病仿真数据,并将本文中算法应用在模拟数据中探测疾病临界点。
复杂疾病发展过程的动态过程无论在恶化前或者是恶化后都是非常复杂的,由于复杂疾病有超过数千个因素影响(如基因因素、遗传因素等),因此状态方程通常具有大量变量与参数。但过去研究表示 [9] [10] [11] [12] ,可以将复杂疾病动态过程简化为:
(8)
其中,
代表在第k个时间点的n维基因状态,同时也是基因或蛋白质浓度,
是s维参数向量,也代表多个疾病状态影响因素。若系统同时满足以下条件:
1)
是系统(8)的平衡点,即
。
2) 存在一个
使得雅各比矩阵
存在一个特征值,该特征值或其复共轭对的模等于1。
3) 当
时,J的特征值的模均不等于1。
那么当q达到
时,系统在
产生分岔。
根据以上特征,本文利用以Michaelis-Menten方程结合基因自身的降解速率,构建出9个节点的基因调控网络,公式(9)中9个微分方程体现了节点之间调控关系,其基因网络如图2(A)所示。
(9)
在公式(9)中,参数Q是标量控制变量,
是均值为0的高斯噪音。
代表mRNA-i浓度。其稳定平衡点为
(10)
并且可以将微分方程转变为
的形式。
我们设
的雅各比矩阵为
,这里
(11)
A为公式(9)的系数矩阵。令
,从J中我们可以得到9个互不相同的特征值
。当 时,
,此方程在该点为一个分岔点,即当
时,平衡点
是稳定,当Q从小于0接近
时,系统变得不稳定,即
为该微分方程一个分岔点。
时,
,此方程在该点为一个分岔点,即当
时,平衡点
是稳定,当Q从小于0接近
时,系统变得不稳定,即
为该微分方程一个分岔点。
将本文方法应用于上述构造的模拟数据集中,其个体特异性异常指标如图2(B)所示,当参数接近Q = 0的时候,个体特异性异常指标剧烈的增长,而在当Q远离0点时,指标接近于0。另外,在Q = 0的时,实验样本的指标所形成的“箱体”变大,即趋于不稳定。

Figure 2. Simulated data set network architecture (A) and verification results (B)
图2. 模拟数据集网络结构(A)与验证结果(B)
值得注意的是,虽然模拟数据集中已知基因连接结构,但使用本文方法时并未使用其网络结构,即探测临界点时不再需要知道原基因之间的连接结构,仅仅需要把可能相关的基因多个时间节点的值放入模型当中即可。
3.2. 探测实际数据集的临界点
将该种方法应用于肺癌数据(GSE2565)与前列腺癌数据(GSE5345)当中,数据可以从GEO数据库(https://www.ncbi.nlm.nih.gov/geo)中获得。
GSE2565数据是将小鼠暴露在氯化碳(光气)与空气当中得来的,这会导致小鼠在24个小时内发生不可逆转急性肺损伤和肺水肿,在暴露后的0.5、1、4、8、12、24、48、72小时后分别搜集对照组与实验组小鼠的RNA,而对照组、实验组在每一个时刻分别取6个小鼠样本,以判断肺癌发病的时间。
根据肺癌数据,利用本文构建的个体特异性异常指标的方法,可以得到在时间点t = 8 h时个体特异性异常指标明显增长并达到峰值(图3(A)、图3(B))。其DNB (由临界点变化基因表达最显著的前200个基因组成,下同)中55.4%基因对的
经过z检验其p值小于0.05,于此相对比的在同一时刻对照组的基因对p值小于0.05的占25.21%。
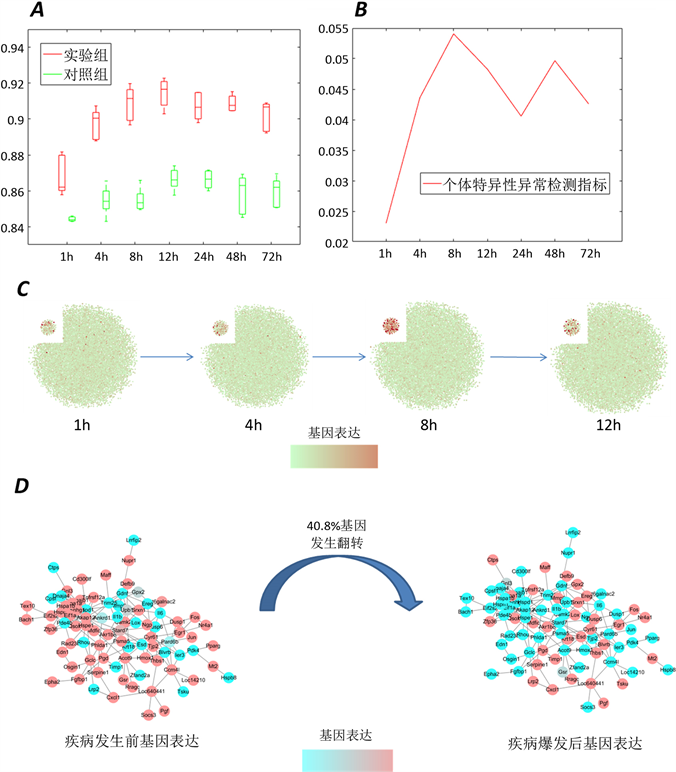
Figure 3. Individual specific abnormal indicator method for lung injury data
图3. 个体特异性异常指标在急性肺损伤数据中应用
利用Cytoscape画出其基因表达与网络动态变化图(图3(C)),其中DNB基因放于左上角的圆形当中。在t = 8时DNB基因表达明显,而在其他时间表达并无明显变化。另外,个体特异性异常指标突增前后基因表达由低表达(高表达)变为高表达(低表达)的基因有40.8% (图3(D)),与其相对比,所有基因平均翻转为10.2%。
上面都指明在临界点前后,基因发生了显著的变化。这与实验结论相一致 [13] :暴露在光气后8小时,BALF蛋白水平升高、肺水肿增加,这导致了存活率降低,在12小时观察到50%~60%的死亡率、24小时后观察到60%~70%的死亡率。这恰好说明暴露于光气8小时进入了疾病爆发期。
研究指出 [14] ,雄激素对前列腺癌细胞系LNCaP有显著的调控作用,GSE5345数据就是通过将前列腺癌细胞系LNCaP暴露在雄激素(以在乙醇作为对照)的实验中,分别在0、6、9、12、18、24和48小时采集RNA得来,每个时间点对照组、实验组分别各有4个数据。
前列腺癌数据中,通过数值实验可以看到,个体特异性异常指标在t = 24 h时候明显增长并达到峰值(图4(A)、图4(B)),其DNB中
经过z检验后p值小于0.05的有48.18%,于此相对比的在同一时刻对照组的基因对p值小于0.05的占33.36%。
针对数据中的DNB数据利用SurvExpress进行生存分析(图4(C)),当DNB基因异常时,前列腺癌病人存活率显著下降,存活时间显著缩短。而针对其DNB中所有基因进行单个生存分析,其对患者存活率有显著影响的基因分别有POLD1,B2M,MBOAT2,DNMT3A,EGR1,SYNPO2,SORBS1,ETV6,ALDH1A2,CD47,EGFR,BCL2L2,STX12,ZNF273,EIFAY,TSTA3,共16个基因。其基因表达与网络动态变化图如图4(D)所示,DNB基因放于左上角,可以看到在t = 24 h基因表达明显,而在其他时间所有基因并无明显表达。DNB基因发生反转的比率占42.3%,而所有基因反转的比率占13.6%。
过去对该数据集的研究中 [15] 指出:在24 h时,雄激素调节的内含子RNA分为三种类型,第一组RNA在24小时内水平下降2~3倍;第二组RNA在24小时内增加2~3倍;第三组RNA在24内增加3~6倍。而三组RNA均在24小时后逐渐恢复。这说明了在24小时为前列腺癌重要临界点。
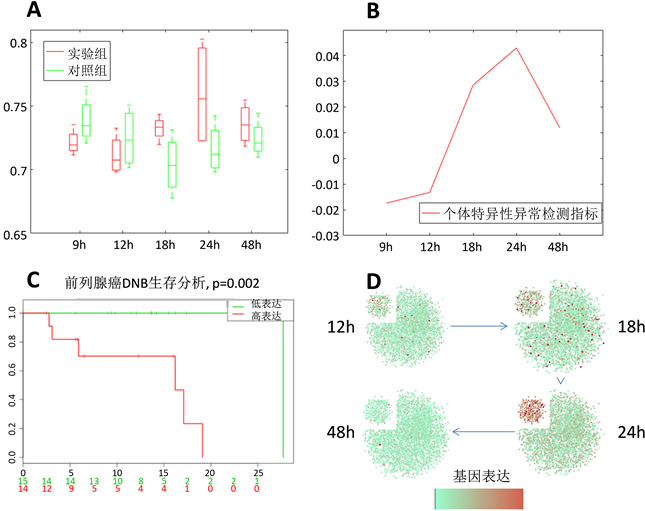
Figure 4. Individual specific abnormal indicator method for prostate data
图4. 个体特异性异常指标在前列腺癌数据中应用
3.3. 功能分析
利用KEGG (https://www.kegg.jp/) [15] 对影响个体特异性异常指标最显著的200个基因进行功能分析(如表2,仅列出部分),其对异常指标影响最显著的200个基因中,所属于通路均与疾病发展联系密切。
针对鼠类肺部损伤数据,KEGG分析结果为主要影响了代谢途径通路、癌症通路、MAPK信号通路等,MAPK与PI3K-AKT信号通路影响细胞的繁衍与凋亡过程,均为受其氧化反应影响的通路。针对前列腺癌数据,最显著的基因中与影响了癌症及相关通路有关(如癌症通路、癌症中蛋白聚糖),同时也与影响MAPK通路等关于细胞增殖与凋亡的通路有关。
4. 讨论
本文通过结合隐马尔科夫模型与构建个体特异性网络的方法构建了一种新的探测临界点的指标,通过提取个体特异性网络中的信息,能够更有效利用实验样本与正常样本具有差异性的信息,聚焦实验样本的特殊性。此外,通过结合机器学习的方法,学习实验样本在正常状态下的表现,更能够分辨下一时刻是否发生变异。也正如此,本文所提供方法不需要提前知道原生物基因网络结构,适用范围更广。
该方法在9个节点理论数据集、急性肺部损伤数据、前列腺癌数据中均通过了验证(图2、图3、图4),在疾病恶化前都发现了异常信号,说明该方法对于探测复杂疾病临界点是有效的。在找到疾病临界点后,一方面对早期治疗有一定帮助,另一方面通过对影响指标的基因的分析,可以找到对疾病影响显著的基因、通路等。对于肺部损伤、前列腺癌中,表2所示通路对其疾病影响显著,结合生存分析,找到POLD1,B2M,MBOAT2,DNMT3A,EGR1,SYNPO2,SORBS1,ETV6,ALDH1A2,CD47,EGFR,BCL2L2,STX12,ZNF273,EIFAY,TSTA3共16个基因对前列腺癌有显著影响。
这项工作有一定的局限性。首先,本文所使用方法与分析具体的病理机制仍然依赖于实验后数据的搜集与临床研究的支持。其次,该方法精度依赖于实验采集的时间点密度、每个时间的样本数量,对时间的精确程度仍然依赖于实验设置时间点,实验时间点之间开始发生异变的时间无法估计(如小鼠肺部损伤实验中,实验得到t = 4 h未进入临界点、t = 8 h已经进入临界点,但再具体的精度仍需要实验支撑),另外由于指标是一个统计性指标,其精度随着实验样本的数量增大而提高,在实验样本量过小的时候这可能是不准确的。
参考文献