1. 引言
随着我国工业生产的繁荣发展,消防、化工、冶金等行业的高温作业问题也日趋严峻,长期在高温和强烈的辐射环境下工作有许多潜在的安全隐患,如热中暑、烧伤和灼伤等危害直接影响着人体的健康安全。高温工作防护服装作为人体与高温环境之间的一层屏障,具有一定程度的隔热和避免灼烧伤功能,是高温作业环境中一项重要的防护措施。它的防护原理是降低热转移速度,让外界高温度的热量缓慢而少量的转移至皮肤。在现今的热防护服的研究领域中,亟待解决的问题是:增强热防护性能与减少人体新陈代谢热负荷总是相互矛盾的 [1] 。基于高温工作防护服装的重要性以及其研究现状,本文通过建立分层热传导方程以及求解其温度–空间–时间分布来分析高温环境下热防护服的不同材质层中的温度变化规律,以辅助于高温工作防护服装的设计问题。模型测试结果显示,与外界相接触的材质层的降温幅度最小,与皮肤相接触的空气层的降温幅度最大。
2. 分层热传导模型
为简化热传递的过程,本文考虑热传递方向是一维的,即只在单位面积皮肤的内法线方向进行热量传递,且在防护服的四层结构中都只存在热传导,而不考虑热辐射和热对流的效应。假定在防护服四层材料之间的连接是无缝隙的,即上一层的下边界与下一层的上边界温度分布相同(从上至下方向为从I层至IV层的方向)。
本文建立的“高温作业防护服–空气–皮肤”的导热模型 [1] 的示意图如图1所示:
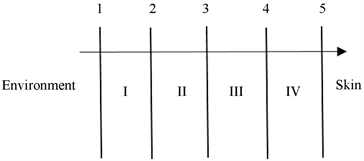
Figure 1. Schematic diagram of thermal conduction model
图1. 热传导模型示意图
如图上箭头所示,其方向为热量传递方向。设
为层内导热方向上每一个位置点与靠近热源的边界之间的距离。在初始状态即
时,认为防护服四层每一个位置节点的温度,都经过假人恒定的体温传导为37℃,外界环境温度固定为一恒定值
℃。设温度为
,时间为
;引入热扩散率
。建立每层热传导二阶偏微分方程如下:
 (1)
(1)
其中
,
表示第
层中的初始空间位置和时间,
,
表示第
层中的终点空间位置和时间。
3. 模型的求解方法
在偏微分方程组的求解过程中,每一个偏微分方程的边界条件是一个很重要的已知条件。若已知不同材质层的边界温度,则该模型可以直接通过偏微分的数值解法直接求得其温度-空间-时间分布。在一般环境中,由于无法通过测量得知每一层的边界温度值,仅可测量出外界环境温度和人体皮肤表层温度,因此,本文分别通过引入热阻的概念来确定不同材质层的边界温度以运用Crank-Nicolson隐式格式求解偏微分方程以及将服装整体化运用古典显式差分法迭代进行求解偏微分方程数值解的方法,来分析高温环境下热防护服的不同材质层中的温度变化规律。
3.1. 基于热阻法求解边界条件以及Crank-Nicolson隐式格式求解偏微分方程
本文考虑类似于电阻在所连支路中限流的作用,引入热阻的概念,将防护服的每一层材料视作具有不同的热量阻碍能力的热阻 [2] 。导热热阻的计算公式为
,其中,
为某层的厚度,
为垂直于热传递方向的横截面积,
为材料的热导率。由相关文献得到:热阻与温度差成正比:
,由不同层之间的热阻比例之间的关系得到热传递过程中每一层的温度差,有:
。
假定外界环境温度固定为一恒定值,经过一段时间后,假人皮肤外侧温度达到热平衡,可求得I层与IV层的温度差,通过热阻计算方法中的比例关系即可求解出不同材质层中的温度改变量,由此可得到每一层的边界条件 [3] 。
利用Sigmoid函数
对不同材质边界处的数据进行函数拟合 [4] ,将所得到的函数作为边界条件,再运用Crank-Nicolson隐式格式差分法 [5] 来求解分层热传导偏微分方程的数值解。
在利用上述差分法求出微分方程解的近似值之前,先对网格的建立进行说明。如图2所示,横向
轴和纵向时间
轴的步长分别为
和
,定义网格比
;绿色边和两条橙色边分别为一个初始条件和两个边界条件。记蓝色边框内的待求解节点矩阵为
(2)
其中 表示 时刻,与靠热源较近的边界距离为
的网格节点的值。
表示 时刻,与靠热源较近的边界距离为
的网格节点的值。

Figure 2. Implicit schematic diagram of Crank-Nicolson
图2. Crank-Nicolson隐式格式示意图
由Crank-Nicolson隐式格式得到的差分形式 [5] 如下:
(3)
由上述格式和边界条件,构造反映时间层
与时间层
之间的关系方程组如下:
(4)
因此,利用第0时间层(初始条件)解出第1时间层的值,由第1时间层解出第2时间层直至第
时间层,这种求解方法称为追赶法。由此可得温度-时间-空间的分布结果,利用2018年全国大学生数学建模竞赛A题 [6] 中的相关数据带入该方法中求解得到不同材质层的温度分布图如图3所示。
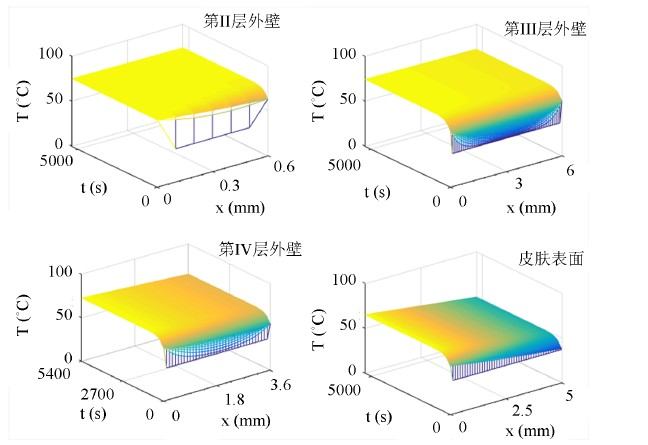
Figure 3. Temperature-time-space Distribution of Layer I-IV Based on the Implicit Method of Solving Partial Differential Equation of CN
图3. 基于CN隐式格式偏微分方程求解法的第I-第IV层温度-时间-空间的分布
从图3、图4可以看出,沿着热传递方向温度不断下降,表明四个不同的材质层对热量的传递都有一定的阻碍作用,且经过一段时间后各自都达到热平衡,即温度不再随时间变化。此外,可看出IV层外壁的温度下降幅度较大,与用热阻判断温度差幅度的结论相符合。

Figure 4. The change of temperature at the last moment (5400 s) with the position based on the method of solving partial differential equation with CN implicit scheme
图4. 基于CN隐式格式偏微分方程求解法的最后时刻(第5400 s)温度随位置的变化
3.2. 基于整体化法以及古典显式差分法求解偏微分方程
首先考虑将四种不同材质层视为一个整体,在已测量出外界环境温度以及人体皮肤表层温度随时间变化的数据的条件下,分别对四种不同材质层中热传导方程运用古典显式差分法 [7] 迭代进行求解偏微分方程数值解。
因古典显格式稳定收敛的充分必要条件是网格比
,若不满足此条件,则可采取扩大步长、扩充矩阵的方法来提高模型求解的稳定性。运用古典显格式进行差分,在节点
上,用向前差商法得到:
整理可得:
(5)
由上式可以看出,第
时间层的节点可以由第 时间层的节点直接推出来,且第0时间层的值是所已知的初始条件,故可以利用这个格式层层递推求解。考虑将防护服内的温度分布作为一个整体,假设四层材料直接连接是无缝隙的,即相邻两层的内外侧温度分布相同,根据这个条件采用迭代的方法,将第
层迭代的结果作为第
层的初始条件,求解得到每一层的温度分布,由 [6] 提供的数据求解得到其整体温度分布结果图如图5。
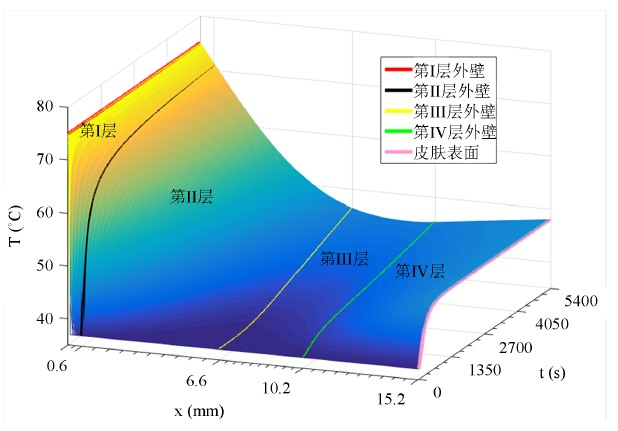
Figure 5. Temperature-time-space distribution of layer I-IV based on classical explicit partial differential equation
图5. 基于古典显式偏微分方程求解法的第I-第IV层温度随时间和空间位置的分布
由图5可以看出,在III层位置呈现“下凹”形态,是由于服装材料在恒温环境下不断吸收热量,服装温度随之升高,从每个升温的瞬间来看,服装相对于身体来说相当于一个热源,因此服装的热量在材质中间某一段会比皮肤表层的温度略小。
为了进一步研究边界处温度变化规律,其I-IV层边界温度随时间变化的数据进行曲线拟合,其结果图如图6所示。
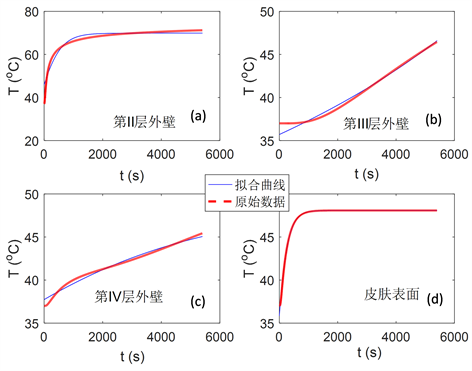
Figure 6. On the basis of the classical explicit partial differential equation solution method, the temperature change of the boundary layer I-IV with time
图6. 基于古典显式偏微分方程求解法的第I-第IV层边界温度随时间的变化
从图6可以看出,四层边界处所求解得结果的拟合效果均较好。其中第II层外壁以及皮肤表面温度经过一段时间后达到稳态,第III层外壁以及第IV层外壁表面温度随时间推移而呈几近线性增长。
4. 模型检验
本文对基于CN隐式格式偏微分方程求解模型进行检验 [8] [9] ,由 [6] 提供的数据,将皮肤外侧温度的测量值进行曲线拟合,比较同一时刻下的计算值与拟合曲线上温度取值之间的差值,误差图如图7。

Figure 7. The calculation and measurement of skin temperature and its error based on the method of solving implicit partial differential equation of CN
图7. 基于CN隐式格式偏微分方程求解法的皮肤温度计算值与测量值及其误差
从误差曲线来看,在实验时间的前段,皮肤外侧的计算值与实际测量值的误差较大,但也都控制在0.04℃以内,说明模型的拟合效果较好。当时间达到大约四百秒之后,误差减小,且在达到热平衡的时间点后,两曲线几乎完全吻合。另一方面,本文假设热传递方向为一维且人体表皮温度为一恒定值,若将该模型扩展至多维方向上且考虑人体表皮温度有变化,只需将人体不同部位的温度数据代入模型中即可 [10] 。若在模型中考虑热辐射和热对流的效应,其结果将会更加精准。
5. 结语
本文建立分层热传导模型来分析热防护服的热量变化规律。利用热阻的概念和整体化两种方法分别拟定偏微分方程组的边界条件,运用Crank-Nicolson隐式格式以及古典显式差分格式分别对该模型进行求解。由于古典显格式稳定收敛的充分必要条件是网格比
,若不满足此条件,需采取扩大步长、扩充矩阵的方法来提高模型求解的稳定性。因此,Crank-Nicolson隐式格式求解法更加简便,且在模型检验中发现,隐式格式求解的数据在达到热平衡后几乎与实际测量值吻合。
基金项目
本文由湖南农业大学大学生创新性实验计划项目(XCX18007)资助。
NOTES
*通讯作者。