1. 引言
当复杂系统的阈值被越过时,会有突然的、长期的变化发生,称为临界转变。近来,对于复杂疾病系统的临界信号的研究也越来越多,如果能够很好的检测复杂疾病的临界信号,对于疾病的掌控是非常有用的。一个疾病系统的随时间或参数动力学过程 [1] 可以分为三个阶段:即前过渡状态、预过渡状态、后过渡状态。1) 在前过渡状态的系统是稳定的,此期间系统缓慢的变化;2) 在预过渡状态的系统是不稳定的,它是前过渡状态的临界情况,给它一个小的扰动或者刺激,系统会进入下一个稳定状态。当系统经过合理的刺激,也可以从这个状态回到上一个稳定状态即前过渡状态;3) 后过渡状态的系统处于另外一种稳定的状态,代表着已经越过了前过渡状态和预过渡状态,对于复杂疾病系统来说,此时疾病处于严重恶化的阶段,尽管病人经过合理的治疗,但是也很难回到正常状态。在生物疾病数据挖掘过程中,很容易受到噪声的干扰,也有非常多的研究表明,噪声对动力系统的影响导致我们的预测是非常不准确的 [2] 。同时在实际疾病的诊断过程中,很难获得大量的实验样本数据,导致我们的样本数据很少,甚至只有一个。对于多样本数据的情况,刘 [1] 等人提出了多样本动态网络生物标志物,可以很好的检测疾病突变的信号。对于噪声干扰的处理,陈 [3] 、刘 [4] 、周 [5] 等人提出了通过矩变换将样本状态转变为样本概率分布,会有一定程度的降低系统噪声。随着生物技术的发展,对细胞基因探测更精准,刘 [6] 等人提出了只有一个实验样本数据时,建立个体差异网络模型,很好的解决了样本数据少的问题,并提供了一个很好的思路。
传统多样本降噪的方法 [4] 为我们提供了多样本概率分布嵌入的方法,将大噪声的样本数据通过矩展开转化为小噪声分布样本数据,然后通过构建动态网络标志物,来预测系统的临界信号。尽管多样本降噪方法可以很好地处理系统所受到的噪声干扰,该方法前提是样本足够多。但对于样本少,甚至只有一个样本时,此时传统多样本降噪方法不适用。本文中对于实验样本数据少并且复杂系统受到噪声强干扰时,结合了概率分布嵌入法和个体特定网络,针对于大噪声的干扰,我们通过一个理论框架即概率分布嵌入模型,将带有大噪声的观测数据通过矩展开的方式转变为高维空间的小噪声分布数据,这里的样本矩对应着一个概率分布,样本状态过渡转变为概率分布过渡,通过预测分布过渡,从而检测出临界信号,达到了降噪的效果。当样本数据较少时,甚至只有一个样本,可以通过个体特定网络方法。利用正常样本建立参考网络,将检测样本加入而构成新的扰动网络,扰动网络和参考网络的差异为个体特定网络,可以准确找到临界点和生物标志物。为了解释方法的可靠性和准确性,将方法应用于肝癌数据(GSE5345)和前列腺癌数据(GSE80018),均成功的探测了临界点信号。并利用STRING得到的蛋白质交互网络,通过Cytoscape作出疾病基因动态变化圆盘图和翻转图,发现动态网络生物标志物中的基因表达临界前后发生了明显的翻转。另外通过对标志物中的基因进行生存功能分析,发现与疾病存活率有很强的关联,说明方法是可靠的。
2. 方法
2.1. 概率分布嵌入法
动力系统理论的研究表明,临界慢化法(CSD) [7] 可作为预测临界转变的方法,临界慢化法的假设是数据在接近临界时只有小噪声的扰动(图1(A-a)),此时方法是有效的。而当系统受到较大噪声扰动的时候(图1(A-b)),此时状态突变会随机提前出现,会远离确定性的分岔位置。即大噪声扰动带来强烈的非线性违反了临界慢化法的假设条件。此时我们采取概率分布嵌入法,通过矩变换将样本状态转变为样本概率分布。根据陈 [3] 的文章,细胞中的基因调控网络受到强噪声干扰时可以由一组Langevin方程表示,其动力系统形如:
(1)
其中
是非线性函数,状态变量
,噪声
,其中
是强高斯白噪声,即
,
。在这里
表示计算平均值的运算符。
在本文中,将系统(1)通过对变量矩展开 [4] 的方式,展开到2阶时,可以表示为以下带有弱噪声的系统:
(2)
其中
表示由非线性函数
通过矩展开产生的,矩变量
,其中矩系统的噪声
,这里
是弱高斯白噪声,即
,
,并且有
,其中 是状态变量的矩,N表示展开到2阶矩的矩变量数,此时有
,其中
表示样本均值(样本的一阶原点矩
),
是协方差(
和
二阶中心矩
。
是状态变量的矩,N表示展开到2阶矩的矩变量数,此时有
,其中
表示样本均值(样本的一阶原点矩
),
是协方差(
和
二阶中心矩
。
将确定动力系统的样本状态方程,如何转化为样本的一阶矩和二阶矩的矩系统方程。首先考虑一个m个分子带有n个反应的生物化学主方程系统,令
表示分子在时间t的状态,定义
表示分子X的概率分布函数,此时通常概率分布动力系统方程可以由主方程 [8] 描述为:
(3)
其中
,
表示分子状态改变值,是一列正向量,即
表示第j个分子在第k个反应方程上的改变量,
表示在第k个反应方程的分子状态从X到
的转化率。通过对
进行泰勒展开到2阶可以得到以下Fokker-Plank方程 [9] :
(4)
根据方程(3)和(4)我们得到其概率状态方程对应的Langevin方程:
(5)
其中
,
是高斯白噪声,并且均值
,协方差
。
因此对于更一般Langevin方程,令
,根据陈的文章 [3] 我们得到以下矩发展方程:
(6)
进一步,当通过对系统(1)矩展开到二阶时,令一阶原点矩
,其中
,二阶中心距(协方差)
其中
,通过(6)我们可以得到:
(7)
(8)
其中,
 (9)
(9)
(10)
对于一个非线性系统来说,当矩样本展开到无穷阶即
时 [4] ,此时系统受到噪声的大小是接近于0的,换句话说当样本矩的阶数越高,所得到的动力学分布就越准确即噪声越小,这一结果为我们通过矩展开的方式来降低噪声水平提供了理论基础,此时矩系统对应着动力学分布系统。对于矩展开到无穷阶往往比较困难,并且许多有关截断矩的复杂方案研究 [5] ,以及对矩封闭性 [10] 的要求,所以我们会对系统样本矩展开到有限维,此时噪声非常小。
2.2. 个体特定网络
根据刘 [6] 的文章等人提出的个体差异网络的思路,个体特定网络是基于该个体相对于一组给定对照样本的统计扰动分析而构建的。因此我们需要一组样本表达数据作为正常样本,利用正常样本(n个正常样本)分子间的相关系数构建参考网络(图1(B)),将n个样本分子间的皮尔逊相关系数作为网络的边记为
,当新加入一个测试样本时通过同样的方法构建扰动网络记为
,将扰动网络与参考网络的差作为个体特定网络记为
。即
。此时
即表示测试样本的个体特定网络,因为测试样本带来的变化,可以通过分析个体特定网络来研究测试样本。如果测试样本是正常样本,我们知道扰动网络和参考网络变化不大,即
很小。相反,当测试样本时疾病样本时,基于分子的显著表达,扰动网络和参考网络会有显著差异,即
很大。
(A)中(a, b)表示单变量动态系统在不同噪声下随着参数或时间的表现行为。(a)表示单变量系统在小噪声下时,临界点和系统分岔点位置非常接近,此时传统方法(如临界慢化方法)可以检测预警信号。(b)表


Figure 1. Model of probability distribution embedding and individual specific network
图1. 概率分布嵌入模型与个体特定网络
示单变量系统在大噪声下时,此时临界点随机的远离系统分岔点,通过CSD方法无法检测预警信号。(c)通过矩展开,带有大噪声的观测数据通过矩展开的方式转变为高维空间的小噪声分布数据,这里的样本矩对应着一个概率分布,样本状态过渡转变为概率分布过渡,通过预测分布的动态行为,可以发现CSD方法是有效的。(d)可以物理的解释为将原系统的大噪声分解到升维的两个矩平面,此时样本X大噪声动力系统,变成了小噪声的矩样本动力系统。(B)中表示当加入测试样本的时候的个体特定网络,即可以通过扰动网络和参考网络的相关系数差计算
。
2.3. 个体特定网络概率嵌入法动态网络标志物综合指标
当生物数据测试样本比较少时,甚至只有一个样本。对于大噪声的数据,此时我们采取个体特定网络概率分布嵌入模型,即结合概率分布嵌入法和个体特定网络。首先通过概率分布嵌入法,将样本状态数据转化为概率分布动态数据。然后引入个体特定网络,将正常样本作为参考网络,当加入测试样本形成新的扰动网络,扰动网络与参考网络之间的差异我们称为个体特定网络。基于前面的理论分析,类似多样本降噪法 [4] ,对于此时动态网络标志物满足以下三个条件:
1) 显著组中的每个变量的表达均值差的绝对值(
)明显增加;
2) 显著组中的变量之间的皮尔逊相关系数差的绝对值(
)明显增加;
3) 显著组中的变量与非显著组中的变量之间的皮尔逊相关系数差绝对值(
)明显增加。
引入个体特定网络标志物综合指标
:
(11)
对于同时满足以上三个条件,此时
值达到最大或者急剧增加,即该时刻达到临界状态,从而得到动态网络生物标志物。
动态网络生物标志物(DNB)提供了一个观察小噪声系统预警信号的理论基础,并且通过DNB预警疾病系统信号是成功证实的 [1] [4] ,在本文中,我们结合概率分布嵌入法和个体特定网络,最后利用DNB来检测预警信号。
3. 基于个体特定网络概率嵌入法算法流程
基于上述理论基础,对于给定数据,当样本数据只有一个样本时,此时我们结合了概率分布嵌入法和个体特定网络,计算个体特定网络概率嵌入法动态网络标志物综合指标
,具体步骤如下:
第一步:标准化
(12)
(13)
表示正常样本的数据,
表示疾病样本的数据,N和D分别表示标准化正常样本和疾病样本的数据,
,
分别表示正常样本的均值和标准差。
第二步:筛选基因
在每个时间点,设置显著性水平p < 0.05或者p < 0.01对数据进行T-检验,以及差异表达挑选出在正常样本和疾病样本间具有显著差异的基因。
第三步:矩升维
计算每个样本每个时间点的一阶矩和二阶矩。
第四步:计算基因表达偏差
(14)
计算每个基因表达偏差值,设置合理的阈值筛选基因,其中g表示疾病样本基因的表达值,
正常样本基因的表达值均值。
第五步:确定DNB和计算
首先利用皮尔逊相关系数差值的绝对值对基因聚类。根据理论可知,当新的测试样本是疾病样本的时候,表达偏差会突然增大,同时皮尔逊相关系数差值也会显著增大,此时找出聚类结果满足
综合指标三个条件即可确定备选的DNB,从而确定DNB。
计算综合指标
,
(15)
其中,
是基因表达偏差,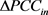 表示DNB组内基因扰动网络与参考网络差绝对值的均值,
表示非DNB基因的扰动网络与参考网络差的绝对值的均值。
表示DNB组内基因扰动网络与参考网络差绝对值的均值,
表示非DNB基因的扰动网络与参考网络差的绝对值的均值。
4. 应用
接下来我们将上面方法应用在肝癌数据(GSE80018)和前列腺癌数据(GSE5345) (https://www.ncbi.nlm.nih.gov/gds/?term=),数据下载自NCBI的GEO数据库,当样本数据少,基于个体特定网络概率嵌入法能够依据少量样本数据检测临界信号确定临界点,根据计算两个数据的个体特定网络标志物综合指标 确定时间点。根据肝癌数据,利用个体特定网络概率嵌入法检测到5个样本均在第3天的时候发生突变(图2(a)),并且此时分别有动态网络标志物235,298,210,271,260个,其中包含转录因子,他们两两之间共同基因分别有162,142,162,154,145,173,157,152,152,166,并且对这237个基因进行生存分析等功能分析,并通过肝癌动态网络标志物以及STRING得到的蛋白质交互网络,利用CytoScape画出疾病基因动态变化过程圆盘图和翻转网络(图2(c),图2(d),结果与实验观测吻合,实验数据是苯巴比妥(PB)介导的体内肝肿瘤促进早期阶段的分子和病理扰动的时间序列,在自由采食PB (饮用水中0.05% [wt/vol])给药的小鼠中进行动力学研究(治疗1,3,7,14,28,57和91天),PB处理影响肝脏中大量基因的转录,在研究的至少一个时间点内显着失调的约2000个基因。因为细胞周期/有丝分裂相关基因的瞬时上调,在PB处理1天后检测到最大数量的转录变化。同时药物代谢基因被强烈上调以及在整个13周的研究中它们的表达仍然很高。并且和转录分析一致,PB诱导的异生素代谢酶(包括CYP450酶和还原酶POR)的蛋白质水平变化明显,检测到的最显着的组织病理学异常是从PB治疗7天开始观察到的肝细胞肥大,并且在稍后的时间点严重程度增加 [11] 。根据前列腺癌数据,利用个体特定网络概率嵌入法检测到4个样本均在第24小时的时候发生突变(图2(b)),并且此时分别有动态网络标志物220,257,253,230个,其中包含转录因子,它们两两之间共同基因分别有112,87,90,90,90,127,并通过对这161基因进行生存分析等功能分析。结果与实验观测吻合,用合成雄激素(R1881)或乙醇载体(对照)处理前列腺癌细胞系LNCaP,并在几个时间点(0、6、9、12、18、24和48小时)采集RNA进行分离。用微阵列(SAM)的显着性分析来鉴定在暴露于雄激素后0~48小时的时间段中显示出统计学上显着的水平变化的转录物。研究显示雄激素调节的内含子RNA可以根据雄激素暴露后不同的表达时间模式分为三组。簇I含有RNA,其在雄激素暴露后24小时内水平下调2~3倍,并在48小时后恢复。簇II和III包括内含子RNA,其在24小时内被雄激素上调并且随后恢复。簇II分组的RNA增加了2~3倍,而簇III分组的RNA被上调了3~6倍 [12] 。
5. 总结
针对于数据受到强噪声的干扰和实验数据样本少的情况,结合了概率分布嵌入法和个体特定网络,首先通过概率分布嵌入,将样本状态数据转化为概率状态数据,此时低维的大噪声数据转化为高维的小噪声数据,再通过利用正常样本建立的参考网络与加入实验样本建立的扰动网络,构造个体特定网络,通过验证综合指标,找出动态网络生物标志物,可以很好的探测疾病的临界信号。
对于一些实际数据,很难用确定性方程表达刻画,个体特定网络概率分布嵌入法同样适用于非确定性复杂系统,此时用于肝癌数据和前列腺癌数据,都成功的探测出了临界信号(图2(a),图2(b))。对于肝癌数据,利用动态网络生物标志物和生存分析找出23个基因(ATG9A, BDH1, CENPW, DPY19L2, GXYLT1, INHBA, MLF1, NEDD4, PA2D4, PAH, PKIA, POU2F1, PTPN12, RGS5, RUSC2, SEH1L, SV2A, TCP1, THAP4, TRPM6, TUBGCP, TXLNA, VAX1)当这些表达异常时,肝癌患者存活率下降,生存时间变短(图3(a))。这些基因中很多被证明和癌症的发展以及病变有关,含有TCP1的伴侣蛋白CCT8会促进肝癌细胞增殖 [13] ,MLF1在神经母细胞瘤肿瘤发生中起重要作用 [14] ,BDH1肝脏脂质分解代谢有关,对肝功能的影响是至关重要的 [15] 。对于前列腺癌数据,利用动态网络生物标志物和生存分析找出15个基因(CCNA2, CSNK1D, CSNK1G2, ECT2, FOXN2, HOXB6, HPGD, LIMK1, MAGI1, PLK1, PTBP1, RAD51AP1, RALB, SEMA4D,

 (a)肝癌数据,∆ISCI指标在第二个时间点即第3天,信号突然增强,有临界信号产生。(b)前列腺癌数据,∆ISCI指标在第六个时间点即第24小时,信号突然增强,有临界信号。(c) (d)分别表示肝癌疾病基因的动态变化圆盘图以及DNB翻转网络。
(a)肝癌数据,∆ISCI指标在第二个时间点即第3天,信号突然增强,有临界信号产生。(b)前列腺癌数据,∆ISCI指标在第六个时间点即第24小时,信号突然增强,有临界信号。(c) (d)分别表示肝癌疾病基因的动态变化圆盘图以及DNB翻转网络。
Figure 2. The applications of individual specific network and moment expansion in two real data and dynamically changes in the network including the DNB and overturn network during the progression of liver cancer
图2. 基于个体特定网络分布嵌入法检测真实数据集的临界信号和肝癌圆盘图以及翻转网络


Figure 3. Survival analysis based on individual specific network and moment expansion of liver cancer and prostate cancer
图3. 基于个体特定网络概率嵌入法生物标志物的肝癌和前列腺癌生存分析
SMARCA4)当这些表达异常时,前列腺癌患者存活率下降,生存时间变短(图3(b))。同样这些基因很多被研究证实与前列腺癌的病变有关,其中CCNA2的下调可以有效抑制癌细胞的增殖和迁移,并诱导细胞凋亡和细胞周期停滞 [16] ,ECT2和癌症细胞分裂以及细胞周期密切相关,PLK1协同调节转录激活因子STAT3或者直接作为复合物与STAT3结合促进癌细胞迁移 [17] ,可以发现这些基因和前列腺癌的病变发展密切相关。