1. 引言
人口问题是一个巨大的社会性问题,一个地区人口的发展会影响到该地区的社会、经济和环境资源等各个方面,因此,对人口的有效预测能为将来制定合理的发展方案提供有力依据。
云南省是人口大省,作为国家东南亚和南亚开放的门户,在一带一路的国家战略带来的机遇下,对云南省人口的有效的预测能为其制定合理的发展方案提供有力依据,因此,建立一个精度高的云南省人口数量模型就显得尤为重要了。
预测人口应该结合人口的发展特点来进行,由于人口数量当前受前期影响较为大,而通过简单分析能得出云南省近45年来人口呈现接近线性方式增长的结论。结合这些特点,本文旨在通过构建一元线性模型和ARIMA模型来对云南省人口数量模型进行拟合,并从中选取精度最高的模型作为云南省人口数量模型,以此来预测云南省的人口数量的发展。
2. 文献综述
人口问题是一个世界性问题,这影响到社会的方方面面,从而对人口的有效预测也就成了一个非常重要的问题。田飞 [1] 对人口预测的方法体系进行的研究,总结出人口预测模型发展的历程:较早期的模型有指数增长模型、Logistic模型和线性回归模型,随着模糊数学和统计学的发展出现了灰色系统GM (1,1)模型和时间序列模型,而生物医学和计算机的发展为此带来了神经网络算法 [2] ,这些算法各有优缺点,在模型的选取上应该结合不同数据的特点选择合适的模型。
人口的预测模型应结合当地人口发展的特点来选取。云南省的人口特点除了包含当期人口规模受前期人口影响较大这个几乎所有人口都有的特点以外,还呈现接近线性方式增长的特点,第一个适用于ARIMA模型,第二个适用于线性趋势模型。这两个模型应该都十分广泛,其中第二个模型就是普通的以时间序号为自变量的一元线性模型,易于理解不做过多介绍。
时间序列模型在分析前期对当期有影响的数据时具有非常广泛的应用。如李子奈等 [3] 使用时间序列模型分析和预测了我国的通货膨胀情况,结果表明时间序列模型的精度高。张松林等 [4] 使用时间序列模型分析我国的城市化水平,并给出高精确度的预测结果;唐毅 [5] 在传统时间序列模型的基础上,从样本序列的动态选取及模型识别两方面进行优化,提出了一种能动态调整模型参数的改进时间序列模型。而在近两年的研究中,时间序列的应用有了更广泛的实际应用,如王莉等 [6] 使用时间序列模型结合残差控制图分析了兰州市的空气质量指数,证实了将时间序列模型与残差控制图结合预测监控大气污染的有效性。刘自强等 [7] 运用关键词群分析、社会网络分析和时间序列模型分析预测其研究热点的发展趋势,结果表明该方法的有效性。这也进一步表明了传统的时间序列模型与新方法的结合能有效克服传统时间序列模型缺陷,有效解决时代发展的新问题。
云南省人口发展当前受前期影响大,且呈现接近线性方式增长。正是基于以上分析,我们分别使用ARIMA模型和线性模型来对云南省人口数量模型进行拟合,并从中选取精度最高的模型作为云南省人口数量模型,以此来预测云南省的人口数量的发展。
3. 理论知识
3.1. 趋势拟合法——线性模型 [8]
趋势拟合法用于拟合具有趋势项的数据,把时间作为自变量,相应的序列观察值作为因变量,建立序列值随时间变化的回归模型的方法。而当数据呈现线性或接近线性方式增长时,使用线性模型来拟合即可。此时模型表达式为:
其中
为随机波动,
为消除随机波动的影响之后该序列的长期趋势。
3.2. ARIMA模型 [9]
具有如下结构的模型称为求和自回归移动平均模型,简记为
模型:
式中,
,为平稳可逆
模型的自回归系数多项式;
,为平稳可逆
模型的移动平滑系数多项式。
3.3. 精确度评价
本文使用
表示实际值,
表示实际值表示预测值,n为样本数。
1) 均方误差(RMSE):
2) 平均绝对百分比误差(MAPE):
显然,均方误差(RMSE)和平均绝对百分比误差(MAPE)越小,说明模型预测精确度越高,误差越小,模型拟合效果也就越好。
4. 模型构建
本文使用R语言 [10] 进行模型的构建。本文选取1973年至2017年共45年的云南人口数量数据(本数据来源于《云南省统计年鉴》,单位为万,用x表示),画出其趋势图见图1。
从图1可得出,云南省人口数量一直呈现递增的趋势,且增长趋势接近线性趋势,从而使用趋势拟合法中的线性模型来进行拟合。
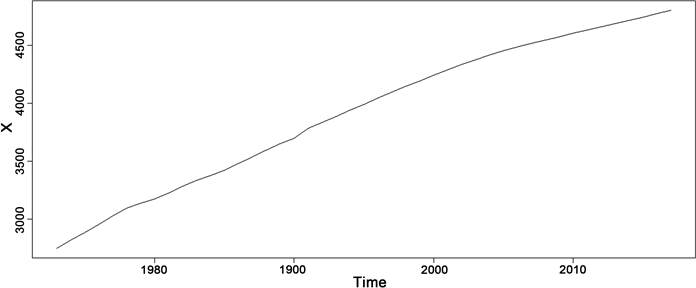
Figure 1. Population trend map of Yunnan Province in the past years
图1. 云南省历年人口趋势图
4.1. 趋势拟合法——线性模型
1) 模型拟合
此模型是时间作为自变量,相应观察值作为因变量的一元线性模型,得出模型拟合结果(t表示作为自变量的时间):
(1)
2) 模型检验
模型(1)的
;常数项的
;系数t的
,此三者均小于显著性水平
,表示模型(1)及其系数t均显著,模型(1)合理。
3) 精度评价
依据模型(1)可以计算通过此模型得出的云南省1973年至2015年人口数量的估计值,RMSE和MAPE,得:
4.2. ARIMA模型 [8]
1) 数据预处理
通过图1中显示的人口数量递增趋势可知x为非平稳序列,我们对其进行逐步差分,并对逐步差分的结果进行DF检验,以判断逐步差分后序列的平稳性。
一阶差分
;二阶差分
,则二阶差分后序列(用x1表示)能通过平稳性检验,本文选用差分两次的序列来拟合ARIMA模型。
2) 模型拟合
我们这里画出x1的自相关和偏自相关图,以判断ARIMA模型中的自回归和移动平均的阶数。该图见图2。
从图2可以看出,1期的ACF值在二倍标准差之外;5期的ACF值在刚好等于二倍标准差;1期的PACF值在二倍标准差之外,从而我们尝试拟合包含一阶自回归、一阶移动平均和一阶自回归、五阶移动平均的ARIMA模型。
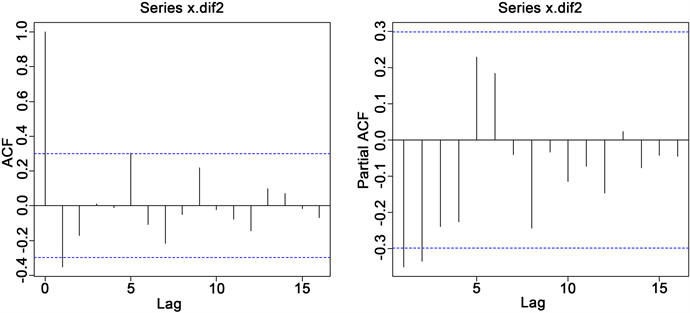
Figure 2. Autocorrelation diagram and partial autocorrelation diagram of x1
图2. x1的自相关和偏自相关图
我们拟合的这两种模型的AIC值分别为315.41和315.82,以AIC值最小准则选取一阶自回归、一阶移动平均的ARIMA模型较为合理。从而拟合的模型为:
(2)
3) 模型检验
我们这里对模型(2)进行纯随机性检验,6期和12期检验结果的P值分别为0.3365和0.1915,此二者均大于显著性水平
,表明模型(2)通过残差的随机性检验,模型(2)是合理的。
4)精度评价
依据模型(2)可以计算通过此模型得出的云南省1973年至2015年人口数量的估计值,并以此计算RMSE和MAPE,得:
4.3. 模型比较
我们以均方误差(RMSE)和平均绝对百分比误差(MAPE)作为评价,模型精确度的指标,此二者值越小说明模型拟合效果越好。模型(1)和模型(2)的精度比较见表1。

Table 1. Precision comparisons of Model (1) and Model (2)
表1. 模型(1)和模型(2)的精度比较表
从表1可以看出,ARIMA模型的RMSE值和MAPE值两个指标都比线性模型的小,这表明ARIMA模型精度都大于线性模型,从而我们选取模型(2)作为云南省人口数量的预测模型。
5. 模型预测
我们得出的云南省人口预测模型为:
(2)
使用R语言对模型(2)对云南省今后5年的人口数据进行预测,得出的预测值及其95%置信区间间表2。

Table 2. Population forecast value table of Yunnan Province in the next five years
表2. 云南省今后5年人口数量预测值表
我们这里计算真实的云南省2013年~2017年人口增长率为22.6,预测的2018年~2022年的人口增长率为22.944,此二者值非常接近。这说明云南省未来五年的人口将会基本保持目前速度。
6. 结论
本文根据云南省人口当期受前期影响大,且增长呈现接近线性趋势的特点分别构建了ARIMA模型和线性模型,以均方误差(RMSE)和平均绝对百分比误差(MAPE)作为评价精度的指标,结果表明ARIMA模型的精度最高,最终选取ARIMA模型作为云南省人口数量模型。
本文以ARIMA模型预测云南省未来五年的人口数量,预测结果表明云南省未来五年人口将保持稳定增长,且预测未来五年(2018~2022年段)人口数量曲线的斜率与2013~2017年段曲线斜率非常接近,这说明增长速度与目前增长速度基本相同。
基金项目
本文得到了云南财经大学研究生创新基金项目(2018YUFEYC001)的资助。