1. 引言
Gronwall型积分不等式和它们的各种推广形式在讨论微分方程解的存在性、唯一性、连续性、有界性、稳定性和不变流形等方面有着十分重要的作用。关于连续函数的积分不等式及其应用方面已有很多结果,如文献 [1] [2] [3] [4] 等。
脉冲是指电子电路中的电平状态突变,既可以是突然升高(脉冲的上升沿),也可以是突然降低(脉冲的下降沿)。一般脉冲在电平突变后,又会在很短的时间内恢复原来的电平状态。在机械工程中常见这种现象,体现在数学上就是脉冲微分方程。实际中,我们经常需要讨论脉冲微分方程解的存在性问题,而这个问题又会涉及到脉冲积分不等式(即,非连续函数的积分不等式)。对含脉冲项的积分不等式的研究主要是为了解决具有脉冲扰动的微分方程、积分方程和泛函微分方程解的定性性质,如解的有界性、吸引性、稳定性等。
最近越来越多的学者开始关注含脉冲项Gronwall型积分不等式。Samoilenko和Perestyuk [5] 于1987年为讨论脉冲微分方程研究了如下的脉冲积分不等式
, (1)
其中
是常数,
是
的第一类不连续点。
2005年,Samoilenko和Perestyuk [6] 用单调不减函数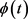 代替常数
代替常数 讨论了如下Bellman-Bihari型积分不等式
讨论了如下Bellman-Bihari型积分不等式
。 (2)
2007年,Iovane [7] 又研究了含时滞项
的非连续函数积分不等式
。 (3)
此后,关于这类积分不等式的新改进和推广不断出现 [8] [9] [10] [11] 。2009年,Gallo和Piccirillo [8] 研究了含时滞项
及非线性项
的非连续函数Bellman-Bihari型积分不等式
。 (4)
受前面方法的启发,本文欲将不等式(4)推广到如下含时滞项及
个非线性项的形式
。 (5)
2. 主要结果
假设
(H1)
是定义在
的非负单增连续函数且
;
(H2) 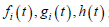 是定义在
上的非负连续函数,
是定义在
是定义在
上的非负连续函数,
是定义在 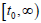 的非负可导函数,且
,
时
的非负可导函数,且
,
时  ;
;
(H3) 是定义在
上的非负分段连续函数,其中
,
是
的第一类不连续点,
且
;
是定义在
上的非负分段连续函数,其中
,
是
的第一类不连续点,
且
;
(H4)
是定义在
上的单调不减连续函数,且当
时,
;
(H5)
都是常数且
。
定理:假设条件(H1)~(H5)成立,且
满足不等式(5)。如果对任意
,
,令 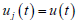 ,则函数
的估计可由下式递归给出
,则函数
的估计可由下式递归给出
(6)
其中
(7)
(8)
并且
,
, (9)
且
。
证明:首先,考虑
即
,此时(5)中不含有脉冲项,故(5)式变为
。 (10)
先讨论
情形。
令
, (11)
则 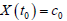 ,
,即
,且
为
上非负不减函数。(11)式两边对
求导,有
,
,即
,且
为
上非负不减函数。(11)式两边对
求导,有
。
而
,所以
, (12)
即
。 (13)
(13)式两边对
从 到
积分得
到
积分得
。 (14)
记
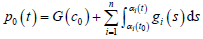 , (15)
, (15)
则
 。(16)
。(16)
任取
,因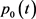 为非减函数,故对于任意
有如下不等式成立
为非减函数,故对于任意
有如下不等式成立
。 (17)
(17)式右端为
,则
为非减函数,
且
,
对
求导得
。 (18)
从而
。 (19)
(19)两边对
从 到
积分,得
到
积分,得
,
即,
。 (20)
所以,
(21)
由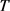 的任意性,用
代替
,即有
的任意性,用
代替
,即有
(22)
若
,选取小正数 ε > 0 代替
,然后让
趋于0,同样证明。
所以对于
,
,用
代替(22)中的
,估计式(6)成立。
时,
,此时不等式(5)有脉冲项。将(5)变形为
, (23)
这里
的定义如(7),
的估计式见(22)。如果用
和
代替
和
, 代替
(
如(8)式定义),(23)式完全类似于(10)式。故
代替
(
如(8)式定义),(23)式完全类似于(10)式。故
 (24)
(24)
故对于
,
,用 代替(24)中的
,估计式(6)成立。
代替(24)中的
,估计式(6)成立。
假设对任意
估计式(6)成立,即
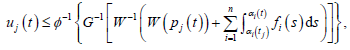 (25)
(25)
则当
时,由(5)知
(26)
这里
的定义如(7)。由假设知
时,
的估计式可由(25)给出,同样用
和
代替
和
,
代替
,(26)完全类似于(10),故有
 。 (27)
。 (27)
综上所述,估计式(6)成立,定理得证。
基金项目
2018年岭南师范学院校级科研项目(理科)重点项目(LZ1806)。
NOTES
*通讯作者。