1. 引言
随着现代科学技术的迅猛发展,网络化系统变得越来越重要。通常研究的网络化系统往往都是线性系统,而在现实生活中,系统往往都具有非线性,而且这种非线性往往都是随机发生的,因此研究非线性化网络系统显得越来越重要。
状态估计问题是控制工程领域与航空航天领域的研究重点。它是基于已知的测量输出,运用经典卡尔曼滤波理论估计出系统内部未知的信号,或者是还原受噪声扰动的真实的信号。目前而言,状态估计涉及的领域十分广泛,包括航天、军事、控制工程等领域都或多或少会用到状态估计的相关理论,具体而言,在目标渐进跟踪、多波次导弹齐射、卫星定位等方面都有具体应用。另一方面,系统中的非线性部分往往是随机发生的,往往会呈现出多样性等特点,但是相对于线性系统的状态估计,非线性系统的状态估计研究的相对较少。故而,非线性系统的状态估计问题引起了国内外专家学者的广泛关注。
随着科学技术的不断进步与发展,状态估计理论要解决的问题也越来越广泛与复杂。由于在估计器的设计及参数实现过程中,不可避免地存在着不确定因素,使得估计器参数不可能准确实现,从而导致系统的性能变差甚至不稳定。于是,要求所设计的估计器具有一定的调节能力来满足系统性能的需要,也就是所设计的估计器要有一定的弹性。在过去的几十年里,关于状态估计器的弹性问题得到了广泛的关注 [1] - [13] 。文献 [14] 解决了具有耦合时滞的Markov跳变复杂网络的状态估计问题,考虑了估计参数不确定性是与网络节点和模态相关的情形,提出了更具鲁棒性的状态估计方法。文献 [15] 考虑了多重测量丢失和概率发散扰动对时变动态网络的影响,解决了该类网络的弹性H∞状态估计问题并给出了相应的状态估计设计方法。因此,研究这类现象显得尤为重要。
2. 主要结论
在本文中,考虑如下的时变系统:
(1)
式中,
为k时刻系统的状态变量,
是测量输出;
、
均为非线性函数;
是均值为零方差为
的过程噪声;
是均值为零方差为
的测量噪声;
均为系统矩阵;
与
均为服从伯努利分布的随机变量,分别刻画随机发生的非线性与随机发生的不确定性,并满足以下条件:
(2)
其中
与
是已知的常数。
假设:非线性函数
满足如下的利普希茨条件:
(3)
非线性函数
满足如下的利普希茨条件:
其中l为已知的利普希茨系数。
在本文中,构造如下形式的滤波器:
(4)
式中
是
在k时刻的状态估计,
是
在k时刻的一步预测,
是
时刻的状态估计,
是
时刻的滤波增益矩阵,
为增益扰动矩阵,
均为刻画增益扰动的矩阵,
是已知的适当维数的矩阵,矩阵
未知满足
,I为单位矩阵。
本文主要有以下两个目的。第一,针对具有随机发生非线性的时变系统设计形如(4)的滤波器,得到滤波误差协方差矩阵的上界,即找到一正定矩阵
满足如下关系式:
(5)
第二,通过设计适当的滤波器增益使得滤波误差协方差矩阵上界的迹达到最小。
3. 具有随机发生非线性的递推滤波器设计
首先,介绍如下几个引理:
引理1 对于两个实列向量
,则下面的不等式成立:
(6)
其中
是已知的正数。
引理2针对适当维数的矩阵
,F满足
,令X是一个正定对称矩阵,且
是一个正数,满足
,
则如下不等式成立
(7)
为了书写方便引入如下记号:
,为一步预测误差,
,为滤波误差,
从(1)~(4)可得
(8)
同理得到滤波误差
(9)
引理3 系统状态的协方差矩阵的上界
表达式如下
(10)
证明:
其中
(11)
应用引理1可得
其中
为正常数,则有
(12)
根据不等式性质得到
(13)
将上式代入(12),得到系统上界协方差矩阵的表达式
(14)
定理1 一步预测误差协方差
的递推表达式如下:
(15)
其中
为滤波误差协方差。
证明:
根据一步预测误差表达式(8),很容易得到定理1,故而证明从略。
定理2 滤波误差协方差
的递推表达式如下:
(16)
其中
证明:
根据滤波误差表达式(9),很容易得到定理2,故而证明从略。
定理3 考虑定理1和定理2给出的一步预测误差协方差和滤波误差协方差。令
,
,
,
是大于零的数,如果下述黎卡提型差分方程
(17)
在初始条件下
有正解
和
,并满足以下两个约束条件:
则矩阵
是
的上界。进一步而言,若滤波器增益采取如下形式:
(18)
那么可以保证上界
的迹达到最小。
证明:
考虑到定理1中的交叉项L,应用引理1可得
(19)
其中
是一个大于零的标量。将上述不等式代入(15)可得
(20)
由于
(21)
故而
(22)
将公式(22)代入(20),可得
同理可得
(23)
其中
是一个标量。将上式带入到(16)有
(24)
接下来应用引理2,
(25)
(26)
将上面两个不等式代入(24)
(27)
最后,证明由公式(18)给出的滤波器增益是最优的。对(17)的迹关于滤波器增益
求偏导,并且令偏导数等于零,得到滤波器增益
如下所示
(28)
证毕。
4. 数值仿真
在本部分中,给出数值仿真来说明所提出的算法的有效性。
考虑如下的系统参数:
,
,
,
,
,
,
,
,
,
,
;
在本仿真实验中,系统的初始值
,
估计状态的初始值为
,
估计误差协方差矩阵的初始值
。具体仿真效果图如图1至图4所示。
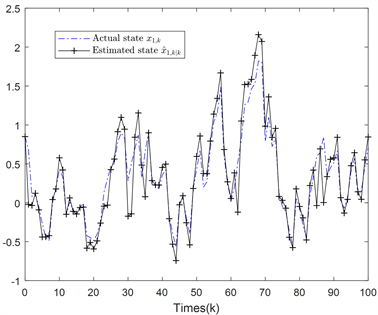
Figure 1. Contrast diagram of actual state trajectory
and its filtering trajectory
图1. 实际状态轨迹
及其滤波轨迹
对比图
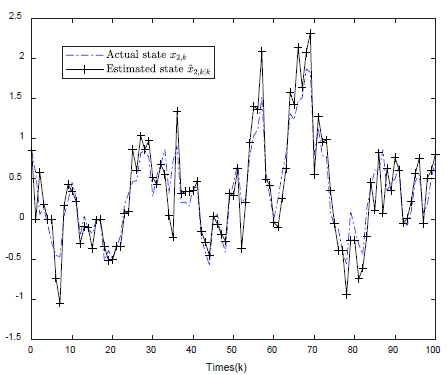
Figure 2. Contrast diagram of actual state trajectory
and its filtering trajectory
图2. 实际状态轨迹
及其滤波轨迹
对比图
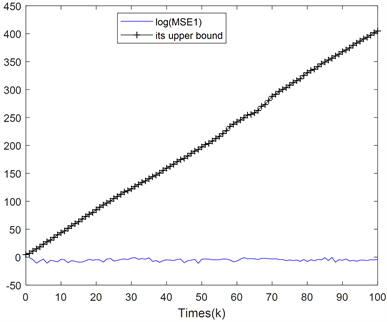
Figure 3. Mean square error logarithm
of filter
and its minimum upper bound contrast graph
图3. 滤波
的均方误差对数值
及其最小上界对比图
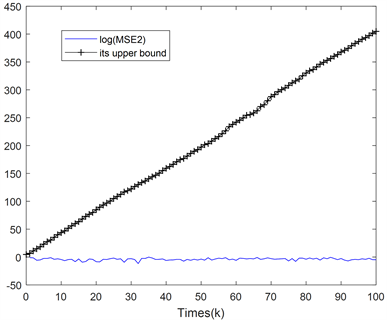
Figure 4. Mean square error logarithm
of filter
and its minimum upper bound contrast graph
图4. 滤波
的均方误差对数值
及其最小上界对比图
5. 结论
在本文中,研究了具有随机发生非线性的滤波问题,为了体现非线性的随机性,引入了服从伯努利分布的随机变量刻画随机发生的非线性。与此同时,为了保证所设计的滤波器对增益扰动具有鲁棒性,在设计滤波器时引入了弹性。通过解黎卡提型差分方程,得到滤波误差协方差矩阵的上界,通过设计滤波增益矩阵使得该上界的迹达到最小。