1. 引言
经济问题是当今世界的热点问题,世界各国学者和专家围绕各种经济问题,做了大量的工作,其中,对于宏观经济系统的学习与研究,是一个非常重要的课题。宏观经济系统本身是一个极其复杂的大系统,影响因素多样,很难用一个数学模型对其进行准确描述。当建立起一个经济大系统模型时,可能因为参数估计不准确或时间变化而导致结构不稳定——分支现象,Hopf分支就是其中一种。
本文为经济大系统的研究提供了一个相对简化的新思路和新的模型参考,同时研究了新模型的稳定性和结构不稳定现象,将Hopf分支现象进一步与实际模型相结合,为国家宏观经济政策的制定提供了一个参考,也是将数学结论应用于实践的一种尝试。
线性宏观经济系统模型如凯恩斯模型、萨缪尔森乘数-加速数模型、希克斯模型已无法符合当今经济的发展趋势,随着经济学的发展,现如今,大量的经济系统模型已被提出,“控制论”的思想被引入经济界。将整个经济社会的动态发展看做动态大系统,此时,经济问题相对合理地转变为数学问题,可用数学方法与数学工具对其进行研究。刘永清、宋中昆在分解理论在经济大系统中的应用 [1] 的就讨论了此类问题。Hopf分支理论已成为研究微分方程小振幅周期解产生和消亡的经典工具,马知恩、周义仓所著的《常微分方程定性与稳定性方法》 [2] 对Hopf理论做了详尽阐释和介绍。
2. 预备知识
今考虑系统
(1)
或记以下形式
(2)
式(2)不含时滞的线性时变系统为
(3)
式(2)、(3)的孤立子系统为
(4)
其中
。设(1)的系数连续、有界、可微。
(5)
(6)
(7)
(8)
引理1:若(1)的系数连续有界可微,条件(5)、(6)、(8)成立,有
,即线性时变子系统(4)的零解是渐近稳定的,存在
,则具有时滞的时变系数线性系统(2)的零解也是渐近稳定的。
设当
(9)
当
,类似得到
(10)
从而得到当
,即
时,孤立子系统(4)的零解是不稳定的。
引理2:若系统(1)的系数连续有界可微,条件(5)、(9)、(10)成立,有
成立,即线性时变孤立子系统的零解是不稳定的,存在
时,则具有时滞的时变系数系统(2)的零解也是不稳定的。
今考虑具有时滞的线性大系统
(11)
或记为
(12)
与(11)有关的无时滞的时变系统为
(13)
对(13)的变系数矩阵
,按主对角线分解成
个孤立时变子系统为
(14)
其中
,
,
为
维时变矩阵。现在假设
连续有界可微,
(15)
其中
是与
无关的正数。
(16)
(17)
(18)
设(14)的特征方程为
(19)
又设(14)的特征方程(19)的所有特征根都具有负实部:
(20)
引理3:若系统(11)的系数连续有界可微,条件(15)、(16)成立,及线性时变子系统(14)的特征方程(19)的所有特征根据有负实部,存在
,使得
成立时,即线性时变孤立子系统(14)的零解也是渐近稳定的,存在
,使当
时,则具有时滞的线性时变大系统(11)的零解也是渐近稳定的。
当
时,得到
引理4:若系统(13)的系数连续有界可微,条件(15)、(16)成立及线性时变子系统(14)的特征方程(19)的一切特征根都具有负实部成立,存在
,使得
成立时,即线性时变子系统(14)的零解也是渐近稳定的。
今考虑
时具有时滞的非线性时变系统的稳定性
(21)
或记为
(22)
假定在域
中满足不等式
(23)
其中
是于
无关的正常量,并且在域
中,
对所有变元连续及使系统(22)对任何初值的解有唯一性条件成立。
引理5:设引理1的条件成立,即线性时变子系统(4)的零解是渐近稳定的,并设式(21)的非线性项满足条件式(23),存在
,使当
时,则具有时滞的非线性时变系统(22)的零解也是渐近稳定的。
引理6:设引理2的条件成立,即线性时变孤立子系统(4)的零解是不稳定的,并设(21)的非线性项满足条件(23),存在
,使当
成立时,则具有时滞的非线性时变系统(22)的零解也是不稳定的。
今考虑具有时滞的一般非线性时变大系统
(24)
或记为
(25)
假设在域
满足不等式
(26)
其中
是与
无关的正常量,并且在域
中,
对所有变元连续及使系统(22)对任何初值的解有唯一性条件成立。
引理7:设引理3的条件成立,即线性时变孤立子系统(14)的零解是渐近稳定的,并设(24)的非线性项满足条件(26),存在
,使当
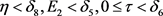
时,则具有时滞的非线性时变大系统(25)的零解也是渐近稳定的.
引理8:在引理7的条件下,若滞后
,当
时,则得到无滞后的非线性时变大系统的零解的稳定性。
引理9:在引理7的条件下,若
,当
,则得到具有时滞非线性定常大系统
的零解是渐近稳定的。
引理10:在引理7的条件下,若
,当 时,则得到非线性定常大系统
时,则得到非线性定常大系统
的零解是渐近稳定的。
3. 主要结果
3.1. 经济大系统模型
一个经济社会是有千千万万个商品组成的,这里的商品既包括消费品也包括劳动者的酬劳,凡是可以用价格衡量的,在此模型中,都是商品。这样,商品价格向量就是:
(27)
系统中每种商品都是相互联系的,任何一个商品的价格都是由其他商品的价格所决定的,至于如何影响,取决于线性系数矩阵
:
(28)
作为经济系统,必然有非线性因素存在,设为:
(29)
商品价格是时间
的函数,这样商品价格向量变为:
(30)
商品价格的线性系数矩阵变为:
(31)
在商品价格随时间变动的过程中,难以避免存在滞后性,所以设定一个滞后的商品价格矩阵:
(32)
同样地,非线性因素变为:
(33)
滞后商品价格空间的线性矩阵设为
:
 (34)
(34)
由以上8个设定,给出此类经济大系统的模型:
(35)
其中
(36)

(37)
3.2. 模型解释
是商品价格随时间的变化,在此经济系统中,时间
是唯一的参数,其他可能影响到商品价格的因素先忽略不计。
一个商品价格的变化除了和当即时刻
的价格有关,还具有时滞性,和
有关,所以,就存在
个时滞时刻:
(38)
所以对于此系统,可以合理地表示为:
(39)
根据定理7,可知此系统的零解是渐近稳定的。
4. Hopf分支
(40)
其中
和
都为常数。当
发生变化时,
在右半平面上的零点重数之和当且仅当有零根出现在虚轴上或穿过虚轴时才发生变化。
因为系统至少有一个实根,当
时,系统的正平衡点
出现Hopf分支。若模型满足假设条件时,则当
,正平衡点一致渐近稳定,而当
不稳定,并且在
附近出现分支。Hopf分支周期解稳定,周期解趋于一个稳定的极限环
表示时间滞后,即商品价格的时刻越接近当前时刻的间隔越小,越有利于整个经济大系统的稳定。