1. 引言
随着经济的发展,客户定制、个性化生产等商业模式在各行各业广泛出现,为了在全球竞争中占据优势,企业的生产活动更多地倾向于项目化运作 [1] 。项目资源调度主要解决如何在不同项目或不同工序间合理分配资源,对项目工期、成本等目标的实现至关重要。1963年,Kelley [2] 首次提出了资源受限项目调度问题(Resource-constrained project scheduling problem, RCPSP),并以项目完工时间最小化为目标函数。该问题已被证明为NP-hard问题。但世界上90%的项目都是在多项目并行的环境下实施的 [3] ,因此,资源受限多项目调度问题(Resource-constrained multi-project scheduling problem, RCMPSP)开始出现,Fendley [4] 首次在其研究中完整地描述了多项目资源调度问题,同时提出了设置项目优先规则、协调到期时间等调度方法。
以往的研究大多假设资源在不同项目间的转移不需要耗费任何时间和成本,这显然与实际情况不符。在现实中,特别是建筑工程项目,大型施工机械的转移对项目进度和成本的影响很大。针对这一缺陷,Kruger D [5] 首次在模型中引入了资源转移时间这一变量,并提出了相应的启发式算法。随后,宗砚 [6] 在其研究中同时考虑了资源转移时间和资源转移数量的约束,并提出了一种基于三级启发式规则解码的改进遗传算法对模型进行求解。郭云涛 [7] 针对考虑资源转移时间的多项目调度问题提出了一种改进的量子遗传算法,经过算例分析证明该算法与传统的遗传算法相比寻优能力更强、求解速度更快。另外,企业的内部和外部环境中均存在着大量的不确定因素,在项目实施过程中经常出现资源供应不及时、恶劣天气干扰等因素导致项目超期或成本超支。并且,大型工程项目往往具有独特性和一次性且相关历史数据非常缺乏,这导致我们很难应用概率理论对不确定因素进行刻画。1979年,Prade [8] 首次在一个课程调度问题中应用了模糊集理论,他将课程持续时间作为模糊数,建立了相应的模糊调度模型并进行了求解,在弥补概率理论刻画不确定因素不足的同时,也为模糊理论在项目调度问题中的应用开辟了先河。后来,国内外学者开始利用模糊理论,对不确定环境下的项目调度问题进行研究。孙若昕 [9] 以项目完工时间最小化为目标函数、各工序单位时间内的资源需求量为模糊变量,建立了模糊资源受限多项目调度模型,并设计了相应的模糊优先规则,采用启发式算法对模型进行了求解。
尽管目前已经有少量学者在资源受限多项目调度问题中考虑了资源转移时间这一变量,但仍然缺乏对资源转移成本的考量,同时对不确定因素的研究较少。因此,本文提出了考虑资源转移成本的模糊资源受限多项目调度问题(Fuzzy Resource-Constrained Multi-Project Scheduling Problem With Resource Transfer Cost),在模型中同时考虑了资源的转移时间和成本,以多项目整体的资源转移成本和延期惩罚(或奖励)之和最小化为目标函数,并引入了模糊理论来刻画项目调度过程中的不确定因素,用三角模糊数表示资源转移时间和工序持续时间,使模型进一步接近实际项目环境。针对求解模糊多项目调度模型的需要,设计了相应的模糊优先规则,通过遗传算法对模型进行了求解。
2. 考虑资源转移成本的模糊资源受限多项目调度问题
2.1. 问题描述
在考虑资源转移成本的模糊资源受限多项目调度问题中,我们假设多项目调度问题由m个项目构成,其中项目p包括
个实工序和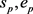 两个虚拟开始工序和虚拟结束工序,多项目问题除包含所有单项目的工序外,还包含整体的虚拟开始工序和虚拟结束工序。工序间的紧前关系约束可以由一个活动节点网络图来表示,除了多项目整体的虚拟开始工序和虚拟结束工序外,工序间的紧前关系约束仅存在于各个单项目内部,不存在于不同项目间。在调度过程中,我们对所有工序进行重新编号,工序1为多项目整体的虚拟开始工序,工序n为多项目整体的虚拟结束工序。虚拟工序
和
可以理解为资源池,调度开始前所有资源储存在
,调度完成后所有资源转移至
,且转移时间均为0。各个项目的合同时间主要以项目的关键链为基础,并由专家讨论决定。资源转移时间和工序持续时间均为三角模糊数,资源r从工序i转移到工序j所需的时间
,
分别表示可能的最短传递时间、最可能的传递时间和可能的最长传递时间,工序的持续时间
,
分别表示可能的最短持续时间、最可能的持续时间和可能的最长持续时间。
和
由项目相关专家进行讨论给出。
两个虚拟开始工序和虚拟结束工序,多项目问题除包含所有单项目的工序外,还包含整体的虚拟开始工序和虚拟结束工序。工序间的紧前关系约束可以由一个活动节点网络图来表示,除了多项目整体的虚拟开始工序和虚拟结束工序外,工序间的紧前关系约束仅存在于各个单项目内部,不存在于不同项目间。在调度过程中,我们对所有工序进行重新编号,工序1为多项目整体的虚拟开始工序,工序n为多项目整体的虚拟结束工序。虚拟工序
和
可以理解为资源池,调度开始前所有资源储存在
,调度完成后所有资源转移至
,且转移时间均为0。各个项目的合同时间主要以项目的关键链为基础,并由专家讨论决定。资源转移时间和工序持续时间均为三角模糊数,资源r从工序i转移到工序j所需的时间
,
分别表示可能的最短传递时间、最可能的传递时间和可能的最长传递时间,工序的持续时间
,
分别表示可能的最短持续时间、最可能的持续时间和可能的最长持续时间。
和
由项目相关专家进行讨论给出。
针对模型建立和求解的需要,我们做出如下假设:
1) 工序一旦开始不得被打断;
2) 所讨论的资源均为可更新资源,比如施工机械等,且工序所需资源必须从其他工序处转移,资源转移所需的时间
仅由工序i、工序j和资源r的类型决定,与资源转移数量无关。
3) 资源在同一项目内部转移不需要耗费时间和成本,仅在不同项目间转移需要耗费时间和成本,且转移时间
和转移成本
均满足三角不等式,即
,
。
2.2. 三角模糊数
模糊数的运算法则相较确定数有一定差别,我们以工序持续时间为例介绍三角模糊数的运算法则和比较方法,其中比较方法有多种,比如重心距离法、积分值法等,在本文中我们选取期望值法对三角模糊数进行比较。
(2-1)
(2-2)
(2-3)
(2-4)
(2-5)
(2-6)
(2-7)
(2-8)
(2-9)
(2-10)
(2-11)
我们假设
在区间
和
变动的概率相同,则通过隶属度函数推导可得
的期望为:
(2-12)
因此,我们以期望值为标准可得三角模糊数的排序规则如下:
1) 若
,则称
;
2) 若
,则称
;
3) 若
,则称
。
2.3. 数学模型
1) 模型相关符号及变量说明:
多项目调度问题的所有项目集合,
;
多项目调度问题整体的虚拟开始工序和虚拟结束工序;
项目p的虚拟开始工序和虚拟结束工序;
项目p的所有工序集合;
项目p的所有实工序集合, ;
;
多项目调度问题所有项目的工序集合,
;
多项目调度问题所有项目的实工序集合,
;
工序j的持续时间,
;
资源r从工序i转移到工序j所需的时间,
;
t,
时间索引,多项目调度问题工期的上界;
工序j的完工时间;
工序j的直接紧前工序集合,
,
,
;
工序j的直接和间接紧前工序集合;
工序j的直接紧后工序集合,
,
,
;
工序j的直接和间接紧后工序集合;
,
资源索引,多项目调度问题的所有资源集合;
资源r的数量;
工序j所需资源r的数量,
;
可以为任务j转移资源r的工序集合
;
工序j可以传递资源r的工序集合
;
项目p的合同期限;
项目p的单位拖期成本(或奖励);
资源r从工序i转移到工序j的单位成本;
无穷大的参数;
如果任务j在t时刻开始则为1,否则为0;
资源r从工序i转移到工序j的数量;
如果资源r从工序i转移到工序j则为1,否则为0;
2) 数学模型:
目标函数:
(2-13)
约束条件:
(2-14)
(2-15)
(2-16)
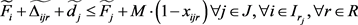 (2-17)
(2-17)
(2-18)
(2-19)
(2-20)
(2-21)
(2-22)
(2-23)
目标函数(2-13)为最小化多项目调度总成本,包括项目拖期惩罚(或奖励)成本和资源转移成本两部分;
约束条件(2-14)为任何工序只能在某一个时间点开始;
约束条件(2-15)为工序的完成时间与决策变量
的关系;
约束条件(2-16)为工序间的紧前关系约束,紧后任务只能在所有紧前任务完成后开始;
约束条件(2-17)为工序必须在所需资源到达后才可以开始;
约束条件(2-18)为某资源的转移数量和工序所需该资源数量的关系;
约束条件(2-19)为决策变量
和
的关系;
约束条件(2-20)为所有转入某工序的资源数量等于该工序所需的资源数量;
约束条件(2-21)为所有从某工序转出的资源数量等于该工序拥有的资源数量;
约束条件(2-22)为任何时刻所有任务所使用的资源数量不得超过资源的总供应量;
约束条件(2-23)为决策变量的可行域;
3. 基于模糊优先规则的遗传算法
3.1. 模糊优先规则
由于传统的优先规则无法适应模糊资源受限多项目调度模型求解的需求,因此本文在参考相关文献的基础上,设计了相应的模糊优先规则,表1为常见的模糊优先规则。

Table 1. Common fuzzy priority rules
表1. 常见的模糊优先规则
3.2. 遗传算法设计
本文选用遗传算法对考虑资源转移成本的模糊资源受限多项目调度模型进行求解,并针对求解需要对算法进行了部分改进,以下为算法的大致步骤。
1) 编码
本文参考多项目调度的活动节点网络图,设计了基于工序分层的编码方式,只有前一层中的工序执行完毕后,才可以开始执行后一层中的工序。具体规则为:a) 同一层中的工序不得有紧前关系约束;b) 前一层中的工序不得包含后一层中的紧后工序;c) 同一层中所有工序对某资源的需求量不得超过该资源的总量。
2) 解码
本文采用基于模糊优先规则的启发式调度方法对染色体进行解码,大概流程如下:a) 按照层级先后进行工序执行和资源分配;b) 同一层级中的工序按照模糊优先规则进行排序,并确定相应的资源转移工序和转移量,本文选用
工序最晚开始时间最小为模糊优先规则。
3) 适应值函数
为了便于模糊数的比较,本文以目标函数的期望值作为适应值函数。
4) 交叉和变异
本文选择常用的单点交叉法和对换变异。随机选择交叉点,子代的编码构成为交叉点前的遵循父代,交叉点后的在剔除已选取的编码的基础上遵循母代。变异的规则为,在前后两层直接无紧前关系约束的基础上,直接对换两层的编码。图1为基于模糊优先规则的遗传算法的流程。
4. 数值实验
本文给出了一个多项目资源调度的算例,由4个项目
、共18个实工序组成,如图2所示,项目
的合同工期分别为35、40、55、50,单位拖期惩罚(或奖励)分别为3、4、4、5。工序持续时间和资源转移时间均为三角模糊数,这4个项目共享3种可更新资源,资源总量分别为20、15、25,具体参数如表2和表3所示。
在具体调度过程中,采用前文中提到的模糊优先规则
对同一层中的工序进行排序,当遇到多个工序的最晚开始时间相同时,优先调度序号小的工序,另外,在程序运行时,设置了最大迭代次数为100代。最终求得模糊最优解为(139, 158,170),调度方案为(1, 2, 3, 4, 6, 7, 8, 5, 9, 11, 13, 10, 15, 14, 17, 16, 18)。

Figure 1. The flow of genetic algorithms based on fuzzy priority rules
图1. 基于模糊优先规则的遗传算法流程

Figure 2. The network diagram of multi-project scheduling examples
图2. 多项目调度算例网络图

Table 2. Relevant parameters of the example
表2. 算例相关参数
Continued

Table 3. Relevant parameters of the example
表3. 算例相关参数
Continued
5. 结论与展望
在建设工程领域,多项目共同进行已经非常普遍,资源如何合理调度对项目成败至关重要,不确定因素频发也往往导致项目超期或成本超支。本文在模型中考虑了可更新资源在不同项目间转移所带来的时间和成本的影响,并引入了三角模糊数来刻画项目实际调度过程中的不确定性。在弥补以往研究不足的同时,也使得调度模型更加贴近实际情况。在求解方面,本文采用了基于模糊优先规则的遗传算法,经过数值试验发现该算法可以很好求解同时考虑资源转移时间和成本的模糊资源受限多项目调度模型。
但是,本文在研究中仍存在不足之处,将在未来研究中继续深入探讨:其一,模型中只考虑了施工机械等可更新资源,在实际项目调度过程中,工程材料等不可更新资源的调度问题对项目成败同样重要;其二,本文采用三角模糊数来表示工序持续时间和资源转移时间,并未验证三角模糊数是否为对不确定因素最合理的刻画方式。