1. 引言
投资组合管理策略分为积极投资组合管理策略和消极投资组合管理策略,其中积极投资是指投资者通过主观行为,以追求最大收益或超越市场表现而做出投资管理的策略行为,通常情况下积极投资与投资风格、进出市场时机、行业以及股票的选择等相关。消极投资是一种只期望与市场指数取得相同的收益,而不超越市场指数的投资策略。
近年来随着基金管理越来越成熟,并且大多数的基金倾向于用指数化的方式进行投资,故而指数追踪必然是大部分投资者的选择。同时,随着市场管理制度的健全,想要在低于股票本身真实价值的价格买入股票的可行性越来越小,指数追踪正是完美解决这一困境的有效途径。
对指数追踪进行研究,这对我国资本市场甚至是国际资本市场,都有重要的实际意义和理论意义。研究者研究新的追踪方法,从而使得追踪误差更小,对于投资者而言就有着更便利而且多品种的投资选择,同时获得更高的投资回报。
在国外,最早提出投资组合理论的是Markowitz (1952) [1] ,该理论包含均值–方差模型和投资组合有效边界模型;Gilli和Kellezi (2002) [2] 提出了一种关于指数追踪的门限接受算法;Koenker和Bassett (1978) [3] 最早提出了分位数回归的概念;此后,学界开始对分位数回归的理论进行了深刻的研究,如Koenker和Bassett (1978) [4] 推导出了分位数回归系数的渐进分布;而Mezali和Beasley (2013) [5] 则提出用分位数回归来构建金融追踪组合。
在国内,沈双生和郭子忠(2003) [8] 全面的介绍了指数型基金具有的优势;范旭东(2006) [9] 通过比较分层抽样中的五种选股方法发现遗传算法在DMinMax模型下的效果最好;后来,杨国梁、赵社涛和徐成贤(2009) [10] 构建了基于支持向量机(SVM)的指数追踪模型,通过与Ruiz-Torrubiano (2009) [7] 的模型进行对比,证明了基于SVM的指数追踪模型有更好的效果;Baestaens (1994) [6] 首先用人工神经网络对指数追踪问题进行研究。
本文将会在第2节先对变量进行详细介绍;在第3节给出本文相对应的约束条件;第4节介绍非线性转换;第5节给出回归模型的建立,包括线性回归的指数追踪和分位数回归的指数追踪;第6节实证分析,分别对线性回归的指数追踪模型和分位数回归的指数追踪模型进行实例分析;第7节将总结全文,提出该方法的优缺点。
2. 变量介绍
我们需要观察N只股票在时间
的价格,以及所追踪的市场指数在相同时间段的表现。本文将从这N只股票中选出K (K < N)只股票构建一个投资组合来追踪所选择的市场指数。该投资组合的建立包括K只股票的选择,每只股票的购买数量或投资比例。
一般构建指数追踪模型涉及的变量:
,指数追踪组合中第i只股票的最小投资比例;
,指数追踪组合中第i只股票的最大投资比例;
,当前追踪组合中第i只股票的持有数量,若新建追踪组合,则
;
,第i只股票在t时刻的价格;
,所追踪的市场指数在t时刻的价格;
,所构建的追踪组合在t时刻的收益率,本文中
;
,所追踪的市场指数在t时刻的收益率,本文中
;
C,构建指数追踪的总资本,总资本等于指数追踪的总价格和交易费之和;
,卖出第i只股票所需要缴纳的经手费和证管费的比率;
,买入第i只股票所需要缴纳的经手费和证管费的比率;
,卖出第i只股票所需要缴纳的过户费的比率;
,买入第i只股票所需要缴纳的过户费的比率;
,在t时刻第i只股票能够卖出的最大数量;
,在t时刻第i只股票能够买入的最大数量;
,总交易费用在总资本中的最大占比,且
;
决策变量:
,新的指数追踪组合中第i只股票的持有数量;
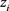 ,是一个0~1变量,
表示在新的指数追踪中有第i只股票,
表示在新的指数追踪中没有第i只股票;
,是一个0~1变量,
表示在新的指数追踪中有第i只股票,
表示在新的指数追踪中没有第i只股票;
,是一个0~1变量,
表示卖出第i只股票,
表示没卖出第i只股票;
,是一个0~1变量, 表示买入第i只股票,
表示没买入第i只股票;
表示买入第i只股票,
表示没买入第i只股票;
,表示第i只股票的卖出数量,
;
,表示第i只股票的买入数量,
;
为了更好的构建追踪组合,我们先做如下的假设条件:
1) 交易有成本。
2) 股票不能够卖空,即
。
3) 由于中国股市的股票是以一手(100股)为单位买卖的,因此
是以百为单位的一个数。
3. 约束条件
现在来考虑一下问题的约束条件,主要有:
(3.1)
(3.2)
(3.3)
(3.4)
(3.5)
(3.6)
(3.7)
(3.8)
(3.9)
(3.10)
(3.11)
(3.12)
(3.1)式是确保在新的指数追踪组合中只有K只股票;(3.2)式是确保如果第i只股票在新的追踪组合中(即
),那么它的持有量满足一个上下限,如果第i只股票不在新的追踪组合中(即
),那么它的持有量为0;(3.3)式表示经过重新调整之后第i只股票在新的追踪组合中的持有量;(3.4)式是确保在重新调整组合的过程中,第i只股票不会同时发生买入和卖出;(3.5)式是确保第i只股票的卖出量不超过
和
的最小值,如果没有卖出,那么
为0;(3.6)式确保第i只股票的买入量不超过
,如果没有买入,那么
为0;(3.7)式和(3.8)式则分别定义了第i只股票卖出和买入时所需要缴纳的过户费,由于上海证券中以6为首位数的股票都需要缴纳过户费,且每一千股缴1元,不足一千股按一千股计算;(3.9)式是一个平衡约束,即新的追踪组合的总价值等于总投资金额(当前追踪组合在T时刻的总价值加上现金变化,即C)减去总的交易费用;(3.10)式是对总交易费用设定一个适当的界限;(3.11)式定义连续变量
非负,(3.12)式定义
为0~1变量。
通常我们允许根据投资者的偏好来塑造指数追踪组合,包含的约束有:
① 公式(3.1)中K关系到追踪组合中股票种类数量;
② 公式(3.2)中
和
关系到第i只股票的最小和最大投资比例;
③ 公式(3.5)和公式(3.6)中
和
关系到第i只股票能够卖出和买入的最大数量;
④ 公式(3.10)中
关系到总交易费用在总投资额中的最大占比。
4. 非线性转换
新的追踪组合在t时刻时的总收益率为
,很显然,这是一个关于决策变量
的非线性
函数。为了线性化总收益率,我们借鉴了Beasley和Canakgoz (2008)的方法,假设它可以表示成单只股票收益的线性加权和,每只股票的权重表示了这只股票在追踪组合中所占的比例,且所有权重的总和为
1。假设所构建的追踪组合中的第i只股票在t时刻的所占权重为
,其中
,且
,那么追踪组合在t时刻的总收益为
。
通过
的表达式可以知道它仍是一个包含决策变量
的非线性表达式,对
进行一个恒定的变换,使得
不依赖于时间t,假设
进行变换后为
,那么
表示在T时刻第i只股票的所占比重。经过这个变换后,追踪组合在t时刻的总收益为
。但是
还是一个非线性表达式,我们
通过公式(3.9)对它进行替换:
(4.1)
又由公式(3.10)知道
的上界是
,因此我们可以对公式(3.13)继续进
行替换:
(4.2)
为了得到线性表达式,可以近似的估计
的值,即:
(4.3)
通过近似估计之后追踪组合的收益可以近似表达为
。
5. 回归模型建立
5.1. 基于线性回归的指数追踪
根据一元回归方程我们可以建立第i只股票的收益率与市场指数收益率的关系式:
其中
。从经济学上看
表示市场指数以外的部分对第i只股票收益的影响,
表示市场指数对第i只股票收益的影响。根据公式(4.3)可知在所构建的追踪组合中的每只股票所占权重分别为
,那么追踪组合在t时刻的总收益
为:
(5.1)
令
,
,那么公式(5.1)可以简写成
(5.2)
根据指数追踪的性质,我们希望公式(5.2)中的
,
,这样就能完全复制所追踪的市场指数。
通过最小二乘法可以得到
和
的估计值为
和
,那么
和
的估计值为
和
,且
,
。现在目标是使得
,
,下面我们将介绍一种方法来尽可能达到
这个目标。我们将求解如下问题:
(5.3)
其中w满足的约束条件为公式(3.1)~(3.12)和(4.3),并且
,
。
和
是由投资者自己决定的,如果投资者偏向于获得不受追踪指数影响的收益的话,可以给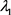 赋予更大的值;如果投资者偏向于更好的复制追踪指数的收益,可以给
赋予更大的值。
赋予更大的值;如果投资者偏向于更好的复制追踪指数的收益,可以给
赋予更大的值。
5.2. 基于分位数回归的指数追踪
5.2.1. 分位数回归参数估计
在线性回归中我们是通过最小二乘法解决优化问题从而估计系数
和
。在分位数回归中可以模仿线性回归构建一个优化问题:
(5.4)
其中
定义残差
,那么
分位数回归模型(5.4)的系数
和
的值由以下得出:
(5.5)
公式(5.5)中第一个式子是指正的残差之和(即
在回归线之上),第二个式子是指负的残差之和(即
在回归线之下)。这里正的残差得到的权重为q,负的残差得到的权重为1 − q,随着q的增大将有更少的正残差,那么对它赋予更大的权重,随着q的减少则会有更多的正残差,那么就对它赋予更小的权重。
而公式(5.5)是非线性的模型,需要将其转化为线性的模型才可以求解。,模仿3.2.2中使用的方法,引入变量
和
,分别代表正、负残差的绝对值,然后公式(5.5)可以转化为:
(5.6)
(5.7)
(5.8)
(5.9)
这就是一个线性规划问题,从而很容易解决并得到
和
的值。
5.2.2. 分位数回归模型建立
模仿5.1中用线性模型构建第i只股票的收益率与市场指数收益率的分位数回归关系式:
追踪组合在t时刻的总收益
为:
(5.10)
令
,
,那么公式(5.10)可以简写成
(5.11)
根据指数追踪的性质,我们希望公式(5.11)中的
,
,这样就能完全复制所追踪的市场指数。
通过5.2.1可以得到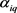 和
的估计值为
和
,那么
和
的估计值为
和
,且
,
。与5.1相同,目标是使得
,
,使用的方法也与5.1类似:
和
的估计值为
和
,那么
和
的估计值为
和
,且
,
。与5.1相同,目标是使得
,
,使用的方法也与5.1类似:
本文的目标是
,
,那么目标函数如下:
(5.12)
s.t. 公式(3.1)~(3.12),(4.3)
6. 实证分析
6.1. 基于线性回归的指数追踪模型的实证分析
我们分别考虑①
和
,②
和
,③
和
这三种情况。第①种情况指投资者十分看重风险,只想获得基础的收益;第②情况指投资者不考虑投资风险,只想得到跟目标指数相同的收益;第③种情况则是投资者对风险和收益同样看重。我们将会在每种情况下分别对K = 5,10,15进行分析。
1)
和
,我们得到如表1的结果。

Table 1. Tracking error table for different stock selections in the training set (1)
表1. 训练集中不同选股的跟踪误差表(1)
从表1中可以知道,最大权重选股法和最大市值选股法的追踪误差、最大偏差和最小偏差之间的差距都是随着K值的增加而减小的,且最大权重选股法的追踪误差比最大市值选股法的追踪误差减小的跨度更大,最大相关系数选股法得到的追踪误差、最大偏差和最小偏差之间的差距则都是随着K值的增加而变大。随着K值的增加,最大权重选股法所选的股票在上证50所占的权重越来越大,因此能够更好的拟合上证50。最大市值选股法跟最大权重选股法类似,因为上证50成分股的选取方法需要参考市值,且市值越大的越有可能所得到的权重越大,所以能够越来越好的拟合上证50。而最大相关系数选股法这是根据股票与上证50的走势相关程度选取的股票,也就是说所选出来的股票本身就跟上证50的走势非常相似,而
则只要求追踪组合注重收益,不注重走势,会出现随着K值的增加而变大的原因可能是前5只股票已经能够很好的拟合上证50,限于对单只股票的最小权重为0.01的约束,反而分散了之前的效果。
下面我们来看看在不同的选股方法下得到的
和
值,如表2所示:

Table 2. Table of coefficient values for different stock selections in the training set (1)
表2. 训练集中不同选股的系数值表(1)
从表2中可以看出,三种方法的
值都会随着K值的增大而减小,且并不非常接近于1,而
值的变化与K值的关系不明显,但大部分的
值都达到了10−13级别,几乎可以认为为零了。现在来分析一下出现这种情况的原因,由于第①种情况就是完全只考虑
,并且对
完全不考虑,也就相当于只考虑
,不考虑
,这就导致出现了之前说的现象。
为了更直观的知道追踪组合在训练集与上证50收益的对比,同时结合表1和表2,我们分别给出在K = 15时的最大权重选股法和K = 5时的最大相关系数选股法在训练集中得到的追踪组合和上证50收益的对比图。

Figure 1. Maximum weight picking method in the first case
图1. 第①情况下最大权重选股法

Figure 2. Maximum correlation coefficient picking method in the first case
图2. 第①情况下最大相关系数选股法
从图1、图2中我们可以看出这两种方法在所对应的K值下都可以很好的追踪上证50的收益。我们给出在这两种情况下追踪组合的表达式。
a) 最大权重选股法在K = 15时的追踪组合为:
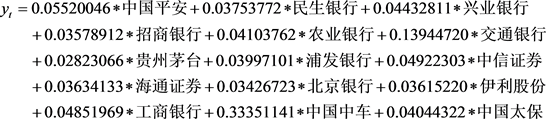 (6.1)
(6.1)
现在用该组合在测试集上进行测试,并与上证50进行比较,结果如图3所示:
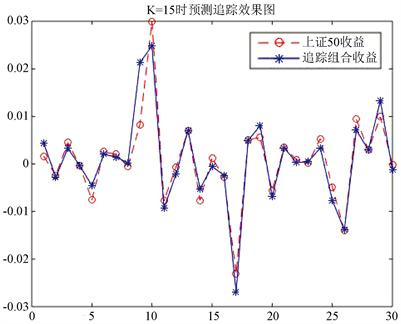
Figure 3. Prediction of the maximum weight stock picking method in the first case
图3. 第①情况下最大权重选股法预测图
此时的追踪误差(TE)为0.003067114107119,最大误差(MAXTD)为0.013027713614942,最小误差(MINTD)为−0.005054363525322,TTD的差距为0.018082077140264。从图3中看出,所构建的追踪组合对上证50的拟合效果很好。
b) 最大相关系数选股法在K = 5时的追踪组合为:
(6.2)
将模型运用在测试集上,求出结果,并与上证50进行对比,结果如图4所示:
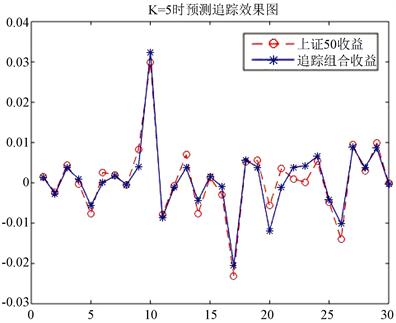
Figure 4. Prediction of the maximum coefficient stock selection method in the first case
图4. 第①情况下最大系数选股法预测图
有TE = 0.002436240507776,MAXTD = 0.004084423670680,MINTD = −0.006281093979794,TTD = 0.010365517650473,所以追踪效果比较理想。对比最大权重选股法所得到的各值,可以发现在第①情况下我们使用最大系数法得到的追踪组合(6.2)的追踪效果更好。
2)
和
。与第①情况的解答过程相似,得到不同选股方法在训练集中的结果,具体如表3:

Table 3. Tracking error tables for different stock selections in the training set (2)
表3. 训练集中不同选股的跟踪误差表(2)
从表3中可以看出,最大权重选股法的追踪误差、最大误差和最小误差之间的差距是随着K值的增加而减小的;最大市值选股法的追踪误差是随着K值的增加而变大,最大误差与最小误差之间的差距变化趋势不明显;最大相关系数选股法的追踪误差,最大误差和最小误差之间的差距的变化趋势均不明显,其中K = 10的追踪误差最小。但是总体上来看的话最大相关系数选股法是最好的,其次是最大市值选股法,最大权重选股法则最不好。接下来我们来看看不同选股方法下得到的
和
值,如表4所示:

Table 4. Table of coefficient values for different stock selections in the training set (2)
表4. 训练集中不同选股的系数值表(2)
从表4中可以看出,三种方法的
值都是在10−4~10−5级别,而
值都十分接近于1了,这是因为第②种情况是同样重视
和
的,即同等考虑
和
。且
值的变化只有最大权重法是随着K值的增加而变小,其他两种方法变化趋势不明显;而
值只有最大相关系数法是随着K值的增加而增加的,其他两种方法也不明显。
综合表3和表4,我们选取最大市值选股法在K = 10时与最大相关系数法在K = 15时的追踪组合,并分别做出它们在训练集与上证50收益的对比图。

Figure 5. Maximum market value selection in the second case
图5. 第②情况下最大市值选
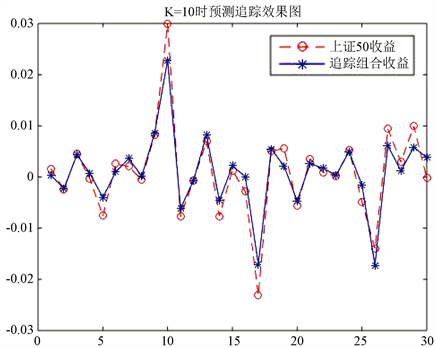
Figure 6. Maximum correlation coefficient stock selection method in the second case
图6. 第②情况下最大相关系数选股法
从图5和图6中可以看出追踪组合可以很好的追踪上证50的走势,虽然某些时候收益不如上证50,但是趋势基本相同。下面我们给出这两种选股方法在对应的K值下追踪组合的表达式。
a) 最大市值选股法在K = 10时的追踪组合为:
 (6.3)
(6.3)
用该追踪组合在测试集上进行测试并与上证50进行比较,结果如图7所示:

Figure 7. Forecast of the largest market value stock picking method in the second case
图7. 第②情况下最大市值选股法预测图
有TE = 0.002654323796411,MAXTD = 0.006012923913141,MINTD = -0.007081818650823,TTD = 0.013094742563964,预测的效果还是不错的。
b) 最大相关系数选股法在K = 15时的追踪组合为:
(6.4)
将该追踪组合的模型在测试集上进行测试并与上证50进行比较,如图8所示:

Figure 8. Prediction of the maximum correlation coefficient stock picking method in the second case
图8. 第②情况下最大相关系数选股法预测图
且有TE = 0.002719254704326,MAXTD = 0.006396698582851,MINTD = −0.007275034013586,TTD = 0.013671732596436,与最大市值法的预测结果相对比略有不足。
3)
和
通过不同的选股方法,得到了如表5的追踪误差表:

Table 5. Tracking error tables for different stock selections in the training set (3)
表5. 训练集中不同选股的跟踪误差表(3)
表5告诉了我们最大权重选股法的追踪误差、最大误差和最小误差直接的差距随着K值的增加而减小;最大市值选股法和最大相关系数选股法的这两个值变化与K值的关系不明确,其中最大市值法在K = 5时各值都为最小,而最大相关系数法在K = 10时追踪误差最小。但是总体上来看的话,最大相关系数选股法是优于其余两种选股法的。下面来讨论一下各方法得到的
和
值,如表6所示。

Table 6. Table of coefficient values for different stock selections in the training set (3)
表6. 训练集中不同选股的系数值表(3)
从表6可以看出,所有的
值都是非常接近于1,而
都是在10−4~10−5级别上的,这显然是因为第③情况导致的。第③情况是只重视
,而不关心
,所以会出现如此情况。但是和表4对比,两者差距并不大。也就是说,只要对
的重视程度达到了一半以上,那么模型的
值都会非常接近1。因此我们选择最大市值选股法在K = 10时与最大相关系数法在K = 10时构建追踪组合,此刻省略它们在训练集上与上证50的对比图。下面分别给出它们所构建的追踪组合的具体表达式。
a) 最大市值选股法在K = 10时的追踪组合为:
(6.5)
用该组合在测试集上进行预测,将得到的结果与上证50进行比较,如图9所示。
有TE = 0.002659695694857,MINTD = −0.007891735554979,MAXTD = 0.006239609992775,TTD = 0.014131345547754,预测的追踪效果接近第②情况下最大市值选股法预测效果,也是较好的。
b) 最大相关系数选股法在K = 10时的追踪组合为:
将该追踪组合的模型在测试集上进行测试并与上证50进行比较,如图10所示。
且TE = 0.002416360442177,MAXTD = 0.005831475971354,MINTD = −0.006883036973713,TTD = 0.012714512945067,略好于最大市值法。

Figure 9. Forecast of the largest market value stock picking method in the third case
图9. 第③情况下最大市值选股法预测图

Figure 10. Prediction of the maximum correlation coefficient stock picking method in the third case
图10. 第③情况下最大相关系数选股法预测图
6.2. 基于分位数回归的指数追踪模型的实证分析
为了让读者更清晰的感受到不同的q值对模型拟合的影响,本文选取了分位数
三个值,并将模型在训练集中的拟合结果根据选股法的不同而分别放在一起。
从表7~9可以看出,三种选股方法在相同的股票组合时,在q,K不变时,而
和
变化,此时各拟合结果的变化情况较小;在K、
和
保持不变时,q增大,TE和TTD的变化不明显,但是
和
的值变化还是比较明显的;当然,当q、
和
不变时,只有K变化时,各拟合结果的变化也较大。
基于分位数回归的指数追踪模型的拟合效果是不如基于线性回归的指数追踪的拟合效果的,甚至可以说差距挺大。最大权重选股法和最大市值选股法的训练集内的追踪误差大致在0.01~0.016之间,TTD更是高达0.08,同时
的值大多数都在10−1级别,远不如4.3节的10−4~10−5级别。因此,本节不给出在测试集中的拟合结果。

Table 7. Fitting results of the maximum weight stock selection method in the training set
表7. 训练集中最大权重选股法的拟合结果


Table 8. Fitting results of the largest market value picking method in the training set
表8. 训练集中最大市值选股法的拟合结果


Table 9. Fitting results of the maximum correlation coefficient stock selection method in the training set
表9. 训练集中最大相关系数选股法的拟合结果
7. 结论
本文主要是通过最大权重选股法、最大市值选股法和最大相关系数选股法来选出构建追踪组合的样本股,并且分别构建了基于线性回归和分位数回归的指数追踪模型。基于所构建的指数追踪模型通过选取不同的K值来对上证50指数进行了实证分析,得到了基于线性回归的指数追踪的效果比基于分位数回归的指数追踪的效果好这一结论,同时发现在不同的选股方法下,K值的增大对指数追踪的影响并不相同。
本文考虑了不同的选股方法对同一模型的影响,也考虑了同一种选股方法在不同的模型下结果的差距,更考虑了在同一选股法、同一模型下K值不同的影响,并对这些情况都进行了详细分析。在同一模型下,通过最大相关系数选股法得到的追踪组合的追踪效果整体上最好;在同一选股法下,基于线性回归的指数追踪模型的效果较好;在同一选股法、同一模型下,K值的变化对模型结果的影响并不相同,有的是随着K值的变大而效果更好,有的则相反。
在第6节中基于分位数回归的追踪模型的效果并不十分理想,这可能是由下面几个原因造成的:1) 2016年上半年的数据本身就线性性质明显,并没有太多极端值;2) 选股方法的局限;3) 计算分位数回归系数的程序迭代次数不够。
在未来,可以从以下几方面进行改进:1) 通过机器学习的方法进行选股,并且与前文的结果进行对比;2) 对于分位数系数估计的程序增加迭代次数。
基金项目
本文受云南财经大学研究生创新基金项目(2018YUFEYC035)等资助。