基于CFD的微孔空气静压轴承节流性能仿真分析

Simulation and Analysis of Throttle Performance of Microporous Aerostatic Bearing Based on CFD

摘要: 为了研究微节流孔对于空气静压轴承的节流性能的影响；本文利用CFD流体计算软件对微孔空气静压轴承的三维内部流场进行了数值模拟与计算分析；其中采用网格划分软件对轴承气膜网格进行划分，利用(Realizable K-ε)湍流计算模型分析气膜的流场特性；通过对微孔空气静压轴承的节流性能分析，研究了微孔空气静压轴承的节流孔直径对于轴承气膜内的压力及速度分布的影响，并给出了相应的对比结果；同时，将微孔空气静压轴承流场与传统节流孔空气静压轴承流场的不同区域的压力分布进行了对比，并分析了微孔节流与传统小孔节流流场之间的特点与区别。结果表明，在气膜承载面上，节流孔附近的压力降随着节流孔直径的增大，压力降呈先增大后减小的趋势；在节流孔中心线上压力随节流孔直径的增大，压力变化越不明显；微孔节流空气静压轴承与传统小孔空气静压轴承相比，在气膜承载面上，压力骤降小于传统小孔节流轴承，在节流孔中心线上，压力变化幅度大于小孔节流轴承。

Abstract: This paper is proposed to study the effect of micro-orifice on throttling performance of aerostatic bearings. In this paper, CFD computational software is used to simulate and analyze the three-dimensional internal flow field of the aerostatic thrust bearing with micro throttle holes. Meshing software is used to mesh the geometry. Realizable K-ε viscous model is used to analyze the flow field inside the film. Through throttling performance analysis of micro-porous aerostatic bearing, the influence of diameters of throttle holes on the pressure and velocity distribution inside the bearing air films is studied. The pressure distribution in different regions of the flow field of micro-hole aerostatic bearing is compared with that of traditional orifice aerostatic bearing, and the characteristics and differences between micro-hole throttling and traditional orifice throttling are analyzed. The results show that the maximum pressure drop near the outlet of the throttle holes on the bearing face increase first and then decrease as the diameter of the throttle holes increase. The pressure change along the center line of throttle holes becomes less obvious as the diameters of throttle holes increase. The pressure drop on the bearing face of aerostatic bearing with micro throttle holes is less than that of traditional aerostatic bearing. The pressure change on the centerline of the throttle holes of aerostatic bearing with micro throttle holes is larger than that of traditional aerostatic bearing.

1. 引言

空气静压轴承是以压缩空气为润滑介质的一种轴承，通过高压气体使轴承本体与承载面实现分离，可以达到减小摩擦和提供润滑的目的，所以其具有无摩擦，运动精度高的优点 [1] [2] 。

通过计算流体力学的方法对空气静压轴承内气膜的流场进行分析，是对空气静压轴承性能分析的重要手段；国内外学者，对于轴承的节流性能都有了许多研究成果，范酬 [3] 通过求解纳维斯托克斯方程结合压力以及马赫数的分布规律，分析了小孔(直径0.2 mm)气体静压轴承的静态特性和节流孔附近的流场变化情况；Masaaki Miyatake [4] 通过CFD计算微孔气体静压轴承微孔(孔径0.03 mm，0.05 mm)处的流量系数并利用有限差分法(FDM)研究其静态与动态性能，包括静刚度，动刚度和对应的阻尼系数；Uichiro Nishio [5] 利用计算流体力学(CFD)软件分析了进气孔直径小于0.05 mm的气体静压环形止推轴承的流量系数，并通过实验和数值分析对其静态和动态特性进行了研究。赵晓龙 [6] 利用CFD软件分析了小孔节流(直径0.2 mm)空气静压轴承内部流场随气膜间隙的变化关系，并研究了轴承气膜内部不同气膜高度气体的流速变化关系；姚娟 [7] 分析了小孔节流(0.16 mm)空气静压径向轴承节流气腔直径和气腔深度对轴承承载力的影响规律。Siyu Gao [8] 采用CFD软件分析了不同气腔形状对气体静压止推轴承的影响(供气孔直径0.15 mm)，并通过实验分析研究了不同气腔形状下轴承的承载性能。崔海龙 [9] 采用静态数值模拟方法获取了设计参数(小孔直径0.15 mm，0.2 mm)对承载力和刚度的影响规律，并分析了其内部流场的变化规律。

以上研究成果表明，目前，对于空气静压轴承的性能及其流场特性的研究方面，节流孔孔径大多处于0.2~0.4 mm的范围，且对于空气静压轴承的分析大多关注与轴承反映出的宏观性能。随着激光打孔和微钻头技术的普及，已可以通过加工得到尺寸更小的微孔(直径0.05 mm)，且由于这种微孔(小于0.1 mm)的孔径和气膜间隙已经达到相同的数量级，导致微孔气体静压轴承内部流场状况以及性能有别于有较大孔径的一般小孔节流空气静压轴承；同时，随着计算流体力学的迅速发展，可以利用CFD软件实现轴承内部流场的可视化，弥补实际试验的中存在的困难，所以可以通过CFD软件分析轴承的节流孔直径变化对流场的影响，从而直观分析其内部流场的情况。

所以本文建立了不同孔径下轴承的三维模型，采用CFD软件对模型进行有限元计算，通过求解纳维斯托克斯方程，研究对比不同孔径的微孔气体静压轴承内部流场情况以及节流孔内部和轴承承载底面上压力分布情况，并且将微孔静压轴承的内部压力分布与一般小孔节流气体静压轴承的压力分析进行对比，分析了微孔节流空气静压轴承的节流特点。

2. 基本方程

计算流体力学的基本方程为纳维斯托克斯方程，其为描述不可压缩流体粘度的基本方程，通过纳维斯托克斯方程可以推导出的质量守恒方程(1)，动量守恒方程(2)以及能量守恒方程(3)可被应用在可压缩，稳态计算流体的状况下：

$\frac{\partial p}{\partial x_i}\left(\rho {\mu }_i\right)=0$ (1)

$\frac{\partial p}{\partial x_i}\left(\rho {\mu }_i{\mu }_j\right)=\frac{\partial \left(p\right)}{\partial x_i}+\frac{\partial \left(p\right)}{\partial x_j}$ (2)

$\frac{\partial p}{\partial x_i}\left(\rho h{\mu }_j\right)=\frac{\partial \left(p{\mu }_i\right)}{\partial x_i}+{\tau }_{ij}\frac{\partial {\mu }_i}{\partial x_j}$ (3)

其中 $p$ 代表沿着坐标位置变化的压力， $\rho$ 代表空气的密度， $h$ 为轴承气膜间隙的高度， ${\mu }_{ij}$ 代表在笛卡尔坐标系中的速度方向， $x_i$ 和 $x_j$ 是代表在坐标系中的方向向量， ${\sigma }_{ij}$ 是粘性应力张量。

${\tau }_{ij}=\left[\eta \left(\frac{\partial {\mu }_i}{\partial x_j}+\frac{\partial {\mu }_j}{\partial x_i}\right)\right]-\frac{2}{3}\eta \frac{\partial {\mu }_i}{\partial x_i}{\sigma }_{ij}$ (4)

其中 $\eta$ 代表空气的动力粘度系数。

运用质量守恒方程和能量守恒方程，可以有效地保证在气膜内部的质量守恒，同时利用守恒方程可以有效地加强计算结果的平滑性与连续性。

3. 建立模型

通过初步分析，节流孔出口处存在压力骤降的现象，但在距离节流孔中心约0.2 mm处已经完成回升，并且由于在网格生成中，气膜间隙的厚度为20 um，若与轴承半径差异较大，则会导致网格质量降低，因此选择承载面直径为0.4 mm的节流区域建模并进行研究分析。本文利用Solidworks建立微孔及小孔空气静压轴承节流区域的三维模型，模型如图1所示，基本结构参数如表1。

4. 网格划分及边界条件

在建立完模型后对模型进行网格划分，由于气膜区域内的间隙很小，微孔孔径也很小，所以整个网格的扭曲率较大；同时由于在节流孔出存在结构变化较大的区域，因此导致流场变化也很大，为了整体上达到一个较好的网格质量，使CFD软件求解计算中更加容易收敛，需要在靠近小孔或微孔出口处流速较大的区域进行网格加密，网格如图2所示。具体网格建立过程如下，首先用MESH中的尺寸功能设置节流孔入口处与出口处承载面接触的圆形边上网格的数目为100个，接着在节流孔外表面上使用映射面网格划分(Mapped Face Meshing)，然后选在气膜间隙上表面进行细化(refinement)，最后选择气膜出口面设定尺寸(Sizing)，此处设置最小网格尺寸为0.005 mm。

Table 1. Three-dimensional model parameters of throttle zone of bearing

表1. 轴承节流区域三维模型参数

Figure 1. 3-D model of throttle zone of bearing

图1. 轴承节流区域三维模型

Figure 2. Bearing mesh and local mesh of throttle hole

图2. 轴承节流区域网格及节流孔局部网格

如图3为网格质量扭曲度分析结果，可见其skewness值大部分都位于0.8以下。在CFD软件分析的过程中质量差的网格会导致计算差异，对于一般计算skewness值要求小于0.8，通过上述的网格建立方法得到skewness值大多都位于0.8以下，且网格大部分都位于0.5以下，表明网格质量处于较好的程度，通过对网格skewness值分析，可以说明网格质量符合了CFD软件的计算精度要求。

在研究微孔气体静压轴承流场特性时，将入口边界设定为进气压力边界条件(pressure inlet)，将出口边界设定为出口压力边界条件(pressure outlet)。入口边界设置在如图2所示的圆形凸台顶部，下底面为气膜承载面，其侧面设置为出口边界，同时定义气膜承载区域外表面及小孔的外表面为壁面(wall)。在运算中设置入口边界条件为0.5 MPa，压力出口条件为0.1 MPa，参考压力为0.1 MPa。气体密度为1.225 kg/m³，空气的动力学黏度为1.7894 × 10⁻⁵ kg/ms，整个分析过程没有热量的传递和化学变化。

Figure 3. Grid skewness value

图3. 网格skewness值

5. 求解计算

基于CFD对微孔或小孔静压气体轴承的模拟分析主要可以分为三个步骤：① 模型的建立与网格的生成；② 利用CFD软件进行求解计算；③ 对求解的结果进行后处理分析。

在计算中采用湍流模型(Realizable K-ɛ)进行计算分析，在稳态计算下选用SIMPLE算法进行压力与速度的耦合计算，为了在计算结果中获得更高的精度，采用了二阶迎风格式，运算中设置常温为工作温度。

6. 计算结果分析

在轴承的三维模型中取如图4所示的研究平面，其为轴承的中心剖面，并研究该平面上的压力分布情况与速度矢量变化。图5为在该平面轴承的速度矢量随着小孔直径的变化情况，从图中可以看出随着轴承的节流孔直径的变化，轴承的速度最大位置随着轴承半径增大呈逐步向右移的趋势；在节流孔直径为0.05 mm、0.06 mm和0.07 mm时，节流孔出口与气膜承载面的转折处的速度变化比与节流孔直径为0.2 mm时转折处的速度变化剧烈；且在图中的不同直径的节流孔出口转折处均存在速度骤变的现象，说明在此处压力有较大变化。

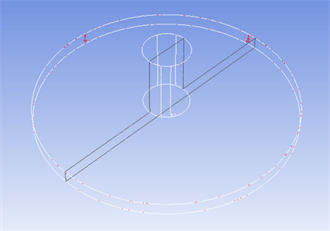
Figure 4. Bearing center position profile

图4. 轴承中心位置剖面

图6为轴承的中心剖面的压力分布随着小孔直径的变化情况，从图中可以看出随着轴承的节流孔直径的增大，高压区从节流孔出口底部呈逐步向节流孔孔中心移动，这种情况在小孔直径为0.2 mm时尤为明显；且在小孔出口转折处存在一定的低压区，此区域会导致轴承的压力分布出现压力骤降的现象；且随着轴承直径的增大，在小孔出口转折处的压力值越小。在图6中，为了对比不同孔径下的压力分布，设置压力分布显示范围为−0.01 Mpa~0.5 Mpa，而在轴承小孔直径为0.2 mm是，出现了节流孔出口压力小于−0.01 Mpa的压力，导致图6中出现了空白显示区域，所以在下图配图7，表示小孔直径为0.2 mm下轴承中心剖面的压力分布情况。

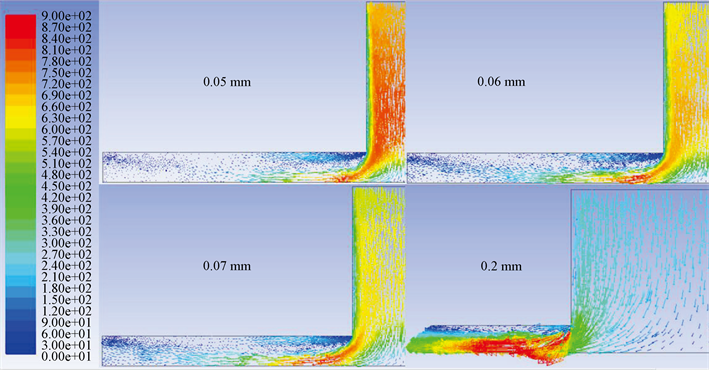
Figure 5. Velocity vector map of central section under different throttle hole diameters

图5. 不同节流孔直径下中心剖面速度矢量图

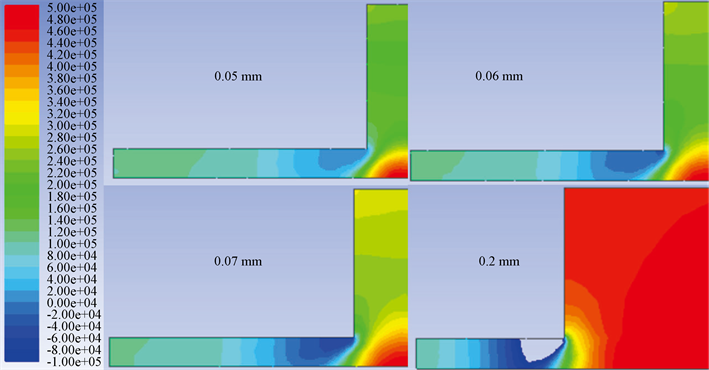
Figure 6. Pressure distribution in the central section with different throttle hole diameters

图6. 不同节流孔直径下中心剖面的压力分布

为了进一步研究微孔气体静压轴承承载面上的压力分布情况，如图8所示，取轴承承载底面中心线为压力分布研究线，并模拟计算这条线上的压力值；并分析了不同孔径空气静压轴承的压力分布情况。如图9所示为承载面中心线上的压力分布随着不同孔径变化情况对比，由图9可见，随着孔径逐渐变大，节流孔出口附近承载面上压力降低的幅度越大，随着孔径增大到0.2 mm时，压力骤降幅度出现了减小的趋势。如图10所示，为在不同孔径的压力骤降最大值，由图可见，压力骤降随着小孔直径的增大呈先增大后减小的趋势。

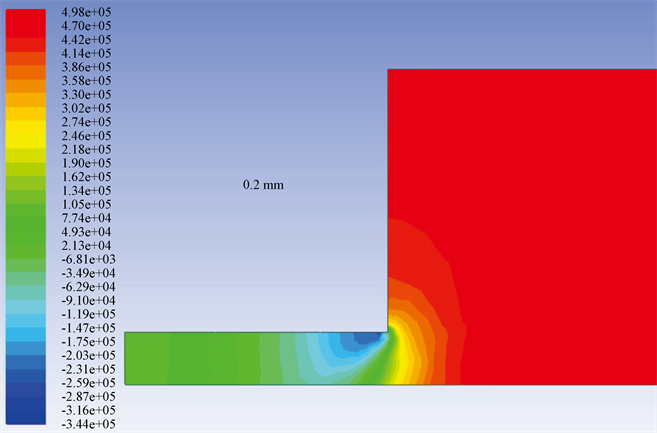
Figure 7. Pressure distribution in the center section of bearing with small hole diameter of 0.2 mm

图7. 节流孔直径为0.2 mm轴承中心剖面的压力分布

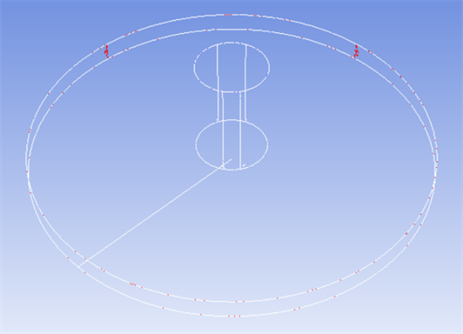
Figure 8. Pressure distribution line on bearing bottom bearing surface

图8. 轴承底部承载面上压力分布线

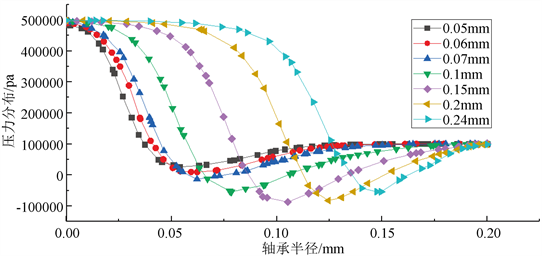
Figure 9. Pressure distribution on bearing bottom bearing surface with different throttle hole diameters

图9. 轴承不同节流孔直径底部承载面上压力分布

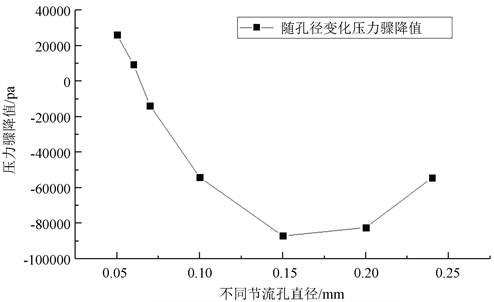
Figure 10. Chart of sudden pressure drop of bearing with throttle hole diameter

图10. 轴承压力骤降值随节流孔直径变化图

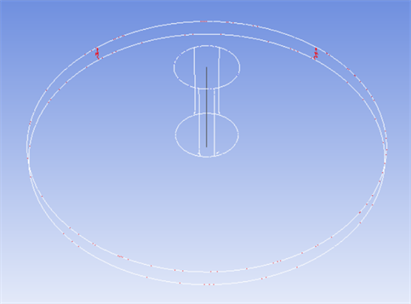
Figure 11. Center pressure distribution line of bearing throttle hole

图11. 轴承节流孔中心压力分布线

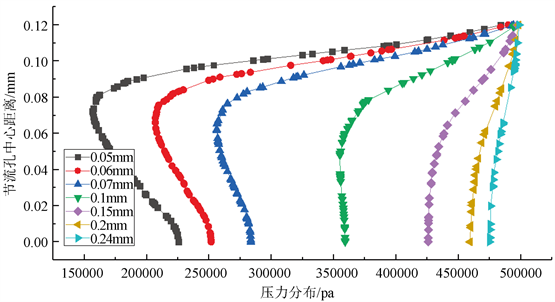
Figure 12. Pressure distribution on the center line of throttle hole with different throttle hole diameters

图12. 轴承不同节流孔直径节流孔中心线上压力分布

同时，本文进一步研究了进气孔内部的压力分布情况。如图11所示，在轴承节流孔内取一条竖直研究线，该线为节流孔的中心线，中心线从节流孔压力入口延伸至承载面底部。如图12所示，为不同节流孔孔径的轴承的节流孔中心线上的压力分布；由图12可见，随着孔径逐渐变大，节流孔中心线上压力值变化幅度逐渐变小；在小孔直径小于0.1 mm时，节流孔中心线上的压力变化幅度比节流孔直径大于0.1 mm的轴承变化幅度大。

7. 结论

1) 随着节流孔的孔径变大，节流孔出口的压力降呈先增大在减小的趋势。

2) 随着孔径逐渐变大，节流孔中心线上的压力值变化幅度逐渐变小，且供气孔入口的压力值越接近供气压力。

3) 微孔节流空气静压轴承在轴承底部承载面的压力骤降小于传统小孔供气空气静压轴承，在节流孔中心线的压力变化幅度大于传统小孔供气空气静压轴承。