1. 引言
太阳能光伏发电作为一种清洁、可再生、蕴藏量巨大的新能源,继风电之后逐渐得到人们的青睐,中国新增装机容量连续5年全球第一。而光伏的不确定性、间歇性和波动性导致光伏输出功率不稳定,从而改变系统潮流分布,对系统调峰、调频具有显著影响,造成光伏消纳困难的问题。2017年新疆阿克苏弃光量3.339亿千瓦时,弃光率高达36.07%,主要原因是对于光伏特性认识不足,导致电网调度策略不合理。因此,分析光伏出力在不同场景、不间空间尺度下的相关性特征具有重要意义 [1] [2] [3] 。
目前研究光伏电站相关性主要集中在太阳辐射度、地理位置、晴空指数等方面。文献 [4] 提出以距离为尺度,计算不同位置的2个光伏电站间实测地表水平面总辐照度与晴空地表水平面总辐照度比值的相关性。文献 [5] 在已知每月逐时晴空指数均值的前提下,从气象学的角度给出了逐时晴空指数的概率密度函数。文献 [6] 利用晴空指数来描述光伏电站出力的不确定性。文献 [7] 对影响光伏出力不确定性因素的云量进行了建模。文献 [8] 从概率分布、波动特性等方面研究了光伏出力遮挡因子的随机特性,并分析了光伏出力的空间相关性。文献 [9] 对新能源发电的相关性进行了研究,提出应用经验分布函数描述风力与光伏出力的随机性。文献 [10] 阐述了风电的聚集效应及空间相关性对风电随机特性的影响。文献 [11] 给出了不考虑延时和考虑延时的风电功率相关系数计算方法,并在此基础上提出了风电功率的平均风速相关性分析方法。文献 [12] 研究了光伏电站群相关性分析,提出从单一光伏电站扩展至电站群,同向波动逐渐减小,光伏功率波动逐渐减弱。上述文献侧重于分析光伏电站输入与输出相关性,未着重分析光伏电站输出与输出之间的相关性。
本文基于实测数据分析光伏电站数据的相关性。首先,给出了同一光伏电站不同时段出力的相关性和同一时段不同光伏电站出力的相关性计算方法;其次,从理论上分析云量因子和地理位置对于光伏电站出力相关性的影响;最后,选取新疆阿克苏光伏电站数据说明了云量因子和地理位置对同一光伏电站和不同光伏电站出力相关性的影响。本文研究光伏出力的相关性,为电网调度提供认识光伏特性的基础,有利于减少弃光率。
2. 光伏电站出力相关性的计算方法
2.1. 同一光伏电站不同时段出力
同一光伏电站不同时段出力相关性,反应的是某光伏电站一段时间的出力与另一段时间的出力之间的关系。对于具有L天实测数据的某光伏电站,假设该光伏电站第j天在第
时刻的实测出力为:
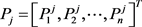 (1)
(1)
式中,n为光伏出力时长。
可获得反应同一光伏电站不同时段出力相关性的相关系数矩阵如下:
 (2)
(2)
(3)
式中,
表示L天同一光伏电站不同时段出力的相关系数矩阵,
表示第
天和第
天同一光伏电站不同时段出力的相关系数。
2.2. 同一时段不同光伏电站出力
同一时段不同光伏电站出力相关性,反应的是同一时段不同光伏电站出力之间的关系。
对于具有M个光伏电站的大型光伏基地,考虑延时T,则可获得考虑延时T的相关系数矩阵如下:
(4)
(5)
式中,
表示同一时段M个光伏电站出力的延时为T的相关系数矩阵,
表示同一时段第f号光伏电站和第g号光伏电站出力的延时为T的相关系数。
改变延时T的大小,即可得到同一时段不同光伏电站出力在不同延时情况下的相关性,从而更加准确的反映光伏电站出力之间的时空分布特性。
3. 光伏电站出力相关性的影响因素理论分析
光伏接收到的太阳辐射量的大小直接影响发电量,太阳辐射量越大,发电量越大。太阳辐射量大小与云量因子、地理位置有直接的关系。下文详细分析。
3.1. 云量因子
云量是指云遮蔽天空视野的成数,在气象上常以天空中出现的云量的多少计算天气晴朗的程度,云量因子表征云量对于光伏发电系统的输出功率影响程度,序列表示为
。正常情况下,晴天云量因子范围为
,多云天云量因子范围为
,阴天云量因子范围为
。
云量因子表现为光伏输出功率限制和波动,多云天和阴天的情况,输出功率小于晴天,波动频率大于晴天,因此光伏出力序列表现为输出功率大小限制、波动,以下分析云量因子对同一光伏电站不同时段出力相关性的影响。
假设光伏电站晴天的出力序列
:
(6)
假设同一光伏电站多云天的出力序列
:
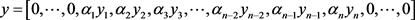 (7)
(7)
假设同一光伏电站阴天的出力序列
:
(8)
(9)
(10)
式(9) (10)表明,云量因子
、
、
数值会影响
、
之间的大小关系。
3.2. 地理位置
地理位置(纬度相同,经度不同)表现为同一出力时间,光伏开始、停止发电时间不同,光伏出力序列表现为开始、停止发电点向同一方向平移,以下分析地理位置对同一时段不同光伏电站出力相关性的影响。
假设参考光伏电站A的出力序列
:
(11)
假设同纬度不同经度、距离A光伏电站较近的光伏电站B的出力序列
:
(12)
假设同纬度不同经度、距离A光伏电站较远的光伏电站C的出力序列
:
(13)
假设条件1:在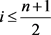 ,
,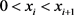 且
且
假设条件2:
(14)
(15)
根据假设条件2,可推导下式:
(16)
根据假设条件1,式(16)表明,
,即
。因此,开始、停止出力时间越接近的光伏电站,相关系数越大,进而说明在同一纬度上,地理位置越接近的光伏电站,出力相关性越强。
4. 实测数据光伏电站出力相关性分析
选取的光伏电站位于新疆阿克苏地区,太阳能资源丰富,年平均总辐射辐照度约160~200 W/m2,具体光伏电站信息如表1所示。光伏电站实测数据均来源于D5000自动采集数据系统,获取时间为2015年1月至12月,1分钟采集1次光伏出力值,1天共采集1440个数据值。

Table 1. Basic information of photovoltaic power station
表1. 光伏电站基本信息
4.1. 云量因子对相关性的影响
鉴于云量主要分为典型晴天、典型多云天、典型阴天,选取不同天气下嘉盛柯坪光伏电站数据,相应的天气如表2所示,对应的功率曲线如图1~3所示。两两分别做同一光伏电站不同时段出力的相关系数计算,比较分析云量因子对于同一光伏电站出力相关性的影响。
经相关系数计算可得表3,统计表3中数据可得表4,最值角度排序:
。
上述分析表明,晴天与晴天的相关系数的最小值大于除了晴天与多云天组合之外的任意组合的最大值,表明同一光伏电站出力相关性最强,原因在于两者的云量因子接近且干扰因素较小。

Table 3. Coefficient of correlation under different cloud cover
表3. 不同云量情况下的相关系数

Table 4. Correlation coefficient statistics
表4. 相关系数统计
4.2. 地理位置对相关性的影响
以表1中嘉盛柯坪光伏电站为参考电站,大唐阿克苏、正泰拜城、汉能新和、中节能轮台光伏电站作为比较电站,5个电站几乎在同一纬度,但处于不同经度。
选取参考电站和比较电站7月同1天数据,五个光伏电站功率曲线如图4~6所示,两两分别做同一时段不同光伏电站出力的相关系数计算,比较分析地理位置对于不同光伏电站出力相关性的影响。

Figure 4. Output curves of five power plants on sunny day
图4. 五个光伏电站晴天的功率曲线

Figure 5. Output curves of five power plants on cloudy day
图5. 五个光伏电站多云天的功率曲线
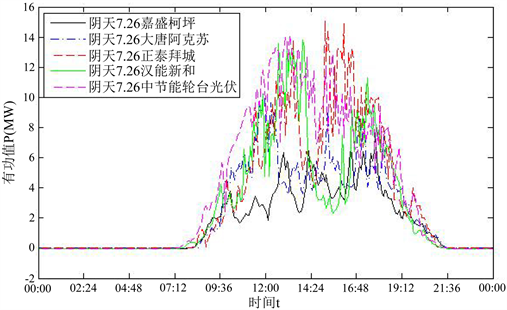
Figure 6. Output curves of five power plants on overcast day
图6. 五个光伏电站阴天的功率曲线
表5,图7~9表明,晴天和多云天情况下,比较电站与参考电站的距离越远,相关系数最大值所对应延时的绝对值越大。因此,由于参考电站的出力序列的起始点和终止点晚于比较电站,比较电站的出力序列只有经过延时,不同地理位置的光伏电站出力相关性才能达到最强。阴天情况下,相关系数最大值所对应延时的绝对值无明显规律,波动较频繁,原因在于受阴天影响,光伏出力随机性大。

Table 5. Coefficient of correlation and delay of geographical location considering delay
表5. 考虑延时的地理位置的相关系数及延时

Figure 7. Delay characteristics of sunny day
图7. 晴天的延时特性

Figure 8. Delay characteristics of cloudy day
图8. 多云天的延时特性
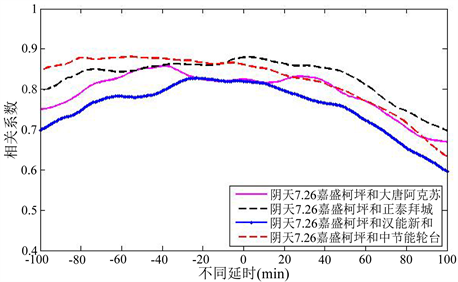
Figure 9. Delay characteristics of overcast day
图9. 阴天的延时特性
5. 结论
本文基于实测数据分析阿克苏光伏电站出力的相关性。首先给出了两种类型的光伏电站出力相关性计算方法,然后从理论上分析了云量因子和地理位置对于光伏电站出力相关性的影响,最后用实测数据分析光伏电站出力相关性。
1) 晴天与晴天的相关系数的最小值大于除了晴天与多云天组合之外的任意组合的最大值,表明同一光伏电站出力相关性最强,原因在于两者的云量因子接近且干扰因素较小。
2) 晴天和多云天情况下,参考电站的出力序列的起始点和终止点晚于比较电站,比较电站的出力序列只有经过延时,不同地理位置的光伏电站出力相关性才能达到最强。