1. 引言
一直以来,传染病的流行给人类造成了巨大的危害。天花、鼠疫、霍乱、艾滋病、非典、甲型H1N1流感、埃博拉等严重威胁到人类的生命和健康,导致社会倒退,给人类造成的损失大大超过历史上所有战争的总和。然而目前传染病的流行与防控形势仍然十分严峻 [1] [2] 。
人类免疫缺陷病毒(HIV)与常见传染病的传播特性具有显著的不同,例如HIV是不可治愈的,因此不存在治愈人群,且从感染到死亡期间都属于传染期,平均可长达十几年甚至几十年,病人在染病的不同时期病理反应也不相同 [3] [4] 。
世界卫生组织(WHO)给出了成年人感染HIV后的临床过程,主要包括三个阶段,如图1所示。
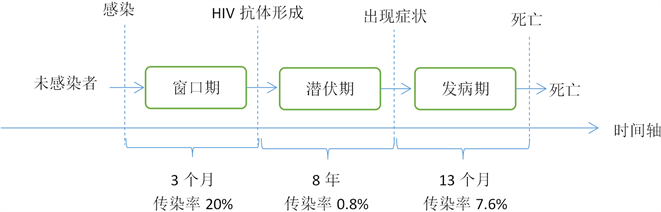
Figure 1. The clinical process of HIV infection in adults
图1. 成年人感染HIV后的临床过程
尽管在窗口期检测不到艾滋病病毒抗体,但艾滋病病毒已存在于感染者体内,并且可以通过HIV核酸检测证实,因此处于窗口期的感染者是具有传染性的。艾滋病潜伏期是指从感染艾滋病病毒到出现艾滋病症状和体征的时间,感染者在此阶段内也具有传染性。
2. 模型建立及预备结论
在建立模型之前,我们先做如下假设 [5] [6] :
1) 人口增加率为常数k,且均为易感者。
2) HIV携带者与易感者有相同的自然死亡率。
根据WHO公布的HIV的感染过程,将总人口
分为四类:易感者S、窗口期的HIV感染者
、潜伏期的HIV感染者
和发病期的HIV感染者
。采用双线性发生率,我们建立如下HIV传播模型:
(1)
其中
为人口增加率,
为人口自然死亡率,
为第i阶段传染率,
为第i阶段的平均间隔期。模型的初始条件如下:
(2)
下面根据模型的实际意义证明系统(1)满足初值条件(2)的解的存在唯一性、正性和有界性。
引理2.1:系统(1)满足初值条件(2)的解是存在且唯一的。
证明:系统(1)的右端函数是连续可微的,满足Liptstiz条件,因此满足初值条件的解存在且唯一。
引理2.2:若系统(1)满足初值条件(2),则它的任意一个解
对于所有的
都是正的。
证明:在给定的初始条件下易知系统的所有解都是正的。反之,假设存在时刻
,使得
,当
时
,其中
。若
,
当
,则由导数的定义知,
,而由(1)可知
,故矛盾,因此
对于
。
可类似讨论,引理得证。
引理2.3:若系统(1)满足初值条件(2),则它的任意一个解
对于所有的
都是有界的。
证明:由系统(1)可得:
解得
这里
是初始时刻人口总数。因此
易知
是系统(1)的正向不变集,且系统满足初值条件的解最终都进入
,即
是吸收集。由
的有界性可得解的有界性 [7] 。
3. 模型的无病平衡点和基本再生数
令
可得系统(1)的无病平衡点
。记
。下面我们用再生矩阵的方法 [8] [9] 求得基本再生数。
令
则系统(1)变成
,其中:
在
处的Jacobian矩阵分别为:
则模型的基本再生数
为:
定理3.1:当
时,无病平衡点
是不稳定的;当
时,无病平衡点
是局部渐近稳定的。
证明:系统(1)在
的Jacobian矩阵为:
记
易知
有一个特征值为
,
的其余三个特征值即为A的特征值。
当
时
。此时
必有一个正的特征根,因此无病平衡的
是不稳定的。下面说明当
时,
是局部渐近稳定的。
由前面分析知:
.
易知当
时
。另外A的第二加性复合矩阵 [10] [11] 为:
则
当
时
。因此无病平衡点
是局部渐近稳定的 [6] 。
事实上,
时
还是全局渐近稳定的。
定理3.2当
时,无病平衡点
是全局渐近稳定的。
证明:我们只需考虑
在系统的正向不变集
中的全局渐近稳定性。构造Lyapunov函数
如下:
其中
为待定常数。易知
且在
内V只在
取得最小值,即
。且有:
令
,则上式右端可变成:
因此当
时,
。又注意到
,由LaSalle不变原理,
时
在
上是渐近稳定的,而
为吸收集,因此
是全局渐近稳定的。
4. 地方病平衡点的存在性和渐近稳定性
这一节我们将讨论模型的地方病平衡点的存在性及其渐近稳定性。
定理4.1:当
时,系统(1)存在唯一的地方病平衡点。
证明:假设系统(1)有正平衡点
,则正平衡点
满足下列方程组:
且有
。则有如下关系成立:
因此,当
时存在地方病平衡点。
下面分析地方病平衡点的渐近稳定性。由于地方病平衡点的代数形式比较复杂,用特征值方法判断其局部渐近稳定性难以实现。我们用LaSalle不变原理证明地方病平衡点
在
上是渐近稳定的。
首先我们可以得到以下关于持久性的引理:
引理4.1若
,若初值条件满足
,则存在常数
使得满足初值条件的解有如下关系:
即从
出发的轨线不会趋于无病平衡点
。
定理4.1若
,则地方病平衡点
在
上是渐近稳定的。
证明:定义V函数:
其中
均为待定的非负常数。易知
且在
内V只在
取得最小值,即
。计算V沿系统的全导数,我们有:
(3)
为了简化符号,我们记:
注意到
的代数特征。假设(3)式右端形如:
其中
为待定常数。注意到
为系统(1)的平衡点,则有:
因此:
当且仅当
,即
。由LaSalle不变原理知地方病平衡点
在
上是渐近稳定的。
注:根据引理4.1和定理4.1,并结合引理2.3的证明,可知:地方病平衡点
还是全局渐近稳定的。
5. 数值模拟
为了验证理论结果的正确性,在本节中我们利用MATLAB对系统(1)的解进行数值模拟。取系统初值如下:
1) 当
时的情形
取参数值如下:
(4)
此时
,数值模拟结果如图2~图4所示。
由定理3.2可知,轨线最终收敛到无病平衡点
,由数值模拟得到
因此数值模拟结果与理论结果一致。
ii) 当
时的情形
取参数值如下:
(5)
此时
,模拟结果如图5~图7所示。

Figure 2. Three-dimensional projection of phase portrait of system (1) with
,
,
,
, and the parameter values are shown in (4)
图2. 参数取值如(4)所示,当初值取
时系统(1)的相图在三维空间的投影
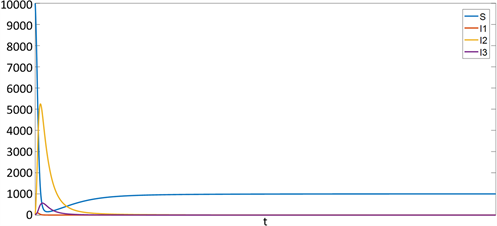
Figure 3. Images of
of the solution of system (1) with
,
,
,
and the parameter values are shown in(4)
图3. 参数取值如(4)所示,当初值取
时系统(1)的解各分量
随时间变化的图像
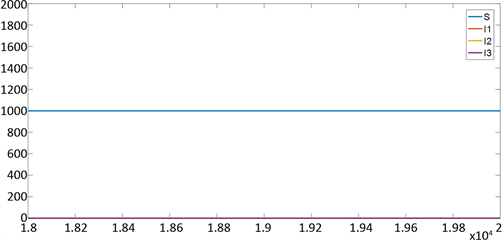
Figure 4. Images of
of the solution of system (1) with
,
,
,
and the parameter values are shown in (4), time of integration: [18000, 20000]
图4. 参数取值如(4)所示,当初值取
时系统(1)的解各分量
在时间
的图像
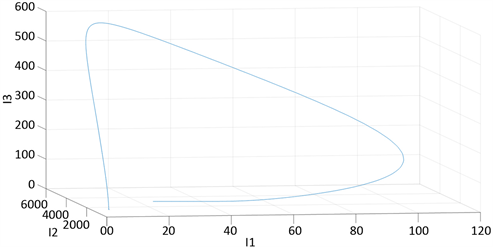
Figure 5. Three-dimensional projection of phase portrait of system (1) with
,
,
,
, and the parameter values are shown in (5)
图5. 参数取值如(5)所示,当初值取
时系统(1)的相图在三维空间的投影

Figure 6. Images of
of the solution of system (1) with
,
,
,
and the parameter values are shown in (5)
图6. 参数取值如(5)所示,当初值取
时,系统(1)的解各分量
随时间变化的图像
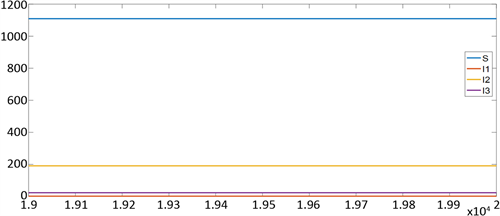
Figure 7. Images of
of the solution of system (1) with
,
,
,
and the parameter values are shown in (5), time of integration : [19000,20000]
图7. 参数取值如(5)所示,当初值取
时,系统(1)的解各分量
在时间
的图像
由定理4.1可知,任一正解最终将被吸引到地方病平衡点:
另一方面,由数值模拟得到:
这表明,数值模拟结果与理论结果吻合。
6. 结论
本文我们根据世界卫生组织给出的成年人感染HIV后的临床过程,建立了一个具有阶段结构和双线性发生率的HIV传播模型。通过对模型的稳定性分析我们知道,疾病本身的传播特征以及环境等因素会形成一个决定疾病最终消亡还是持续存在的阈值
:即当
时,疾病最终会消亡;当
时,会产生一个全局渐近稳定的地方病平衡点,即疾病最终会持续存在且稳定在该平衡点附近。数值模拟结果验证了理论结果的正确性。我们期望所得数学结果能为传染病预防与控制中心决策提供理论指导。
基金项目
受湖南省大学生研究性学习与创新性实验计划项目资助(湘教通[2016]283号)和长沙理工大学数学与应用数学专业“十三五”专业综合改革试点项目资助。
参考文献