1. 引言
目前,服务器制造行业中大部分企业都采用的是人工作业的仓库进行存储,存储的零部件种类繁多,数量庞大,体积差异明显,并且对存储条件有较高的要求,这些特点对零部件的货位分配及拣货作业提出了更高的要求,根据这些特点选择科进行合理的货位分配是提高仓库运作效率的关键。而目前大部分服务器制造企业在在分配货位方面做的都不够完善,其系统在分配货位时大多没有综合考虑零部件自身的特点以及周转率等、相关性等因素,这就使得了出入库时间长、相关货品存储距离较远,导致拣货效率低等问题,进而影响了生产效率。
当前关于货位优化模型的研究,主要有单目标货位优化模型和多目标货位优化模型两种。
Van [1] 在自动拣货系统的货位优化研究中,基于分类存储策略,以拣货时间最短为目标构建了单目标货位优化模型,并运用遗传算法进行求解,通过对拣货时间进行效果分析,验证了该方法有效的减少了拣货时间。罗键等 [2] 为了提高自动化立体仓库小车存取效率,以自动拣货小车拣货时间最短为目标函数,建立了单目标系统货位优化的数学模型,并基于离散粒子群算法实现了货位分配的优化,有效地缩短小车拣货时间。李珍萍 [3] 以人工拣选仓库或配送中心某一段时期内的历史订单为研究对象,建立了以人工订单拣选作业导致的人体能耗最小为目标的单目标货位优化模型,并利用贪婪算法对其进行快速求解,并验证了该方法能有效降低人工劳动强度,提高劳动效率。
Muppani [4] 将货物的存储空间与货物周转率的比值放入货位分配模型中,以存储和拣选成本最低建立模型,并运用遗传算法进行求解,并验证了优化后的货位分配结果比原货位分配方式更优。Mantel [5] 提出面向订单的货位指派方法,对一定周期的订单进行分析,在穿越拣选策略的条件下,考虑货品周转率和相关性,以拣货时间最短和同类物品距离最近为目标,将该问题抽象成线性整数规划模型,并用遗传算法求解上述模型。李霞 [6] 以自动化立体仓库为研究对象,对其货品的货位分配进行优化研究,考虑货架稳定性和出库频率,建立从入库、出库到倒库三个阶段的多目标动态货位优化模型,采用基于权重系数变换法的多目标遗传算法求解模型,并对仿真结果进行分析讨论,验证了算法的有效性。张子才 [7] 研究自动化仓库货位优化问题,提出了一种新的货位优化方法,综合考虑货物周转率及相关性因素,建立了多目标货位优化问题解析模型,并lingo优化工具进行了仿真分析。仿真分析结果表明,所提出的货位优化方案极大地提高了仓库的存储效率及存储利用率。郭有俊 [8] 根据电子元器件分销商区域配送中心的特点,运用聚类算法对元器件进行分析,并在此基础上构建了货位优化数学模型,运用贪婪算法进行求解,用实例证明优化后的储位分配方法可以以缩短拣货人员在货物拣取时的行走距离和作业时间,提高配送中心的作业效率。祖巧红 [9] 以立体仓库库存为研究对象,研究了货位分配优化问题。分析了汽车零部件货位布局优化原则,建立多目标货位分配优化数学模型,运用Matlab软件实现模型的求解,得出可行的货位优化方案。最后结合实例进行多目标货位优化数学模型求解及应用,并以三维仿真图形展示了优化效果,验证了所设计的遗传算法的有效性。夏云飞 [10] 以S企业零部件存储区为主要研究对象,对该公司的货分配问题,出货量以及出货频次为依据,运用EIQ分析法对零部件进行了ABC分类,优先将A类货品存放在离出库口较近的位置,B类其次,C类最后,从而使得整体出库时间达到最短。并以拣货时间最少,相关性大零部件距离最短、优化前后货物移动距离最小建立了多目标货位优化模型。并通过设计遗传算法多模型进行求解,对比了迭代前后货物距出入口的距离,证明了该方法的有效性。
无论是自动化立体仓库还是非自动化立体仓库,主要以拣货时间最短,货架稳定性最好,该作业能耗最低,相关性大的零部件离散度最小为目标,进行模型构建。单目标货位优化模型以其中一个为目标进行模型构建,多目标则考虑两个以上的目标进行建模。目前关于货位优化单目标及多目标数学模型的求解算法的研究较为丰富,主要有以下几种:遗传算法、改进的遗传算法、贪婪算法、嵌套分区算法、萤火虫算法、混合粒子群算法等,应用最广的是遗传算法。本文拟建立多目标货位优化模型,并运用遗传算法对A公司零部件仓库的货位分配进行优化。
2. 企业背景
A公司是一家大型生产企业,主要从事服务器及网络设备的生产制造,A公司零部件仓库占地约2000平方米,存储的零部件主要有IC类、PCB类、电容、电阻、连接器五大类,零部件种类繁多,数量庞大,体积差异明显。目前,A公司零部件仓库采用的是定位存储的存储策略,将五个大类零部件按照金额分为贵重物品、普通物品和低价物品三类,并将其分别存放在三个区域。仓库零部件以整箱的方式存放在4层搁板式货架上,经实地调查了解到仓库每个货架的长、宽、高分别为4 m × 1 m × 2 m,每个货架共有四层五列,共有货位26,000个,每个货位按照字母和数字的组合来编码。A公司零部件仓库布局见图1:

Figure 1. A company parts warehouse layout map
图1. A公司零部件仓库布局图
目前,零部件是纯人力拣货,采用摘果式拣货法进行作业,生产组根据生产计划在系统中提出物料领用需求,物料组的人审核需求,审核无误后打印出领料单交到仓管员手中,仓管员再把订单分配给拣货员,捡货员收到领料单上有计算机提供的货位信息,拣货员根据计算机的提示,把领料单上的零部件捡取出来,并且集中放到暂存区,等待运送到生产线上。A公司零部件仓库拣货作业流程见图2。
在货位分配方面,仓库各个区域的货位是拣货员根据经验进行分配的,仓库的出入库作业由捡货员手动完成。通过对仓库实地调研发现其在运作过程中存在拣货效率低、货架稳定性差的问题。对于拣货效率低的原因进行分析发现,导致该问题的主要原因有以下两点:首先,很多拣选频次高的零部件被存储在离出入库台较远的位置;其次,同一个领料单中的零部件相隔较远。对于货架稳定性差的原因进行分析发现,很多体积较大的零部件货位被分配在货架的高层,这样的货架整体重心就会偏高,使得货架稳定性差。
由此可见,导致拣选效率低、货架稳定性差的原因归根结底是货位分配不合理。因此,迫切需要对仓库进行货位优化,以实现仓库的高效运作。
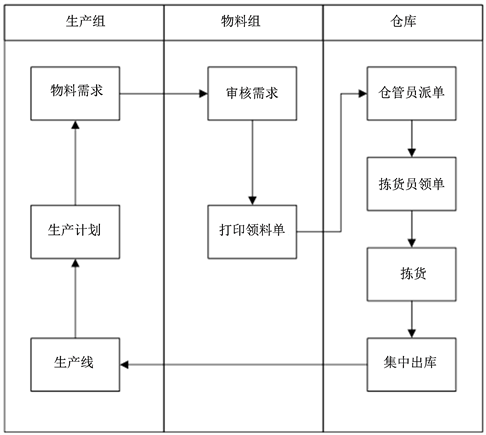
Figure 2. A company parts warehouse picking operation process
图2. A公司零部件仓库拣货作业流程
3. 多目标货位优化模型的构建
3.1. 模型假设及符号说明
3.1.1. 模型假设
在进行货位优化的实施过程中,应该考虑到一些客观的约束条件例如应该满足货位的数量、货位大小、货物尺寸等等这些条件。在本文的模型建立过程中,主要有以下约束条件:
1) 货位的数量都是固定的,不能超过原有的排、列、层数,当货物入库的时候,必须是在有货位的情况下,并且入库的货物应小于等于货位数。
2) 决策变量的限制,即货位坐标必须为整数。
3.1.2. 符号说明
根据A公司零部件仓库的实际情况,设仓库的货架总共具有X列、Y层、Z排,将存储位置为r列,s层,排t的货物记为(r, s, t) (
),记(0, 0, 0)为出库台的位置。记离出入口最近的为第一排,离出入库最近的一列为第一列,离地面最近的一层为第一层,每个货位的长、宽、高分别为L,W,H。模型中设计的其他参数如下:
1)
——零部件i到出入口的距离;
2)
——共有n种零部件;
3)
——货物i的周转率;
4)
——零部件i的质量;
5)
——设备与仓库地面的摩擦系数;
6)
——重力加速度;
7)
——零部件i所在的层数;
3.2. 模型构建
3.2.1. 目标函数的构建
本文研究的公司配送中心分拣区的货位优化问题属于人工作业的仓库,所以需要优化的目标是要提高工作效率,解决的是空间利用率,保证仓库货架的安全性。在进行货位优化主要追求的目标就是需要缩短作业时间,减少工作人员的能量消耗,提高空间利用率,提高货架的承受能力和稳定性。此外,从人工学的角度来考虑,货物的质量也对拣选作业的效率产生影响,人体耗能少,相应的工作效率会得到提高,所以,减少人体的能量消耗,对提高整个仓库的作业效率也是至关重要的。所以本文在时间目标、空间目标、安全目标的基础上,还考虑了人体耗能最小为目标,建立货位优化模型目标。
1) 要提高仓库拣货作业效率,应减短货物拣选时工作人员的行走距离。假设仓库有n件货物需要进行拣选操作,其中货物i的移动距离为横向、纵向和垂直距离之和那么最小化距离表达如下:
(1)
假设工作人员在拣选作业的时候速度是匀速行驶的,并且在x,y,z方向的速度分别是
,
,
,并假设
。拣选时间最优表达式为:
(2)
2) 为了提高空间利用率,对周转率高的货物,应该放置在离出入库较近的地方,综合以上两点,拣选时间最优的表达式如下:
(3)
3) 为了保证货架承载受力均勾,所有的货物进行放置的时候都需要考虑货位的承受能力,将重量大的货物放在下面,货物轻的放置在上面的原则来存放货物。货架的稳定性与重心密切相关,货架的重心越小,稳定性越高,所以构造目标函数,使得重心最小,表达如下:
(4)
4) 拣选作业的效率,还和人体的耗能息息相关,A公司仓库零部件的拣选作业中,基本都靠人工作业,所以人体的耗能最小也可以提高作业效率到达优化的目标。以人工拣选领料单作业导致人体耗能最小为目标,表达式如下:
(5)
3.2.2. 约束条件
该仓库共有z排货架,每排货架有x列y层货位,得到货位优化的空间约束条件为:
1)
2)
3)
其中r,s.t为整数。
4. 模型求解
4.1. 确定目标函数权重
求解多目标优化问题,一般情况下比较复杂。这是因为,多个目标同时获得最小值是比较困难的。所以有必要进行进一步的处理,使得多目标问题转化为单目标来求解,目前,已经有多种基于遗传算法的多目标求解方法,主要有权重系数变换法、排列选择法、并列选择法、混合法和共享函数法五种本文的思路是用权重系数变换法将多目标函数转化为单目标函数进行求解。
本文将上述几个目标函数赋予相应的权重系数分别为a,b,c,d,从而上述多目标优化问题就可以转化成单目标优化,各目标函数的线性加权表达式为:
(6)
权重的可以通过层次分析法来确定,层次分析法一般通过指数标度法来量化评价指标的重要性,就是通过设置不同的评价等级,如特别符合、一般符合、不太符合、不符合等不同维度进行对象重要性的等级评价。根据实际分析,指数标度法一般选取5个维度进行重要性分级,而当评价对象需要更加精准分析时,维度也可以适度扩展到9个。在确定评价对象的重要性权重后,对初始数据进行标准化、归一化、一致性分析等定量处理后,以此得到最优化的决策方案。1~9标度法如表1所示:
根据调查问卷得出时间、承受力、耗能的指标值如表2所示:

Table 2. Indicator value of each evaluation factor
表2. 各项评价因素的指标值
构造两两比较矩阵为:
求得a = 0.54;b = 0.28;c = 0.12;d = 0.06。
利用MATLAB求得该矩阵的最大特征值为4.12,故
,当n = 4时,查找平均随机一致性指标RI表可知RI = 0.9。故
,所以判断矩阵的一致性是可以接受的。所以权重a,b,c,d取值合理。
4.2. 遗传算法设计
1) 编码
编码分为货物编码和货位编码,遗传性算法不能直接处理参数,所以必须把它们转化为遗传空间的由基因按照一定结构组成的染色体或者个体,所以编码是一个转换的作用,不同的编码形式会影响到该算法求解问题的方向和影响交叉、选择和变异的运算方法。本文采用整数排练的编码方式。货物与货位的编码如下:
1) 一条染色体代表一种货位的分配方案;
2) 每条染色体中的基因数目就代表着货位优化区域内货物的个数;
3) 基因的值就代表货物存储的货位。
假设一个待优化的货位区域中有五件货物,第一件货物位于第一列、第二层、三排,即记做(1, 2, 3);第二件货位位于(2, 3, 4);第三件货物位于(3, 4, 5)第四件货物位于(4, 5, 6),;第五件货物位于(5, 6, 7)。故“123”、“234”、“345”、“456”、“567”表示染色体的一个基因,对应着每个货物,“123234345456567”表示一个货位的分配方案。
2) 确定使用度函数
用遗传性算法来求解多目标优化问题的时候,并不是直接求解目标函数,而是求解与目标函数有一定连带关系的适应度函数来进行求解。并且这里适应度的变化能反映目标函数值的变化,对适应度函数求解适应度值,适应度的大小能够判别达到或者接近最优解的程度。适应度的大小决定着个体遗传到下一代概率的高低,适应度大的遗传到下一代的概率高,反之,适应度低的遗传到下一代的概率低。货位优化是求多目标的最小值,将目标函数与个体的适应度进行转换的时候,目标函数越小,适应度相应的越大,这个个体遗传到下一代的概率就大,所以将多目标函数取倒数来作为模型的适应度函数。几个目标函数的取值范围是如果目标函数趋向于的时候,此时适应值会趋向无穷大,所以,为了防止此种现象的出现,需要将多目标函数加之后再取倒数。所以转换后的适应度函数如下所示:
(7)
3) 种群的初始化
种群规模的大小影响着对遗传算法的运算和结果。当种群规模较小的时候,得出的结果不具有代表性,优化性能差。当种群规模较大的时候,算法的计算过程复杂,但结果具有代表性,优化性能好。为了最大限度的保证种群的优良性和多样性。一般要求将种群G规模的大小设置在100到500之间。
4) 遗传优化算法的主要操作算子
① 选择操作
选择操作是通过判断个体适应度的大小,来确定父代中哪些能够遗传到下一代,哪有被淘汰。它最终的目的是通过优良基因来遗传产生新的个体,一代接一代迭代下去直到达到一个最优的结果。当种群
的规模为G,个体i的适应值为
,则个体被选中的概率为
,显然,适应度大的,被选中的
概率大,可以留下,而适应度小的,被选择到的概率低,则容易被淘汰。
② 交叉操作
交叉运算是将相互配对的染色体通过某种方式交换部分基因来产生新的个体,本文采用的是单点交叉算子。一般交叉概率的取值范围为(0.4, 0.99),显然,如果交叉概率过小,会使得很多个体不经过交叉进入了下代,阻碍了遗传进化的速度,而交叉概率过大,会破坏种群中的优良基因。本文选取的交叉概率是0.8。
③ 变异操作
变异操作就是为了保证种群的多样性防止出现过早的早熟现象而影响搜索能力,保证了遗传算法全局的搜索能力。本文采用的是基本位变异。一般的变异概率的取值范围为(0.001, 0.1),显然,和交叉变异类似,如果变异概率过大,会使得优良基因被破坏。而变异概率过小,则会陷入局部优化的概率会过大。本文选择的交叉概率为0.05。
4.3. 仿真实验
由于数据繁多,为了简化计算,这里就货位优化问题,有针对的选择一部分区域来进行货位优化,这里选取A公司零部件仓库货架区的20排货架作为研究对象,选取20个零部件为例,设定仿真的一些基本的参数,如表所示,假设遗传算法的初始种群的个数为100个,最大迭代次数设为50和150,交叉概率为0.8,变异概率0.01。参数值如表3所示:

Table 3. Simulation basic parameters
表3. 仿真基本参数
初始数据如表4所示:
利用遗传算法工具箱求解以上的货位优化问题,经过50次和150次迭代得到的结果如表5所示:
5. 结论
根据上述表格可得出,经过一定次数的迭代后,目标都得到了一定的优化,所以货位优化对于A公司零部件仓库提高作业效率,减少运营成本具有重大的意义。由此可见,根据一定的货位分配原则和货物存储策略对货位进行优化,在一定程度上对零部件仓库提升作业效率和降低运营成本起到重要的作用。
由上述对货位优化的结果进行分析可知,在经过具体的货位优化的时候,往往会由于仓库的规模较大而出现需要待优化货位过多的问题,经过对比分析,运用遗传算法可以有效的求解A公司货位优化的多目标组合模型,对于存在同样问题的企业具有借鉴意义。