1. 引言
开关磁阻电机(Switched Reluctance Motor, SRM)是一种双凸极结构电机 [1] ,因具有结构简单、成本低,可靠性高等优点,使其能够在恶劣、高速的环境中运行,这也使SRM具有广阔的应用前景。可因为SRM具有较大的转矩脉动,是它难以得到进一步的发展。近年来,不少专家学者将直接转矩控制应用于对SRM转矩抖振的抑制中 [2] [3] ,并取得了不错得控制效果。SRM的直接转矩控制系统一般采用双闭环结构,即外环为转速环,内环为磁链、转矩环,但由于转速环仍采用传统控制,所以控制系统仍存在鲁棒性差、超调量大等缺点。文献 [4] 将滑模控制引入SRM直接转矩控制的转速环中,使系统具有较好的鲁棒性。但传统的滑模控制本身就具有较大的抖振,为了能有效抑制抖振同时保留传统滑模控制的强鲁棒性,本文将引入高阶滑模控制。此外传统的直接转矩控制虽然对转矩脉动的抑制取得了一定的控制效果,但并不是十分理想。
因此,本文设计了基于Super-twisting滑模的转速控制器,并将其应用于直接转矩控制的双闭环调速系统中,此外对传统的直接转矩扇区进行近一步细分,并增加了相应的电压矢量。相比于普通直接转矩控制,该系统实现了快速响应,对转矩抖振也有明显的抑制效果,拥有较好的控制性能。
2. Super-twisting滑模控制器设计
一般来说,对于一个动态系统,通常有:
(1)
其中,u为控制输入量;
为状态变量;
为控制输出量;
为未知函数。
那么,对于式(1)的通用二阶滑模控制式为:
(2)
其中,
为符号函数;
为系统输出量;增益
、
为负值;
为指数调节因子。
由此可知,通过选择特定的增益可以得到不同的控制器。所有二阶滑模控制器稳定性的证明由文献 [5] 给出。
Super-twisting滑模控制是一种二阶滑模控制方案,其控制思想是将开关作用的控制量
应用到高阶导数中,这样能有效抑制传统滑模控制中产生的抖振,并能继承传统滑模控制优秀的动态响应和鲁棒性 [6] [7] 。本文中将其引入对转速环的控制中。Super-twisting滑模控制律包含了两个部分:一个不连续的滑模变量函数和一个连续导数的函数,分别如式(3)、(4)所示。
(3)
(4)
其中,增益
、
均为正值;
且滑模变量为
。
其在有限时间内收敛且稳定的充分条件 [8] 是:
(5)
其中,
为
的绝对值的最大值;
为
的最小值;
为
的最大值;
、
为状态变量
的相关函数并由输出量
关于时间
的二阶导数来定义:
(6)
对于开关磁阻电机系统而言,其满足运动方程:
(7)
其中,
为电磁转矩;
为负载转矩;
为转动惯量;
为摩擦系数;
为转子角速度。
对式(7)中的转子角速度进行二次求导,整理后可得:
(8)
根据式(6),则令此时
,
。
由于电机的角速度
,负载转矩
,转动惯量
均为有限值,则一定存在合适的
、
值,使其满足Super-twisting控制器能在有限时间内收敛且稳定的充分条件。
基于以上所阐述的Super-twisting滑模控制理论,转速环滑模控制器可以设计为:
(9)
(10)
其中,
为转子角速度的滑模面函数,
。
3. 改进的直接转矩控制
由SRM的电压平衡方程可知:
(11)
其中,
、
、
和
分别为第
相绕组的电压、电阻、电流和磁链。由于通常情况下,绕组电阻极小,所以忽略绕组电阻的压降,并离散化后可得:
(12)
其中,
为采样周期。将其用矢量三角形的方式描述可得到一个采样周期内磁链的变化值为:
(13)
在扇区
中,当前电压矢量为
,若要增大磁链可选择电压矢量
,若要减小磁链可选择电压矢量为
。则磁链幅值的变化值可表示为:
(14)
(15)
当
时,
对应的夹角
,
对应的夹角
,根据余弦三角函数的特性可知,
的值比
的值小得多,这就会导致在一个采样周期内,磁链幅值的增加与减小存在明显的不同,增加量很少但减少量却很多,使得磁链出现明显的不对称性导致出现转矩抖振。同理,当
时,磁链的增加量明显大于磁链的减小量,而
时增加量和减小量相差不大。所以根据这种特性,本文将每一扇区以
为界近一步细分为三个小扇区,则原来的6个传统扇区可重新划分为18个扇区。
另外,以传统DTC的第一扇区为例,该区域的电压矢量为
,当需要转矩和磁链均增大时,选取电压矢量
,其作用效果应为A相转矩减小,B相转矩增大,C相转矩不变,而实际上由于处在换相区,A相转矩的减小量比B相转矩的增加量大,使得该区域内合成瞬时转矩总体是减小的,出现转矩抖振不能满足转矩控制要求。因此可以增加电压矢量
使B相提前导通,以便在换相时达到期望的转矩。所以,根据对称性本文选择增加六个有效电压矢量,即总共12个有效电压矢量。
综上可以得出相应改进后基于18个扇区的开关矢量表。观察可发现,扇区3、4,扇区6、7,扇区9、10,扇区12、13,扇区15、16和扇区18、1根据控制规则所选择电压矢量相同,因此可将其合并。最终可以得到本文改进后的12扇区电压矢量图,其相应的开关表如表1所示。

Table 1. Switching vector table based on 12 sections
表1. 基于12扇区细分并优化电压矢量后的开关矢量表
4. 系统仿真
最终依据本文理论所设计的基于Super-twisting滑模的SRM直接转矩控制器,主要由SRM本体、功率转换器、扇区判断、开关矢量表、转速控制器等组成,其系统基本原理结构图如图1所示。该控制系统采用了双闭环控制结构,外环为转速环,目标转速和实际转速通过Super-twisting滑模控制器的调节得到系统的参考转矩;内环为转矩、磁链环,将转矩和磁链误差根据直接转矩控制原理,得到控制功率变换器的控制信号以实现对SRM的控制。
为了验证本文所设计的控制系统的有效性,在MATLAB/Simulink中进行仿真实验。仿真中采用了三相12/8开关磁阻电机作为电机本体,功率变换器为不对称半桥电路模型,其系统仿真图如图2、图3所示,各参数设置如下:转动惯量
为0.082 kg∙m2;负载转矩
为1 N∙m;摩擦系数
;磁链给定值为0.25 Wb,磁链滞环为0.01 Wb;转矩滞环为0.1 N∙m;设定的目标转速为500 r/min。
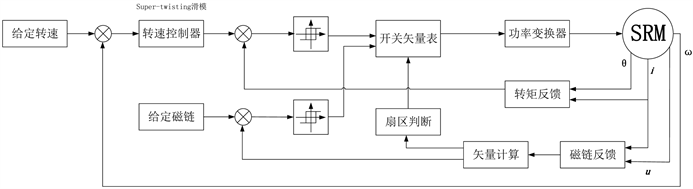
Figure 1. Basic principle structure diagram of SRM system
图1. SRM系统基本原理结构图
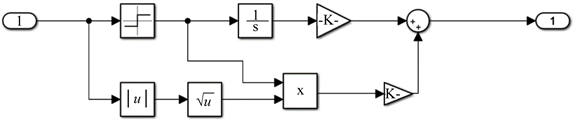
Figure 2. Speed control module based on super-twisting
图2. Super-twisting滑模转速控制模块
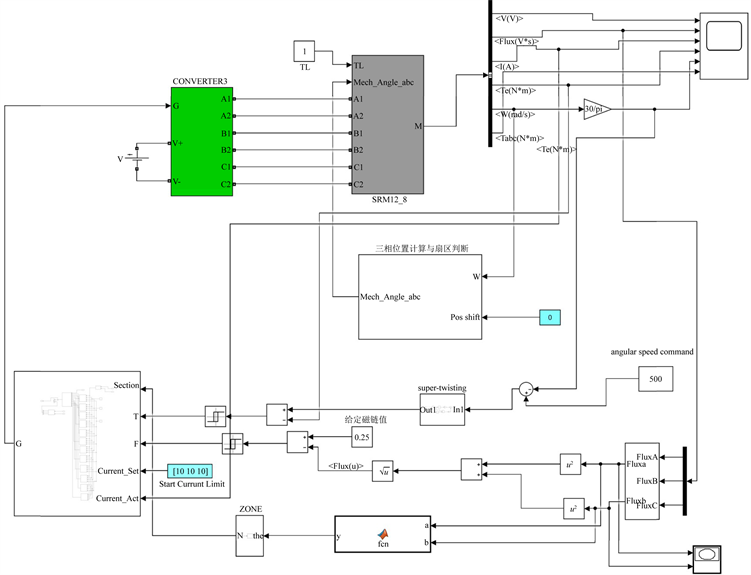
Figure 3. Simulation model of SRM direct torque control system based on Super-twisting sliding mode
图3. 基于Super-twisting滑模的SRM直接转矩控制系统的仿真模型
采用本文所设计的控制器的磁链轨迹、转速及转矩波形分别如图4、图5和图6所示。
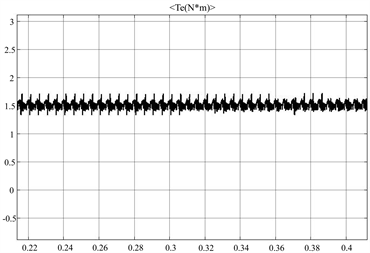 (a) 转矩响应波形
(a) 转矩响应波形 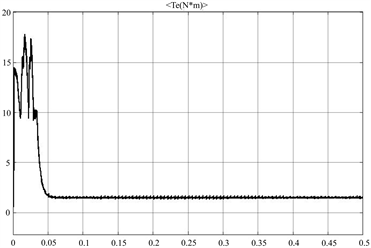 (b) 转矩响应波形局部放大
(b) 转矩响应波形局部放大
Figure 6. Output torque waveform
图6. SRM转矩响应波形
从上述图中可以看出,采用本文所设计的控制系统的SRM转速响应比较快,超调较小,波形较为稳定平滑;磁链近似为一个圆形可知,该控制器对转矩脉动有较好的抑制效果;转矩响应也能较快的到达稳态,稳定后转矩脉动很小仅在1.5 ± 0.2 N∙m左右浮动,基本达到了预想的控制效果。
5. 结论
本文在开关磁阻电机的转速环引入了Super-twisting算法并改进了传统的直接转矩,设计出了一种基于Super-twisting滑模算法的开关磁阻电机新型直接转矩控制器。在MATLAB/Simulink中进行建模仿真分析,其结果表明该方法能在有效地抑制电磁转矩脉动的同时,兼顾系统的转速响应,提高了电机运行的稳定性。