1. 引言
近年来,世界各地的劫机、走私、恐怖袭击等严重安全隐患问题不断出现,旅客与货物安全检查问题逐渐突显出来,使得全球绝大多数国家对机场、车站、港口等口岸的安检作业都更加的重视,在安检技术、通关流程与风险管理上都投入了巨额资金进行相关研究 [1] [2] [3] [4] [5] 。
机场作为贸易往来和供应链运作的重要运输途径之一,机场运行效率及安全水平的高低,不仅体现了一个国家的航空运输业水平,也影响着一个国家的经济竞争力。航空运输在中远距离的人流与物流运输上拥有优势,我国的民用航空运输业更是超前GDP增长速度,在前领跑。根据2017年民航机场生产统计公报 [6] ,我国境内民用航空(颁证)机场共有229个(不含香港、澳门和台湾地区),其中定期航班通航机场228个,定期航班通航城市224个,全年旅客吞吐量超过11亿人次,完成114,786.7万人次,完成货邮吞吐量1617.7万吨,完成飞机起降1024.9万架次。虽然我国航空业发展近40年,航空运输业各项指标都保持着稳步、快速的发展,航空运输在综合交通运输体系中的地位也不断提高,但是仍存在着如机场旅客安检时间过长、航班延误、机场安全水平不高等竞争力问题,有待进一步改进 [7] [8] [9] [10] [11] 。
机场安检时间长短显著影响通关效率与安全,面对效率和安全的双重目标抉择,都是不容忽视的管理问题 [12] [13] [14] [15] [16] 。由此可见,探究如何在资源有限的条件下改进通关安检流程,科学合理提高通关安检系统的保障能力,并使机场安检的服务水平达到最佳,是具有实际意义和应用价值的研究课题 [17] [18] [19] [20] [21] 。
本研究使用仿真软件对机场旅客通关安检流程进行仿真建模,透过一系列实验数据分析,在保证安全水平的前提下,最大化通关效率。通关安检流程的仿真建模可以让管理者直观地看到机场通关安检模拟运行的情况,模拟机场运行过程可能存在的安全隐患问题,并可以通过仿真实验方案的数据分析比较,验证优化策略的可行性和有效性。本文通过对风险门槛值、队长,以及抽查率大小的灵敏度分析,观察旅客安检服务率和通关安全水平的变动趋势,并提出一可行的优化决策变量策略。
2. 基于旅客风险的三安检通道排队安检流程
本文所研究的具有三级检验通道的机场旅客通关安检排队流程如图1所示。旅客通过安检系统(Security-Check System)时,系统会对通关旅客进行风险值评估,随后被分配到与其风险值相符的安检通道进行检查。基于旅客风险的通关安检通道,主要分为严格安检通道(Strict Inspection Channel)、常规安检通道(Normal Inspection Channel)、快速通关安检通道(Fast-Pass Inspection Channel)。严格安检通道相比于其他两个安检通道,安检时间最长,效率最低,但对危险分子的识别率最高。快速通关安检通道相比于其他两个安检通道,安检时间最短,效率最高,但对危险分子的识别率最低。为了追求高安全水平,过多的将通关旅客分配到严格安检通道,会极大的降低旅客通关效率;反之,为了追求高效率通关,而分配过少的旅客人数到严格安检通道,将使得机场安全存在致命的隐患问题。本文通过对仿真模型的优化设计,在可接受的安全水平范围内,使旅客通关安检效率达到最大。

Figure 1. A security-check queuing system with three-level inspection channels
图1. 具有三级检验通道的通关安检排队系统
在图1中,模型参数
表示常规安检通道能够向严格安检通道输送抽查旅客的队列阈值。模型参数
表示快速通关安检通道能够向常规安检通道输送抽查旅客的队列阈值。与严格安检通道、快速通关安检通道不同的是,常规安检通道有一排队上限的队列门阀值M,表示常规安检通道所能容纳的最大旅客队伍长度。当常规安检通道旅客人数超过该队列门阀值M时,进入常规安检通道的旅客将转而进入快速通关安检通道队列中,可以增加通关安检系统的运作效率。当严格安检通道的旅客队列长度小于
时,
表示从常规安检通道进入严格安检通道的旅客到达率。当常规安检通道的旅客队列长度小于
时,
表示从快速通关安检通道进入常规安检通道的旅客到达率。
当严格安检通道的队列长度小于
时,进入严格安检通道的到达率为
;当严格安检通道的队列长度不小于
时,进入严格安检通道的到达率为
。当常规安检通道的队列小于
时,并且严格安检通道的队列小于
时,进入常规安检通道的到达率可表示为
;而只有常规安检通道的队列小于
时,进入常规安检通道的到达率可表示为
。而只有严格安检通道的队列小于
的情况时,进入常规安检通道的到达率表示为
。
当常规安检通道的队列长度大于
并且严格安检通道的队列长度大于
时,进入常规安检通道的到达率可表示为
;当常规安检通道的队列长度小于
时,进入快速通关安检通道的到达率可表示为
。当常规安检通道的队列长度不小于
时,进入快速通关安检通道的到达率可表示为
。
在本研究中,风险门槛值即能够进入相应安检通道的最大值。门槛值是在通关安检系统中用以从风险管理系统区分高、中、低风险旅客进行分流的依据,其赋值范围为0 ≤
≤
≤ 1。假设每一个旅客的风险值相互独立,根据统计资料 [12] ,我们采用通关旅客的风险值服从参数
的截断指数分布,截断指数密度函数如下式:
。
队列阈值(Queue Threshold)表示可允许向低等级安检通道抽调检验旅客的排队长度上限,例如当高一等级安检口的队伍长度达到相应队长时,高等级安检通道不再向低等级安检通道抽查旅客,但本应进入该安检通道的旅客不受影响。抽样概率(Sampling Probability)即高等级安检的队伍长度小于指定值时,低等级安检通道到来旅客被往高一等级安检通道抽查的概率。服务率(Service Rate)即旅客在通关安检中所花费平均等待时间长短。安全水平(Security Level)定义为:
。
在本研究中,具有三级检验通道的排队系统模型参数与系统表现指标,整理如表1所示。
3. Arena仿真建模
本研究通过Arena仿真建模软件建立机场三通道安检模型,Arena建模流程如下:
1) 使用流程图工具,将三通道安检模型的具体流程表示出来;
2) 使用Arena软件相应模块,构建与三通道安检流程图相符的仿真模型;
3) 给Arena仿真模型中各个模块和运行环境设置相对应的参数;
4) 测试模型的功能性与准确性,及时更正仿真模型中的错误;
5) 查看模型的运行结果与报告;
6) 分析实验数据报告。
旅客到达机场后,进入安检系统生成旅客风险值,并对旅客真实风险值进行判断赋值。当该值大于风险阈值时,判定为恐怖分子,并赋值为1,否则赋值为0。接下来,系统根据旅客系统生成的风险值进行旅客分流判断,相应值域内的旅客进入相应的队列进行排队。由于进入常规安检通道较其他两个安检通道的概率会大数倍,因此当进入常规安检通道的排队人数达到一定阈值M时,说明机场当前较为繁忙,後来抵达进入常规安检队列的旅客转而安排进入快速通关安检通道,以降低通关安检的壅塞程度。当严格安检通道当前排队人数小于
时,本应进入常规安检通道的旅客将有概率会进入严格安检通道队列,进行严格安检口检查。当常规安检通道当前队列人数小于
时,本应进入快速通关安检通道的旅客将会有概率进入常规安检通道队列,进行常规安检。通关旅客完成相应安检通道的检查后,结束通关安检流程。
对于每次仿真实验,Arena软件将运行足够长的时间,并且设置足够多的重复试验次数,各模型参数设置将在下一节的计算机访真实验中提供。
4. 实验方案与数据分析
4.1. 实验环境与模型参数设置
在本次研究中,仿真实验环境的操作系统为Windows 10,CPU为Intel Core i5-3230M (2.6 GHz),内存为8 G,仿真建模软件Arena的版本为14.00。本节实验数据来源自Huang等人(2016)对Narita国际机场的实验数据 [13] ,具体实验数据如表2和表3所示:

Table 2. Statistics of departure flights at Narita Airport
表2. Narita机场离港航班人数相关数据

Table 3. Parameter setting of the queuing model for three-level inspection channels
表3. 三级检测信道排队模型的参数设置
由表2和表3,可计算得知平均旅客到达人数为1770.5人,严格安检口的旅客服务率为3.083 (人/分),常规安检口的旅客服务率为18.33 (人/分),快速通关安检口的旅客服务率为9 (人/分)。将相应的数据参数设置到仿真模型中后,开始Arena仿真实验的运行。
本研究中的6个决策变量,主要输入项是在Decide模块中进行参数的设置。决策变量的取值范围如下:快速通关安检门槛值
,间隔为0.005;严格安检门槛值
,间隔为0.03;常规安检通道队列阈值 ,间隔为1;严格安检通道队列阈值
,间隔为1;进入常规安检通道的抽样概率
,间隔为4%;进入严格安检通道的抽样概率
,间隔为4%。
,间隔为1;严格安检通道队列阈值
,间隔为1;进入常规安检通道的抽样概率
,间隔为4%;进入严格安检通道的抽样概率
,间隔为4%。
4.2. 决策参数对系统表现指标的影响
本实验主要目的为研究不同决策变数的灵敏度分析,观察与探讨系统表现的最佳值。我们假设旅客的风险值服从参数为0.0625的截断指数分布。
当进行决策变量
的灵敏度分析实验时,快速通关安检门槛值
的大小服从
,对其余的决策变量进行适当的取值,赋值的结果对
实验趋势研究并无影响。我们假定90%的旅客进入严格安检口,可知相对应的
,旅客平均等待时间W随
的灵敏度变化如图2所示。由数据图2,我们观察到通关旅客的平均等待时间W先减后增,在接近阈值时,平均等待时间W的增大幅度趋于平缓。在快速通关门槛值
时,可得到最小的平均等待时间W。

Figure 2. Data graph of the average waiting time W with respect to the fast-pass threshold
图2. 平均等待时间W相对于快速通关门坎值
的数据图
图3显示机场通关系统安全水平SL随快速通关安检门槛值
的变化曲线图,安全水平SL随快速通关安检门槛值
的增大,无明显变化规律。
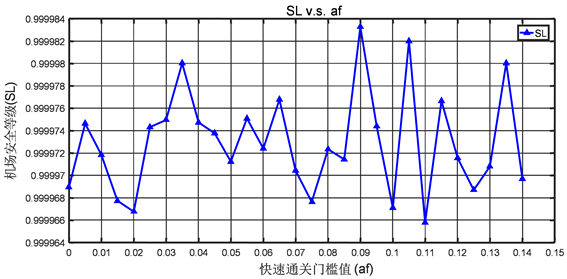
Figure 3. Data graph of the security level SL with respect to the fast-pass threshold
图3. 安全水平SL相对于快速通关门坎值
的数据图
在得知快速通关门槛值
最佳值的条件下,变动输入数值
使得
,可得到通关旅客平均等待时间W随严格安检门槛值
变化的灵敏度分析数据图。由图4可知,旅客平均等待时间随
增大而变小,在一个很小幅度的上升后,平均等待时间W趋于稳定。在严格安检门槛值 处,可得到平均等待时间W的最小值。
处,可得到平均等待时间W的最小值。

Figure 4. Data graph of the average waiting time W with respect to the strict security-check threshold
图4. 平均等待时间W相对于严格安检门槛值
的数据图
通关系统的安全水平SL随严格安检门槛值
变化图如数据图5所示。由图5可知,在严格安检门槛值
的在较小的赋值范围时,系统安全水平SL的表现无明显变化;严格安检门槛值
在较大的赋值范围时,通关系统安全水平SL随着增加
的赋值而变小,最终趋近于一稳定值。
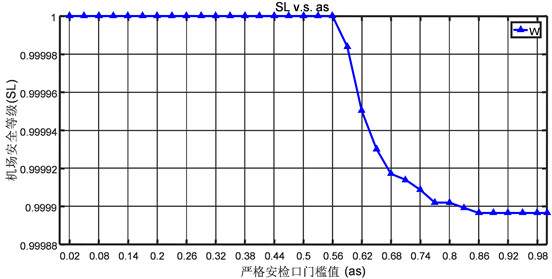
Figure 5. Data graph of the security level SL with respect to the strict security-check threshold
图5. 安全水平SL相对于严格安检门槛值
的数据图
通关旅客平均等待时间W相对于常规安检通道的队列阈值
变化的灵敏度分析如图6所示,我们观察到随着
赋值的增大,旅客平均等待时间W无明显变化规律。
图7表示通关系统安全水平SL相对于常规安检通道的队列阈值
赋值变化的灵敏度分析图,可知通关系统安全水平SL无明显变化规律。
通关旅客平均等待时间W随严格安检通道的队列阈值
变化如图8所示,可知旅客的平均等待时间W随
增大的过程中,先出现一个小幅的下降,后持续变大。虽然后续增大过程中也存在小幅度减少,但总体还是呈明显的上升趋势。在严格安检通道的可抽调旅客队伍长度
时,平均等待时间W达到最小值。

Figure 6. Data graph of the average waiting time W with respect to the queue threshold
of normal inspection channel
图6. 平均等待时间W相对于常规安检通道队列阈值
的数据图

Figure 7. Data graph of the security level SL with respect to the queue threshold
of normal inspection channel
图7. 安全水平SL相对于常规安检通道队列阈值
的数据图

Figure 8. Data graph of the average waiting time W with respect to the queue threshold
of strict inspection channel
图8. 平均等待时间W相对于严格安检通道队列阈值
的数据图
通关系统安全水平SL随严格安检通道队列阈值
变化如图9所示,在变动
赋值的情况下,系统安全水平SL无明显变化趋势。

Figure 9. Data graph of the security level SL with respect to the queue threshold
of strict inspection channel
图9. 安全水平SL相对于严格安检通道队列阈值
的数据图
通关旅客平均等待时间W随进入常规安检通道的抽样概率
变化如图10所示,可知旅客的平均等待时间随
的变化,无明显变化趋势。

Figure 10. Data graph of the average waiting time W with respect to the sampling probability
of entering normal inspection channel
图10. 平均等待时间W相对于进入常规安检通道的抽样概率
的数据图
通关系统安全水平SL随进入常规安检通道的抽样概率
变化如图11所示,可知安全水平SL随
变化,无明显变化趋势。
平均等待时间W随进入严格安检通道的抽样概率
变化图如图12所示,可知平均等待时间W随
的变大,整体呈现下降趋势。在进入严格安检口概率
时,可得到平均等待时间W的最小值。

Figure 11. Data graph of the security level SL with respect to the sampling probability
of entering normal inspection channel
图11. 安全水平SL相对于进入常规安检通道的抽样概率
的数据图

Figure 12. Data graph of the average waiting time W with respect to the sampling probability
of entering strict inspection channel
图12. 平均等待时间W相对于进入严格安检通道的抽样概率
的数据图
通关系统安全水平SL随进入严格安检通道的抽样概率
的数据图表如图13所示,可知安全水平SL随进入严格安检口概率
的变动,无明显影响趋势。
4.3. 实验数据分析总结
从上一小节的实验数据分析图2至图13,可以得知并非六个决策变量都能对系统表现指标W产生明显影响,其中决策变量
、
、
和
对平均等待时间W的影响变化有明显的趋势。例如随着快速通关门槛值
的变大过程中,平均等待时间W在呈现一个小幅度的下降趋势后持续上升,随后上升趋势逐渐减缓,平均等待时间W在
赋值为0.015时,有最小值3.5621。在严格通关门槛值
变化过程中,W随着
的变大,呈快速下降趋势,在
赋值为0.17时,下降趋势迅速停止后,呈缓慢下降趋势,中间有出现一个小幅度上升趋势,后W的值逐渐趋近于一个平稳值。在设置
值为0.62时,平均等待时间W达到最小值3.5620。

Figure 13. Data graph of the security level SL with respect to the sampling probability
of entering strict inspection channel
图13. 安全水平SL相对于进入严格安检通道的抽样概率
的数据图
在严格安检可抽查队列阈值
的变化过程中,平均等待时间W先缓慢下降,后整体呈缓慢上升趋势,在设置叁数
取值为3时,存在平均等待时间W最小值3.3942。进入常规安检通道的抽样概率
在变大过程中,W呈先下降后上升,后持续下降趋势。在
赋值为92%时,存在平均等待时间W最小值3.3192。对于
与
,从变化图中看不出明显的变化趋势,暂定其对W不造成影响。
另一方面,只有一个决策变量造成另一个系统表现指标SL明显的影响趋势。当严格安检口门槛值
取值为0.59时,系统安全水平SL开始出现下降趋势,随着
的变大,SL下降趋势逐渐变缓,最终趋近于一个平稳的值。与严格安检口门槛值
相比较,另外5个决策变量对安全水平SL无明显的影响关系。
5. 优化策略
在本研究中,可以发现模型中有六个决策变量,每个决策变量在数据上又含有多组的变化,如果采用穷举法,对六组决策变量的数值进行排列组合,可能的组合数将超过万种赋值组合,则实际上操作优化策略将会有计算时间与复杂度的局限性。此外,也可以多维的观点将六个决策变量在一个数学优化模型中同时求解,在寻找优化解路径过程中记录系统表现指标最小值的变化,在最终的结果中,将最佳值的那组决策变量的数值选取出来,达到最优的解决方案。
如果不进行决策变量的优化,而只是根据机场通关系统的运行情况,当旅客人数多时,便大幅度增添服务窗口的数目,调用机场后勤保障资源,可能只是在某些时间段内的安检排队人数达到饱和,并非长久持续;当特定拥挤时间段过后,过剩的机场保障资源及过多的闲置通关窗口,都将对机场通关系统的运营绩效带来巨大的成本影响。所以,探讨如何选取通关系统模型变量的优化策略是具有实际意义的。
本文基于数据分析提出优化策略方案,解决通关平均等待时间与系统安全水平的权衡问题。如图14所示,以下是具体的模型变量选取的优化流程。
优化选取模型变量的流程:
1) 选择一个决策变量,结合之前预期跑过的实验数据,提出该决策变数对实验指标的影响,通过与机场实际运行环境的对比,确认决策变量的灵敏度分析范围。
2) 合理选择各组中决策变量数据点的采集间隔。过大的数据点间隔可能影响对优化结果的趋势判断,也可能会在实验流程中错过最佳值的数据点,则将对后续选取决策变量的最佳值产生影响。
3) 实验数据的运行。在完成步骤1与步骤2的基础上,进行仿真模型的输出数据记录,并观察实验结果的灵敏度分析数据图形是否有出现最佳值的趋势。
4) 观察实验指标图行变化,得出一个当前决策变量的最佳数值,同时记录该叁数值与相对应的系统表现指标,并代入下一组决策变量的选取组合中。
5) 选择下一个待定的决策变量,重复进行步骤1到步骤4,直至所有决策变量在本优化流程中运行完毕,则停止运行。

Figure 14. Flow chart of optimizing the selection of model variables
图14. 优化选取模型变量的流程图
我们通过观察决策变量对系统表现指标的灵敏度影响,合理判断是否呈现一个较为明显的变化趋势。如果有造成明显的变化趋势影响,则选取模型决策变量的最佳值,标记在后续的折线图中,与后续流程实验中的系统表现指标进行最佳值的比较。然而,并不是所有的决策变数都能对系统表现指标造成影响,所以只选取能对系统表现指标造成明显变化影响的决策变量赋值。在本节实验中,优化选取模型变量的系统表现结果如图15与图16所示。
由图15可知,在研究优化选取六个决策变量对平均等待时间W的影响过程中,W的最佳值有明显的下降趋势。在实验数据分析图4中,可以看出
能够对W造成明显的影响趋势,但最佳值与图2相近,所以在图形中看不出变化。因为
与 的灵敏度分析图形无明显变化趋势,故不予选取最佳值,则其最佳值采用前一决策变量的最佳值。
的灵敏度分析图形无明显变化趋势,故不予选取最佳值,则其最佳值采用前一决策变量的最佳值。
在图16中,我们观察系统安全水平SL随优化选取六个决策变量的系统表现变化。由于只有
能对其产生影响,所以对于值
的选择并非W所对应的最小值,而是在符合安全水平SL大于99.99%的机场安全指标要求下,且决策变量的赋值需维持安全水平SL整体不变,进而尽量减少平均等待时间W的系统表现数值,由此得到一可行的优化策略。

Figure 15. The optimal value of average waiting time W corresponds to the optimal selection of six decision variables
图15. 平均等待时间W的最佳值对应于六个决策变量的最佳选择

Figure 16. The optimal value of security level SL corresponds to the optimal selection of six decision variables
图16. 安全水平SL的最佳值对应于六个决策变量的最佳选择
6. 总结与展望
本研究对基于风险的三级安全检查信道排队模型进行仿真建模,探讨安检效率和安全水平的管理问题。我们采用Arena仿真软件对机场安检流程进行仿真建模,并通过对多组决策变量进行实验方案比较,优化各个决策变量对系统表现指标的影响。本文以三级安检信道排队流程为仿真模型,通过调整决策变量的数值,例如快速通关门槛值、严格安检门槛值、常规安检通道队列阈值、严格安检通道队列阈值、进入常规安检通道的抽样概率、进入严格安检通道的抽样概率等六个决策变量,进行大量的计算机仿真实验测试,来优化设置基于风险的三级安检信道排队模型的决策变量值。本研究提出的仿真建模优化方案与数据分析,相信能对解决机场三级安检通道排队系统的通关运行效率与安全管理问题,提供有效的实践指导价值。
然而,本研究仍存在一些可继续深研之处,例如在机场安检的实际运行数据分析上,未来可以针对不同地区特性的机场类型采集可信度较高的通关统计数据,进行旅客和货邮大数据分析,较好地预估与设定仿真模型叁数,用以进行相关管理方案设计及其实验。在未来研究工作中,也可考虑模型参数的随机变化,结合概率模型或模糊模型,使研究成果更具有弹性。另外,未来研究也可以探究常规安检通道队列的满员阈值对安检系统的影响分析。在全国通关一体化新背景下,我们应该努力探索安检运作模式与决策分析,在风险管理机制的基础上,改进我国机场通关安检服务,创新落实通关安全与便利并重。
基金项目
本课题得到国家自然科学基金项目(61602117)、福建省科技厅自然科学基金项目(2016J01330)、福建工程学院科研启动基金项目(GY-Z18148)资助。