基于改进型Retinex算法的轴承滚子瑕疵检测系统设计

A Novel Bearing Roller Blemish Detection System Based on Improved Retinex Method

摘要: 基于机器视觉的工件瑕疵检测技术已经成为了重要的发展趋势，然而在实际的检测环境中，光照不均问题对检测结果带来了非常大的影响。因此，光照校正处理成为了机器视觉检测的关键步骤，但是现有的光照校正算法往往存在图像细节丢失的问题，直接影响了检测效果。针对这一问题，提出了一种改进型的Retinex光照校正算法，采用中值滤波代替了高斯环绕函数，从而实现了光照分量的估计，并使用信息熵函数完成了对原图光照均匀程度的判定。同时，基于所提算法搭建了一套轴承滚子瑕疵检测系统，并对所提算法的性能进行验证。实验结果表明，与现有的Retinex系列光照校正算法相比，该算法能够更好地保留工件的图像细节，从而实现更优的检测准确率。

Abstract: The workpiece blemish detection technology based on machine vision has become an important development trend. However, in the actual detection environment, Illumination unevenness has a very large impact on the detection results. Therefore, the illumination correction processing has become a key step in machine vision detection, but the existing illumination correction algorithms often have the problem of image detail loss, which directly affects the detection effect. Aiming at this problem, we proposes an improved Retinex illumination correction algorithm, which uses median filtering instead of Gaussian surround function to realize the estimation of illumination component, and uses the entropy function to complete the illumination uniformity of the original image determination. At the same time, based on the proposed algorithm, a set of bearing roller blemish detection system is built and the performance of the proposed algorithm is verified. The experimental results show that compared with the existing Retinex series illumination correction algorithm, the proposed algorithm can better preserve the image details of the workpiece, thus achieving better detection accuracy.

1. 引言

轴承是现代机械设备中的重要零部件，也是我国重点发展的战略性基础产业之一 [1] [2] [3] 。“十二五”计划明确指出，轴承是加快振兴装备制造业的16个关键领域的核心基石 [4] ，它在多个关键领域有着广泛的应用。作为轴承核心零件之一的轴承滚子，其质量直接决定了轴承的质量。

目前，在轴承滚子质量检测方法中，基于机器视觉的检测方法因为速度快，准确率高等优势，已经成为了轴承滚子质量检测的主流方案 [5] 。基于机器视觉的轴承滚子检测系统通过工业相机来完成待检物表面图像的采集，随后将图像传送到图像处理单元，并完成图像中关键信息的提取和判别，进而实现对轴承表面瑕疵的检测 [6] 。

在实际场景下工作的轴承滚子检测系统中，光照不均匀问题一直是影响其检测性能的难题。由于轴承滚子的材质特性，往往会导致与滚子本身纹理相似的瑕疵难以被检测出来。另外，光照不均现象会对瑕疵的判别带来影响，在轴承滚子图像中，光照不均区域大小、灰度变化的随机性会降低瑕疵判别标准的准确性，从而降低系统的检测准确率。因此，需要在传统的基于机器视觉的轴承滚子瑕疵检测系统中加入光照校正算法，以此来消除光照影响，提高系统检测准确率。

目前应用较多的光照校正方法包括直方图均衡法 [7] 、基于照明–反射模型的同态滤波法 [8] 、基于Retinex原理的光照校正算法 [9] 以及图像边缘增强法 [10] 等。其中，基于Retinex原理的光照校正算法以处理灰度图见长 [11] 。基于Retinex原理的光照校正方法通过使用高斯环绕函数完成了光照分量的估计，而高斯环绕函数的物理意义与均值滤波类似，目标是进行图像平滑，其平滑效果相对于非线性滤波来说更加缓和。因此基于Retinex原理的光照校正算法会将图像中的细节估计为光照分量，从而容易造成光照校正后图像细节的丢失。尤其对于轴承滚子瑕疵检测这种对图像精细度要求很高的应用场景来说，影响更大。

针对当前基于Retinex原理的光照校正算法在轴承瑕疵检测应用场景中的缺陷，本文提出了一种改进型Retinex光照校正算法，采用中值滤波代替了高斯环绕函数，从而实现了光照分量的估计，并使用信息熵函数完成了对原图光照均匀程度的判定。同时，本文设计了一套基于所提算法的轴承滚子表面瑕疵检测系统，并对本文所提算法的性能进行验证。实验结果表明，本文算法能够有效滤除光照并且较好地保留图像细节，同时显著提升轴承滚子瑕疵检测系统的准确率。

2. 轴承滚子瑕疵检测系统

如图1所示，轴承滚子存在五个不同的表面，分别是大/小端面、大/小倒角及侧滚动面。本节将以轴承滚子大端面为例，介绍轴承滚子瑕疵检测系统。

Figure 1. ROI image of each surface of bearing roller

图1. 轴承滚子各表面ROI图像

轴承滚子大端面瑕疵检测系统处理流程如图2所示，包括目标定位与分割、图像预处理、疑似缺陷定位和特征提取与缺陷确认4个主要的步骤。首先，对图像进行二值化处理，进行大端面区域的定位与分割，使用选择后的大端面区域与原图进行掩模操作得到待处理的大端面图像；随后，对定位分割后的大端面图像进行纹理过滤工作，降低纹理对检测的影响；然后，使用阈值分割对图像中出现灰度突变区域分割，定位得到疑似缺陷；最后，提取疑似缺陷特征并进行判断，得到确认缺陷。接下来，将对这4个主要步骤进行介绍。

Figure 2. Machine vision based bearing roller detection system processing flow

图2. 基于机器视觉的轴承滚子检测系统处理流程

2.1. 目标定位与图像分割

本系统使用全局阈值分割方法对大端面区域的进行定位与分割。全局阈值分割分为固定阈值分割与动态阈值分割。固定阈值分割使用固定阈值对图像进行二值化操作，效果精确但是需根据灰度进行人为调整。动态阈值分割针对不同图像得到不同的阈值，效果一般但是参数不需要人为调整。大津法(OTSU) [12] 是具有代表性的动态阈值分割算法，其通过计算前景和背景的灰度方差的最大化，从而得到阈值。

如图3所示，OTSU算法虽然不需要人为调整参数来进行二值化，但是效果与固定阈值相比较差，速度相对较慢。同时，考虑到在实际的检测环境中，整体灰度变化不大，因此本文选择固定阈值进行大端面区域的定位与分割。

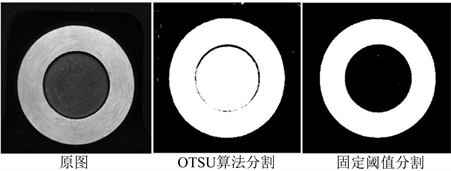
Figure 3. OTSU segmentation and fixed threshold segmentation

图3. OTSU分割与固定阈值分割对比

2.2. 图像预处理

系统中图像预处理步骤的目标是在保留或者不影响图像突变区域特征的前提下尽量滤除图像背景的纹理信息 [13] [14] 。因此，本文选取了各向异性滤波来完成图像的预处理工作，这种滤波方式能够在很好的保留图像边缘的同时，滤除图像纹理。

各向异性滤波通过各向异性扩散方程(P-M方程)完成图像滤波。P-M方程是图像去噪方法中的一个重要模型，其是传统热扩散方程的推广 [15] ，P-M方程定义如下：

$\{\begin{array}{l}\frac{\partial u}{\partial t}=div\left(g\left({\left|\nabla u\right|}^2,c\right)\cdot \nabla u\right)\hfill \\ u_0=u\left(x,y,0\right)\hfill \end{array}$ (1)

式中， $g\left({\left|\nabla u\right|}^2,c\right)$ 代表扩散系数，它根据图像的梯度来变化。 $\nabla u$ 代表图像梯度， $div$ 是散度算子， $u_0$ 是原始图像， $u\left(x,y,0\right)$ 是 $t$ 时刻 $u_0$ 的扩散图像。

2.3. 疑似缺陷定位

疑似缺陷是图像中的灰度突变区域。本文使用阈值分割方法来进行疑似缺陷的定位。上文中提到，鉴于固定阈值分割能够满足场景要求，因此采用固定阈值分割方法完成疑似缺陷定位。

在实际场景中，可将疑似缺陷分为疑似亮缺陷和疑似暗缺陷两类，具体定义如下：

$d\left(x,y\right)=\{\begin{array}{l}{\text{flaw}}_{\text{light}}\left(x,y\right),f\left(x,y\right)\ge T_l\hfill \\ {\text{flaw}}_{\text{dark}}\left(x,y\right),f\left(x,y\right)\le T_d\hfill \\ 0\le T_d<T_l\le 255\hfill \end{array}$ (2)

式中， $d\left(x,y\right)$ 是已定位疑似缺陷中的像素， ${\text{flaw}}_{\text{light}}\left(x,y\right)$ 是疑似亮缺陷中像素， ${\text{flaw}}_{\text{dark}}\left(x,y\right)$ 是疑似暗缺陷中像素， $f\left(x,y\right)$ 是大端面中像素灰度值， $T_l$ ， $T_d$ 是进行疑似亮缺陷、疑似暗缺陷分割的阈值。本系统将大端面图像中灰度值高于 $T_l$ 的像素点定义为疑似亮缺陷 ${\text{flaw}}_{\text{light}}\left(x,y\right)$ ，将大端面图像中灰度值低于 $T_d$ 的像素点定义为疑似暗缺陷 ${\text{flaw}}_{\text{dark}}\left(x,y\right)$ 。

2.4. 缺陷确认

轴承滚子大端面中存在的主要缺陷如图4所示，主要有锈斑、划伤、欠磨等。锈斑具有灰度深且面积不定的特性；划伤具有灰度深、区域狭长、具有一定宽度的特性；欠磨具有其面积与非欠磨区域面积相差巨大的特性。针对各种缺陷特性，本文提取了灰度特征中的灰度均值特征、形状特征中的面积特征以及纹理特征中的对比度特征来描述疑似缺陷。

Figure 4. Defect type

图4. 缺陷类型

面积特征通过统计疑似区域中像素数得出 [16] ；纹理特征中的对比度特征通过灰度共生矩阵GLCM (Gray-level co-occurrence matrix) [17] 计算得出，GLCM描述了存在于不同方向和距离的像素对的出现频率。根据GLCM可得对比度的定义如下：

$\text{Contrast}={\displaystyle \underset{i=1}{\overset{K}{\sum }}{\displaystyle \underset{j=1}{\overset{K}{\sum }}{\left(i-j\right)}^2{p}_{ij}}}$ (3)

式中， $K$ 是图像中的最大灰度级， $i$ , $j$ 分别代表对应的像素的灰度， $p_{ij}$ 是在角度 $\theta$ 方向上相距 $s$ 的两个像素灰度为 $i$ , $j$ 的情况的出现频率。

3. 改进型Retinex光照校正算法

Retinex光照校正算法以处理灰度图见长，同时也能够保证较快的处理速度。然而，现有的Retinex光照校正算法存在严重的细节丢失问题。因此，本文提出了一种改进型的Retinex光照校正算法。

3.1. Retinex理论

Retinex理论认为图像 $I\left(x,y\right)$ 由光照分量 $L\left(x,y\right)$ 和反射分量 $R\left(x,y\right)$ 组成，即：

$I\left(x,y\right)=R\left(x,y\right)\times L\left(x,y\right)$ (4)

根据Retinex理论，反射分量 $R\left(x,y\right)$ 应该尽可能保留，而光照分量 $L\left(x,y\right)$ 应该尽可能去除。

因为光照分量 $L\left(x,y\right)$ 与反射分量 $R\left(x,y\right)$ 的不可分性，因此需要将图像转换为对数域，得到可分的光照分量和反射分量。将图像转换为对数域之后，得到：

$\log I\left(x,y\right)=\log R\left(x,y\right)+\log L\left(x,y\right)$ (5)

接下来使用平滑滤波函数对原图 $I\left(x,y\right)$ 平滑操作，进行光照分量 $L\left(x,y\right)$ 的估计。至此，即可分离出反射分量 $R\left(x,y\right)$ ，得到光照校正后的图像。具体的流程如图5所示：

Figure 5. Basic process of Retinex principle

图5. Retinex原理基本流程

Retinex原理中核心步骤是对光照分量 $L\left(x,y\right)$ 的估计。根据估计方式的不同，基于Retinex原理的光照校正算法可分为单尺度Retinex光照校正算法 [18] 、多尺度Retinex光照校正算法 [19] 等。

3.2. 基于Retinex的优化算法

3.2.1. 单尺度Retinex光照校正算法

在单尺度Retinex光照校正算法SSR (Single-scale Retinex)中，使用高斯环绕函数来进行光照分量 $L\left(x,y\right)$ 的估计。高斯环绕函数定义如下：

$f\left(x,y\right)=\lambda {\text{e}}^{-\left(x^2+y^2\right)/2{\sigma }^2}$ (6)

式中， $\sigma$ 为尺度参数； $$ 需满足以下条件：

${\displaystyle \iint F\left(x,y\right)\text{d}x\text{d}y=1}$ (7)

SSR光照校正算法使用单一尺度 $\sigma$ 进行光照分量的校正。由于参数固定，难以处理复杂图像的光照校正问题，并且应用场景单一。为了解决这个问题，Jobson [19] 等人提出了多尺度Retinex光照校正算法MSR (Multi-scale Retinex)。

3.2.2. 多尺度Retinex光照校正算法

MSR算法通过采用多个不同尺度的高斯环绕函数进行光照分量的估计，然后将这些处理结果进行叠加，以期获得更好的光照校正效果，MSR算法定义如下：

$R\left(x,y\right)={\displaystyle \underset{i=1}{\overset{N}{\sum }}{w}_k\left\{\log I_i\left(x,y\right)-\log \left[I_i\left(x,y\right)*f_k\left(x,y\right)\right]\right\}}$ (8)

式中， $w_k$ 为权重， $i$ 是高斯环绕函数的索引。高斯环绕函数定义如下：

$f_k\left(x,y\right)={\lambda }_k{\text{e}}^{-\left(x^2+y^2\right)/2{\sigma }_k^2}$ (9)

式中， ${\sigma }_k$ 为 $f_k\left(x,y\right)$ 的标准差， ${\lambda }_k$ 通过SSR算法中的计算方式得到。

3.3. Retinex光照校正算法的改进

MSR算法增加了SSR算法对不同场景的适应能力。但是MSR算法与SSR算法的光照分量估计方法的基本原理相同，它们使用高斯环绕函数对图像进行处理，从而得到光照分量。高斯环绕函数与线性滤波算法的物理意义类似，都是进行图像平滑操作。线性滤波算法相对于非线性滤波算法具有更加缓和的图像平滑效果，因此高斯环绕函数对图像进行光照分量的估计时，会获得更多的原始图像细节。从而在进行光照分量与反射分量分离时，减少了反射分量中的细节，而反射分量恰恰需要进行图像细节的保留。因此使用高斯环绕函数这种类似线性滤波方式进行光照分量估计时，会造成图像光照校正后的细节丢失。

针对这种问题，本文采用中值滤波进行图像光照分量的估计，中值滤波作为一种效果明显的非线性滤波方法，能够有效增加对图像的平滑效果，以此缓和图像的细节丢失问题。同时使用图像的信息熵函数(Entropy)作为光照分量的均匀性的检测标准，以此来判定原图是否光照均匀，进一步避免在实际项目中不必要的计算，减少计算量。

3.3.1. 中值滤波原理

中值滤波的原理是将图像中某像素点八邻域或四邻域的像素按灰度值进行排序，然后选择排序中间位置的像素灰度值代替该像素点灰度值 [20] 。中值滤波的定义如下：存在一组数 $x_1,x_2,\cdots ,x_n$ ，把这n个数进行从大到小的顺序排列如下：

$x_{i1}\le x_{i2}\le \cdots \le x_{in}$ (10)

式中， $i$ 表示第 $i$ 组数，在图像中即为第 $i$ 个像素。将上式表示将第 $i$ 个像素周围相邻的n个像素进行从大到小排序得到：

$y=Med\left\{x_{i1},x_{i2},\cdots ,x_{in}\right\}$ (11)

式中， $y$ 称为序列的中值。

3.3.2. 图像光照均匀性检测

信息熵是表现图像的信息量的多少和像素灰度值的变化剧烈大小的客观评价标准，因此作者使用信息熵函数描述图像的精细程度和均匀性 [21] 。

信息熵函数的定义如下：

$E=-{\displaystyle \underset{i=0}{\overset{L-1}{\sum }}{P}_e\left(i\right)lb\left[P_e\left(i\right)\right]}$ (12)

式中， $P_e\left(i\right)$ 用于描述图像中灰度值为 $i$ 的像素个数； $L$ 用于描述图像中存在的灰度级个数。

3.3.3. 算法处理流程

基于中值滤波与Retinex原理的光照校正算法工作流程如图6所示，具体包括：

Figure 6. Algorithm processing flow

图6. 算法处理流程

第一步：首先将原图 $I\left(x,y\right)$ 转换到对数域；

第二步：使用中值滤波进行图像平滑操作，得到光照分量 $L\left(x,y\right)$ 如下：

$L\left(x,y\right)=I\left(x,y\right)*Med\left(x,y\right)$ (13)

式中，*代表图像卷积运算；

第三步：对光照分量 $L\left(x,y\right)$ 进行信息熵计算，判断 $L\left(x,y\right)$ 是否均匀。如果 $L\left(x,y\right)$ 均匀，则原图 $L\left(x,y\right)$ 光照均匀，结束本算法。若光照不均匀继续执行下一步；

第四步：使用原图对光照分量进行逐像素相减，得到 $\log R\left(x,y\right)$ ，具体如下：

$\log R\left(x,y\right)=\log I\left(x,y\right)-\log L\left(x,y\right)$ (14)

第五步：将对数域中的图像通过逐像素指数操作，得到时域中的图像 $R\left(x,y\right)$ ；

第六步：对恢复到时域后的图像进行灰度值拉伸。

4. 仿真与结果分析

本小节使用主观评价和客观评价两种方式对比MSR算法和本文提出的算法，从而验证本文提出的算法的功能性。同时将本文算法加入到轴承检测系统中，对比加入光照校正前后系统的准确率和时间的变化。

4.1. 实验环境搭建

4.1.1. 样本的选取

为了提升系统仿真结果的客观性，本文从轴承工厂中随机选取了约1000枚轴承滚子进行算法及系统性能的测试。同时，为了验证算法的普适性，本文选取了四种不同类型的光照不均图像，这四张光照不均图像基本涵盖了在实际生产线中存在的光照不均类型，具体如图7(a)、图7(d)、图7(g)、图7(j)所示，分别是存在单块光照不均区域、存在多块分散的光照不均区域、存在多块分散光照不均区域的同时存在灰度值与背景差异较小区域以及存在多块分散光照不均区域的同时存在灰度值与背景差异较大区域。

Figure 7. Comparison of MSR algorithm and processing results of this algorithm

图7. MSR算法与本文算法的处理结果对比

4.1.2. 仿真软硬件环境搭建

本仿真在CPU为Intel (R) Core (TM) i3-3220型号的PC机中完成。算法使用Windows7操作系统配合Halcon12机器视觉软件完成运行。

4.2. 算法仿真结果及分析

4.2.1 . 算法对比实验主观结果分析

光照分量在图像中的特征与人类的主观感受接近，因此在进行光照校正结果判断的时候，认为主观感受应作为实验结果的考量条件之一。主观评价将从图像细节变化情况入手进行分析。

图7第(1)行图像，使用MSR算法进行光照校正后，整体均匀度提升，但是丢失了部分原图应有的细节。而使用基于中值滤波与Retinex原理的校正算法处理后，均匀度同样提升，同时基本不丢失原图细节。具体细节丢失情况如方框内图像所示。

图7第(2)行图像，使用MSR算法进行光照校正后，图像均匀度提升效果明显，但同时出现细节丢失问题。而使用基于中值滤波与Retinex原理的校正方法处理后，图像均匀度提升的同时，基本没有丢失细节，具体对比如方框内图像所示。

图7第(3)行图像，存在疑似缺陷，如方框中图像所示。使用MSR算法处理后方框中疑似缺陷出现细节丢失问题，同时疑似缺陷的灰度与其周边区域的灰度的差别减少。而基于中值滤波与Retinex原理的校正方法的细节丢失问题基本没有出现，并且方框内疑似缺陷灰度与其周边区域的灰度的差别没有出现明显的减少问题。

图7第(4)行图像，存在疑似缺陷，如方框中图像所示。使用MSR算法处理后同样出现细节丢失，且疑似缺陷的灰度与其周边区域的灰度的对比度也相对原图降低。使用基于中值滤波与Retinex原理的校正方法处理后，光照均匀性提升明显，且方框内疑似缺陷的灰度与其周边区域的灰度变化差别变化较少。

同时从不同算法对不同图像的整体处理结果可得，由于本文的算法使用了单一尺度的中值滤波对图像进行光照分量的估计，因此本文提出的算法与SSR算法一样能够将图像整体灰度变化稳定在一个很小的范围，更加便于光照校正后的图像处理。而MSR使用了多个尺度的高斯环绕函数对图像进行光照分量的估计，因此使用MSR算法处理后，不同图像的整体灰度差异相对较大，这种结果会对光照校正后的图像处理造成一定的影响。

4.2.2 . 算法对比实验客观结果分析

本文选择信息熵函数(Entropy)和图像灰度均值(Mean)作为图像客观评价标准。信息熵函数作为图像精细度、均匀性的指标，信息熵越大，图像细节越多，信息熵越小，图像细节越少。图像灰度均值用来描述不同图像间灰度的变化情况，不同图像间灰度均值变化越大，对图像后续处理的影响越大；灰度均值变化越小，对图像后续处理的影响越小。

具体的客观评价结果如表1所示。在使用MSR算法进行光照校正后，信息熵降低，说明图像经过处理后完成了对部分光照细节的滤除，同时，灰度均值变化相对原图来说更小，但是同样存在较大的差异。

Table 1. Comparison of objective evaluation results

表1. 客观评价结果对比

而使用本文提出的方法对原图进行光照校正后，信息熵降低的同时，保证了灰度均值基本保持在同一个层次上，说明图像光照不均匀细节去除较好，同时与MSR算法相比，信息熵提升较大，保留了图像本身更多细节，并且对图像后续处理的影响相对MSR算法来说更小。

4.2.3 . 算法处理时间对比

如图8所示，MSR算法与本文提出的算法处理时间均基本维持在100 ms左右。根据算法结果的主客观分析可知，本文提出的算法能够较好的完成图像细节的保留，同时能够保证算法处理时间与MSR基本一致。说明本文提出的算法在不额外占用系统处理时间的前提下，获得了更好的处理效果，极大的提升了系统的处理效率。

Figure 8. Comparison of processing time between MSR algorithm and the algorithm of this paper

图8. MSR算法与本文算法的处理时间对比

4.3. 系统仿真结果及分析

光照校正模块完成了图像光照的校正之后，需要对图像中可能存在的缺陷进行进一步的提取与分析，从而得出滚子合格与否的结果。

实验随机选择了约1000枚轴承滚子进行检测，分别使用人工检测、未加入光照校正模块检测系统、加入本文光照校正算法检测系统三种方式进行检测，并对检测时间进行统计。

由表2可知，在进行轴承缺陷检测时，人工检测的结果出现偏差很小，出现了10个漏检；未加入光照校正的检测系统出现了18个误检，与人工检测相比偏差很大；而加入光照校正之后，检测系统仅出现了2个误检，大幅降低了误检个数，有效的提升了系统的检测准确率。加入光照校正检测系统的检测准确率在提升的同时，也与人工检测相比大幅降低检测时间，极大的提高检测效率。

5. 结论

对精细度要求较高图像进行光照校正是一种较为常见的需求。本文在这方面进行了尝试，通过改进MSR算法中的光照分量的估计方式来进一步提升光照校正算法对图像细节的保留程度。该算法通过使用中值滤波来进行光照分量的估计，同时对光照分量的信息熵Entropy进行判断，从而对原图进行光照均匀度的判别，进一步的减少光照校正算法的处理时间。

Table 2. System detection and manual detection

表2. 系统检测与人工检测对比

同时，本文设计了一种基于机器视觉的轴承滚子缺陷检测系统，并将本文提出的算法应用到系统中，提升了系统的检测准确率，同时也与人工检测相比大幅降低检测时间，极大的提高检测效率。