1. 引言
在过去几十年,高维回归在基因学、金融、图像处理、气候科学、传感器网络等领域有着广泛应用。经典的高维线性回归模型假设预测变量的维数n总是大于样本的数量m,尽管有效的预测变量的维数s总是远小于n的。零模正则化在统计、机器学习、信号与图像处理、稀疏模型选择和误差修正、金融工程及量子计算等领域中有着广泛的应用。这种非凸正则为稀疏恢复提供了一种有效的方法。然而,在高维的问题中却很难分析。
2. 零模正则复合优化问题
2.1. 零模正则问题
设
是赋予了内积
及诱导范数
的有限维向量空间。考虑零模正则规划:
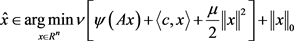 (1)
(1)
其中
是正则项系数,
为连续可微强凸函数,
为设计矩阵,
为已知向量,
为任意小的常数,
为系数向量,
为向量
中非零元个数。该模型将为以后的逻辑回归研究作铺垫 [1] [2]。记 ,则函数
是全局Lipschitz连续的,记其Lipschitz常数为
[3]。由于零模函数的不连续性和非凸性质,(1)这种问题通常是NP难的,难以求得其全局最优解。一个常用的处理方法是使用凸松弛技术,这种方法通过解一个或一系列在数值上易于处理的凸优化问题来产生一个理想的局部最优解或至少一个可行解。
,则函数
是全局Lipschitz连续的,记其Lipschitz常数为
[3]。由于零模函数的不连续性和非凸性质,(1)这种问题通常是NP难的,难以求得其全局最优解。一个常用的处理方法是使用凸松弛技术,这种方法通过解一个或一系列在数值上易于处理的凸优化问题来产生一个理想的局部最优解或至少一个可行解。
2.2. 零模问题的等价Lipschitz替代
本文将从问题(1)的等价MPEC问题和这个MPEC问题的全局精确罚问题中得到解估计
,并证明
可以通过求解一个精确罚问题得到。令
代表闭适当凸函数
且
的函数
族,其中
满足下面的条件:
,
, 且这样的
是唯一的。
且这样的
是唯一的。
令
为
中的最小元素,由下面引理(参考文献 [4] 引理5)可知这样的
存在:
引理1:令
,存在
使得
,且对任意给定的
和
,最优值
满足:
下面将说明对任意
,问题(1)可以重写为一个等价MPEC问题。不难验证:对任意给定的
和
,
(2)
因此问题(1)等价于:
(3)
假设问题(1)有非空全局最优解集且最优值为
,由文献 [4] 可得如下引理:
引理2:令
,零模正则问题(1)等价于问题(3)。当
是问题(1)的全局最优解时,
是问题(3)的全局最优解且最优值等于
;相反的,若
是问题(3)的全局最优解,那么
是问题(1)的全局最优解且
。
问题(3)的可行集中包含着如下互补约束:
,
且
。这说明零模正则化问题也是一个带有互补约束的数学规划问题(MPEC),但是MPEC在优化中也是一类很难的问题。虽然(3)的目标函数比原问题(1)简单,但却含有非凸互补约束
,这将比非凸目标函数更难处理。为解决这个非凸约束,考虑问题(3)的罚问题:
(4)
其中
是罚参数。下面的定理将说明问题(4)是问题(3)的全局精确罚,即它们有相同的全局最优解集 [4]。
定理1:令
。对所有
,有
。这里
是与
相关的问题(4)的全局最优解集,
是问题(3)的全局最优解集。
由定理1,零模正则问题(1)的解估计量
可在
时,由求解问题(4)得到,即:
,其中
。 (5)
由于
,函数
在
上是Lipschitzian连续的,所以问题(5)在其可行集
上也是Lipschitzian连续的。对任意
,定义相应的函数
:若
,
;若
,
。问题(5)可以重新写为更简便的形式:
。
由共轭函数的定义和以上讨论,可以得到:
,其中
(6)
这意味着下面的函数是
的等价DC替代:
。
3. 多阶段凸松弛法
从上一节可知,求解零模正则化问题的解估计
,对于
且
时,可由求解罚问题(5)得到。当给定
时,阀值
是容易计算得到的。对一个给定的
,虽然罚问题(5)是非凸的,但是这种结构使得它比零模正则化问题更好解决。特别的,当变量
选定时,问题(5)退化为关于
的凸的极小化问题;当变量
选定时,问题(5)退化为关于
的凸的极小化问题,后面将看到这样的问题是有闭式解的。基于此,本文将通过使用多阶段凸松弛法交替求解问题(5)来得到解估计
[5]。
算法1. (GEP-MSCRA求解
)
Step 0:取
,
和初始点
。置
。
Step 1:令
并计算下面的极小化问题:
。 (7)
若
,由
的取值选取参数 并使
。
并使
。
Step 2:计算下面的极小化问题:
。 (8)
Step 3:置
,返回(S. 1)步。
注1:由函数
的定义,
是(8)的最优解当且仅当
,
。由于
是R上的凸函数,次微分
是容易求得的。因此,多阶段凸松弛法每次迭代的计算难度都在于解决问题(7),即一个加权
范数正则化问题 [6] [7] [8]。这是一类凸优化问题,它可以通过标准的凸优化方法求解,比如:增广拉格朗日法,内点法 [9],IRLS-LARS [10],路径跟踪法,迭代加权最小二乘法等。对于多阶段凸松弛法,下面的命题(参考文献 [4] 注释3.1)说明一旦满足互补条件,迭代点
就是原问题(1)的局部最优解。
命题1:对任意的
,
为算法1生成的迭代点。若
,则
是原问题(1)的局部最优解;且当
时,对于
,
是问题(5)的局部最优解。
4. 理论分析
这节内容主要关注在限制强凸条件下,针对
,多阶段凸松弛法的收敛性分析。假设
是真实解,本文将建立迭代点
到真实解
的误差界,并证明误差数列随着
的增长是严格下降的。记
,
,则
。对
和整数
,定义集合:
。
若矩阵A满足:对任意
,
成立,则称矩阵A在集合
上满足
,其中
。假设噪音向量
中的元素是独立次高斯的,则下面的假设成立:
假设1:假设
是独立次高斯分布的,即:存在
,使得对所有
和
,
。
为给出每一迭代步
到真实解
的误差界,需要将参考文献 [4] 引理7,8拓展为下面一些引理:
引理3:对于
,记
,
。若存在一个指标集
,使得
,则当
时,下式成立:
。
证明:对于问题(7),
和
分别代表最优解和可行解,则有:
由于
,所以:
(9)
由于
在
上是强凸的,即:
,且
,所以,
(10)
再由引理条件
,即可得到不等式。证毕。
引理4:对于
,若存在一个指标集
,使得
,且矩阵A在集合
上满足常数
的限制强凸条件(RSC),则当
时,下式成立:
。
证明:由引理3可知,
,再由(9)式得到:
(11)
因此,结论得证。证毕。
下面给出迭代点到真实解的误差界。由参考文献 [4] 定理4.1可得:
定理2:令
,假设矩阵A在集合
上满足常数
的限制强凸条件(RSC),且
。若
,则
定理2虽然给出了多阶段凸松弛法产生的迭代点的误差界,但是依然不清楚当前迭代点
的误差界是否优于先前迭代点
,即误差界数列是否下降。下面的定理3(参考文献 [4] 定理4.2)对所有
,通过
和
界定
解决了这一问题,其中
,
,
且
。首先对
,通过
和
,给出
的上界(参考文献 [4] 引理9)。
引理5:对每一个 ,令
为上面定义的指标集,则有:
。
,令
为上面定义的指标集,则有:
。
定理3:假设矩阵A在集合
上满足常数
的限制强凸条件(RSC),若参数
和
的选取与定理2一样,则对所有的
:
。
由定理3可知:
的误差界与
的误差界紧密相关,且若前者充分小,则后者也将很小。然而,若
选择恰当,即使
的误差界很大,
的误差界也将很小。定理还说明误差数列随着
增大而递减,递减到
,称之为统计误差。统计误差包含两部分:第一部分是由噪声引起的,第二部分是由
,
和
的选择产生的。
5. 结论
本文从零模函数的变分刻画入手,将这类带有组合性质的优化问题等价转化为具有拟双线性结构且全局Lipshitz连续的优化模型,以此设计了求解零模正则化复合优化问题的多阶段凸松弛方法,并对该方法进行了收敛性分析。在理论方面,本文证实了将文献 [4] 的理论结果即:在比限制等距性质(RIP)更弱的限制强凸条件下,定量刻画了多阶段凸松弛法每阶段最优解的误差界,且每阶段最优解的误差界递减拓展到复合模型的有效性,将为以后研究逻辑回归奠定理论基础。以后将证明当阶段数达到一定条件后,误差界保持不变且精确识别真实解的支撑集。
致谢
感谢贲树军师兄给予的帮助。
参考文献