人工智能在水文预报中的应用研究

Hydrological Forecasting Using Artificial Intelligence Techniques

摘要: 全面论述了数据驱动水文模型中人工智能的关键技术及其适应范围，分析了机器学习在水文预报中遇到的技术瓶颈。采用Gamma Test对数据驱动模型进行输入优选，降低了模型的白噪声误差影响；提出了长短期记忆神经网络与批量学习、正则化、筛选神经元技术相结合的深度学习网络，以解决变化环境下降雨–洪水过程统计特征的非线性、随机性和时变性问题。长江上游向家坝~三峡水库区间流域的应用结果表明：在不考虑未来降雨预报的前提下，仅以前期和现时已知的降雨–洪水资料为模型输入，长短期记忆动态神经网络结合三种深度学习辅助算法，防止模型的过参数化和过拟合，有效提高了三峡水库入库洪水的预报精度，1~3 d预报精度均达到了甲等水平。

Abstract: The key techniques and bottlenecks of artificial intelligences in data-driven hydrological model were reviewed thoroughly. Gamma test method was used to optimize the input combination of data-driven model to reduce the white noisy error. The machine learning techniques, such as batch-size learning, regularization and drop out neuron were incorporated into a long-short-term memory (LSTM) deep learning neural network to simulate nonlinear, stochastic and non-static processes in hydrological forecast under changing environment. The application results in study area between Xiangjiaba and Three Gorges Reservoir inter-basin indicate that the forecasting accuracy from one to three days lead-time reaches A-grade (reliability ≥ 85%) and is improved effectively by integrating LSTM neural network and three deep learning auxiliary algorithms in the interests of conquering model over parameterization and overfitting bottlenecks.

1. 引言

水文预报是防汛抗旱决策、水资源合理利用、生态环境保护以及水利水电工程运行管理的重要依据。水文预报通常根据前期和现时已知的水文气象资料，以流域水文模型为工具对未来一定时间内水文要素的状态做出定量的预测。近几十年来，随着流域产汇流理论研究的深入、计算机技术的迅速发展和预报实践经验的增加，水文预报技术在理论和实践上都取得了长足发展 [1] [2] 。人工神经网络和数据挖掘方法均属于人工智能技术的范畴，因其处理非线性和不确定性的强大能力，在水文预报领域取得了丰硕的研究成果 [3] 。其中人工神经网络根据网络架构是否有回馈项(又称为递归项、循环项)可划分为静态神经网络和动态神经网络，前者的网络架构没有回馈项，对资料结构的长期映射关系具有较好的解析效果，而后者的网络架构具有回馈项，对资料结构的短期映射关系具有较好的解析效果；其次根据隐含层的数目，又可分为浅层神经网络(隐含层仅为1层)和深度神经网络(隐含层数 ≥ 2层)。在水文预报领域应用较广的静态类神经网络包括反向传播神经网络、径向基神经网络、自组织映射网络、时滞神经网络、适应性网络模糊推论系统等 [4] [5] [6] ；应用较广的动态类神经网络包括Elman回馈式神经网络、即时回馈式神经网络、非线性自回归外因输入模式等 [7] [8] 。

动态神经网络具有良好的短期记忆能力，其网络训练算法为误差向后传播演算法，训练过程中易表现出以下两种现象：1) 当梯度值大于1.0时，误差就会随着反向学习时间步长的增加而呈指数增长，那么网络的参数更新会引起损失函数非常大的震荡，即梯度爆炸现象；2) 当梯度值小于1.0时(如接近0)，误差就会随着反向学习时间步长的增加而呈指数降低，也就是后面时间节点对于前面时间节点的感知力下降，使得网络权重更新缓慢，导致梯度学习过程停滞不前，陷入局部最优解，这就是梯度消失现象。基于误差向后传播演算法的回馈式神经网络，随着反向学习时间步长的增加，一旦出现梯度爆炸或消失现象，就会导致动态神经网络长期记忆能力的丧失 [9] 。

对于那些夹杂大量噪声的数据，为了提高数据的信噪比，在使用之前，常常需要进行降噪处理。数据挖掘方法作为人工智能技术的重要分支，与人工神经网络之间有着紧密联系。数据挖掘方法，如小波转换、主成分分析法、聚类算法、Gamma Test等，可从时空层面上提高数据资料的精确性、完整性、一致性、时效性和可靠性等 [10] [11] [12] ，从而可有效提高数据驱动模型的精度和稳健性。

由于变化环境导致水文过程统计特征的非线性、随机性和时变性现象愈发显著。传统静态和动态神经网络，无法有效地模拟变化环境下的降雨–径流关系。因此，如何适应变化环境及实现智慧预报，是水文科学研究领域极具挑战性的技术难题之一。本文重点研究探讨以下三个关键技术问题：1) 如何解决传统静态和动态神经网络在深度学习过程中引发的梯度爆炸现象和梯度消失问题？2) 如何应用具有长短期记忆能力、回馈连接与外部输入的深度神经网络，使神经元和隐藏层中自动选择记忆或遗忘前期的降雨–径流时空关系，模拟水文过程统计特征的非线性、随机性和时变性；3) 对比分析传统静态、动态神经网络与新颖深度神经网络对变化环境下降雨–径流的时空映射进行推估预测的能力。

2. 研究内容及关键技术

为充分展示数据挖掘方法和机器学习模型对降雨~径流的时空映射进行动态推估预测能力，本研究内容及采用的相关方法详述如下：1) 采用Gamma Test数据挖掘方法，探讨集水区气象水文数据在时空上的交互关系，并筛选出数据驱动模型的输入因子；2) 接着对比分析三种神经网络数据驱动模型，即静态神经网络(BPNN)，动态神经网络(NARX)和长短期记忆神经网络(LSTM)，其中具有长短期记忆能力、回馈连接与外部输入的LSTM神经网络可在神经元和隐藏层中自动选择记忆或遗忘前期的降雨-径流时空关系，以实现对降雨-径流的时空映射进行动态推估预测；3) 最后结合三类深度学习的辅助算法，来处理LSTM长短期记忆神经网络模型的参数和结构不确定性，防止模型的过参数化和过拟合，并对模型精度进行评估。

2.1. 数据输入选择

Gamma Test由Stefánsson等人于1997年提出，它是一个独立于模型的数据分析方法，属于资料导向的统计分析方法，可估计资料中包含噪声的程度，具有良好的实用性 [11] 。Gamma Test具有以下三个功能：1) 确定训练出最优数据驱动模型的最小数据集；2) 时间上：依据洪水传播时间，确定输入变量的最优时滞；3) 空间上：确定输入变量最优组合。由于执行一次Gamma test耗时短，因此可将众多可能输入因子同时放入，评估所有可能输入组合产生的噪声估计值，进而有效地选择产生噪声最小的输入因子组合作为后续构建模型的输入项。考虑到流域内点降雨变量数目众多，且以一对一的相关系数统计分析无法全面挖掘出各类模型输入变量组合的相关强度，而运用Gamma Test则可有效地找出最适合推估降雨-径流映射的因子组合。Gamma Test基本原理和计算步骤，详见文献 [11] [12] 。

2.2. 静态与动态神经网络

向后传播神经网络的架构为多层感知器，常使用的学习演算法为误差倒传播演算法，采用这样的组合的神经网络称之为倒传播神经网络(BPNN)。向后传播神经网络属于多层前馈式网络，以监督式学习方式来处理输入输出间的非线性映射关系，倒传播神经网络实现了多层神经网络的构想，为搜寻网络层中大量连结权重值提供了一类有效可行策略，为使用最为广泛的静态神经网络之一。

非线性自回归外因输入模式(NARX)，由Leontaritis和Billings于1985年提出，其回馈项是由输出层神经元的输出向量回馈到输入层的输入向量 [13] 。NARX同样采用监督式学习与误差倒传播演算法来进行网络权重修正与优化。在网络训练阶段，利用当前t时刻信息预报 $\hat{Y}\left(t+n\right)$ 时刻流量，其中对 $t+1,t+2,t+3,\cdots ,t+n-1$ 预测阶段目标值(真实值)无法获取，则将 $t+1,t+2,t+3,\cdots ,t+n-1$ 时刻模拟值 $\left(\hat{Y}\left(t+1\right),\hat{Y}\left(t+2\right),\hat{Y}\left(t+3\right),\cdots ,\hat{Y}\left(t+n-1\right)\right)$ 透过网络回馈作为NARX模式的输入项，用于预测t + n时刻流量 $\hat{Y}\left(t+n\right)$ 。

2.3. 长短期记忆神经网络(LSTM)

为解决NARX动态神经网络在深度学习过程(隐含层数 ≥ 2层)中引发的梯度爆炸和梯度消失问题，LSTM长短期记忆神经网络 [14] (如图1(b)所示)通过在NARX (如图1(a)所示)神经网络的隐藏层(Hidden layer)中引入存储单元(Memory cell)，即输入门(Input gate)、忘记门(Forget gate)、内部回馈连结(Self-recurrent connection)、和输出门(Output gate)来选择记忆当前信息或遗忘过去记忆信息(如降雨-径流映射关系)，以增强NARX神经网络的长期记忆能力。简而言之，LSTM长短期记忆神经网络是将NARX动态神经网络中的每个隐藏层换成了具有记忆功能的存储单元(Memory cell，如图1(c)所示)，简称LSTM cell，而其输入层(Input layer)和输出层(Output layer)与NARX动态神经网络相同。

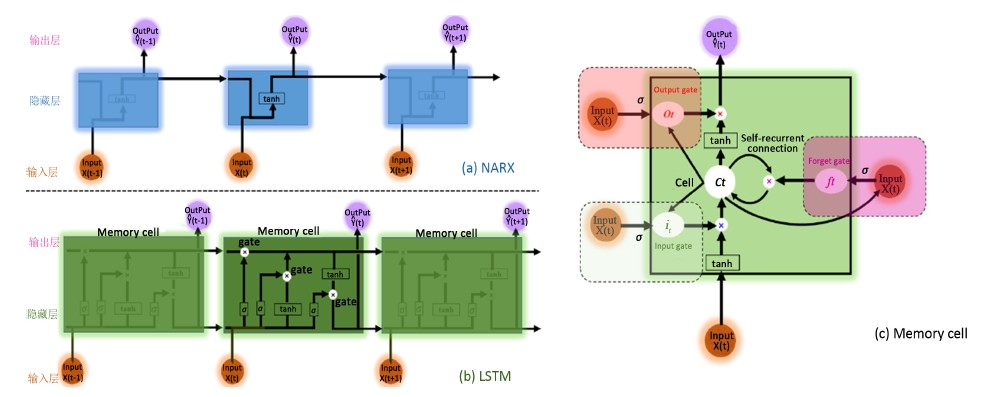
Figure 1. Comparison analysis between NARX and LSTM neural network architectures

图1. NARX与LSTM神经网络的架构对比图

标准的LSTM模型同样为三层神经网络架构，每一层的原理及公式分别描述如下。

1) Layer 1：记忆输入层(Input layer)

记忆输入层用于产生新记忆，通过使用当前信息 $X_t$ 和过去隐藏层状态 $h_{t-1}$ 来产生新记忆 ${\tilde{C}}_{t-1}$ 。

${\tilde{C}}_{t-1}=\tanh \left(W_c{X}_t+U_c{h}_{t-1}+b_c\right)$ (1)

式中： ${\tilde{C}}_{t-1}$ 为记忆输入层t − 1时刻产生的新记忆， $X_t$ 为当前t时刻的记忆输入信息， $h_{t-1}$ 为t − 1时刻隐藏层状态， $\text{tanh}(·)$ 为正切S形曲线激活函数， $W_c$ 为当前信息的权重系数， $U_c$ 为隐藏层状态的权重系数， $b_c$ 为记忆输入层的偏置系数。

2) Layer 2：隐藏层(Hidden layer)

① 输入门(Input gate)：在产生新记忆之前，网络需要判定当前信息 $X_t$ 重不重要，并做出是否记忆当前某些信息的决策。输入门根据输入信息和过去隐藏层状态 $h_{t-1}$ 共同判定记忆输入值是否值得保留，从而判定它以何种程度参与新的记忆。因此，它可以作为当前信息更新的一个评估指标。

$i_t=\sigma \left(W_i{X}_t+U_i{h}_{t-1}+b_i\right)$ (2)

式中： $i_t$ 为输入门t时刻的评估指标， $\sigma (·)$ 为Sigmoid激活函数， $W_i$ 为输入门中当前信息的权重系数， $U_i$ 为输入门中隐藏层状态的权重系数， $b_i$ 为输入门的偏置系数。

② 忘记门(Forget gate)：这个门和输入门类似，但它不能决定当前输入信息是否有效，仅对过去记忆单元信息做出评估，评估出是否选择忘记过去某些信息。因此，它可以作为过去记忆单元信息的一个评估指标。

$f_t=\sigma \left(W_f{X}_t+U_f{h}_{t-1}+b_f\right)$ (3)

式中： $f_t$ 为忘记门t时刻的评估指标， $\sigma (·)$ 为Sigmoid激活函数， $W_f$ 为忘记门中过去记忆单元的权重系数， $U_f$ 为忘记门中隐藏层状态的权重系数， $b_f$ 为忘记门的偏置系数。

③ 内部回馈连结(Self-recurrent connection)：回馈连结会根据遗忘门 $f_t$ 的评估结果，合理地选择忘记部分过去的记忆，再根据输入门 $i_t$ 的评估结果，产生新记忆 $C_{t-1}$ 。内部回馈连结可将过去和当前的记忆信息合并后产生新记忆 $C_t$ 。

$C_t=i_t\ast {\tilde{C}}_t+f_t\ast C_{t-1}$ (4)

式中： $C_t$ 和 $C_{t-1}$ 为内部回馈连结t和t − 1时刻的新记忆。

④ 输出门(Output gate)：它的目的是从隐藏层状态分离最终的记忆。最终记忆 $C_t$ 包含了大量不需要保存在隐藏层状态 $h_t$ 的信息，这个门能够评估出关于记忆 $C_t$ 哪些部分需要显示在隐藏层状态 $h_t$ 中。用于评估这部分信息的中间信号叫做 $o_t$ ，它和 $\tanh \left(C_t\right)$ 的乘积组成了最后的隐藏层状态 $h_t$ 。

$o_t=\sigma \left(W_o{X}_t+U_o{h}_{t-1}+V_o{C}_t+b_o\right)$ (5a)

$h_t=o_t\ast \tanh \left(C_t\right)$ (5b)

式中： $o_t$ 为输出门t时刻的中间信号， $h_t$ 为t时刻隐藏层状态， $$ 为输出门中当前信息的权重系数， $U_o$ 为输出门中隐藏层状态的权重系数， $V_o$ 为输出门中新记忆的权重系数， $b_o$ 为输出门的偏置系数。

3) Layer 3：输出层(Output layer)

与常规的RNN神经网络类似，LSTM输出层为隐藏层状态的总和输出。

$\hat{Y}\left(t\right)=W_y{h}_t+b_y$ (6)

式中： $\hat{Y}\left(t\right)$ 为LSTM神经网络t时刻的输出， $W_y$ 和 $b_y$ 分别为输出层中隐藏层状态的权重系数和偏置系数。

2.4. 机器学习算法

机器学习算法通过1) 降低深度学习网络的计算成本、2) 对网络层的参数添加惩罚项、3) 修改神经网络的结构(全连结变为非全连结网络)来解决循环神经网络(RNN)神经网络在深度学习过程中引发的梯度爆炸和梯度消失问题，防止RNN神经网络模型出现过拟合现象 [9] 。常用的机器学习算法有最小批量梯度下降法、正则化、筛选神经元等。各类机器学习算法分别描述如下。

1) 最小批量梯度下降法

梯度下降法是机器学习中最重要的优化算法之一，其更新神经网络参数时常采用以下两种方式。第一种，线下学习梯度坡降法，该方法采取遍历全部数据集算一次损失函数，然后算损失函数对各个参数的梯度，更新梯度。这种方法每更新一次参数都要把数据集里的所有样本都看一遍，计算量开销大，计算速度慢。第二种，线上学习梯度坡降法，该方法则采取每看一个数据就算一下损失函数，然后求梯度更新参数，虽然这个方法速度比较快，但是收敛性能不太好。为了克服上述两种方法的缺点，可采用最小批量梯度下降法，这种方法把数据分为若干批，按批来更新参数，由一批中的数据共同决定了本次梯度的方向，下降起来就不容易跑偏，减少了随机性。另一方面因为批的样本数与整个数据集相比小了很多，计算量也不大，可有效降低学习过程的计算时间成本。

2) 正则化

正则化是另一类有效防止模型过拟合的方法，正则项在优化过程中对网络层的参数(如权重系数)添加惩罚项，这些惩罚项将与损失函数一起作为网络的最终优化目标。常用的L2正则化操作的损失函数如下。

$L=L_0+\frac{\lambda }{2N}{\displaystyle {\sum }_{j=1}^N{w}_j^2}$ (7)

式中：L和 $L_0$ 分别为正则化后和原始的损失函数，后面一项即为L2正则化项，它为所有权重系数w的平方和，并除以训练集的样本容量N。 $\lambda$ 是正则项系数(为正值)，用于权衡正则项与 $L_0$ 项的比重。系数1/2则为了后面求导的计算方便，将求导后产生的2与1/2相乘刚好凑整。

梯度下降方向为通过对损失函数的网络层参数，即权重系数w和偏置系数b求导数，计算如下。

$\frac{\partial L}{\partial w}=\frac{\partial L_0}{\partial w}+\frac{\lambda }{N}w$ (8a)

$\frac{\partial L}{\partial b}=\frac{\partial L_0}{\partial b}$ (8b)

式中：w和b为网络层的权重系数和偏置系数。

可以发现L2正则化项对偏置系数b的更新没有影响，但是对权重系数w的更新有影响：

$w\to w-\eta \left(\frac{\partial L_0}{\partial w}+\frac{\lambda }{N}w\right)$ (9a)

$w-\eta \left(\frac{\partial L_0}{\partial w}+\frac{\lambda }{N}w\right)=\left(1-\eta \frac{\lambda }{N}\right)w-\eta \frac{\partial L_0}{\partial w}$ (9b)

式中： $\eta$ 为梯度下降法的学习速率参数(为正值)。

在不使用L2正则化时，求导结果中w前系数为1，现在w前面系数为 $\left(1-\eta \frac{\lambda }{N}\right)$ ，因为 $\eta$ 、 $\lambda$ 、N都是正数，所以 $\left(1-\eta \frac{\lambda }{N}\right)$ 小于1，它的效果是减小w，这也就是权重衰减的由来。依据奥卡姆剃刀定律，更小的权值w，表示神经网络的复杂度更低，对数据的拟合刚刚好，进而可有效的防止数据驱动模型的过拟合现象。

3) 筛选神经元

筛选神经元的基本原理：在保持神经网络模型的输入层和输出层不变的前提下，首先采用全连结(所有神经元参与训练)和BPTT算法训练一次神经网络模型，然后按一定比例(如50%)随机地“删除”隐藏层神经元，并采用非全连结(部分神经元参与训练)和BPTT学习算法更新神经网络中的权重参数。以上就是基于筛选神经元的一次迭代过程，在第二次迭代中，也用同样的方法，只不过这次删除一定比例的隐藏层神经元，跟上一次删除掉的可能是不一样的，因为我们每一次迭代都是“随机”删除，直至训练结束(达到最大迭代次数)。因此，筛选神经元可实现类神经网络的训练学习发展从全连结阶段迈向非全连结阶段，为分析数据驱动模型结构的不确定性提供了一种有效方法。

综上所述，三类神经网络的主要区别包括：1) 网络架构：BPNN属于无回馈机制的静态神经网络，NARX和LSTM均属于具有回馈机制的动态神经网络；2) 隐含层数：BPNN和NARX隐含层数为1层，而LSTM为深度学习网络，隐含层数 ≥ 1层；3) 记忆性能：BPNN具有良好的长期记忆性能，NARX具有良好的短期记忆性能，而LSTM具有较好的长期与短期相结合的记忆性能；4) 学习算法：BPNN和NARX采用线下学习梯度坡降法来优化网络学习过程，而LSTM则通过机器学习算法(最小批量梯度坡降法、正则化和筛选神经元)来优化网络学习过程。

2.5. 水文预报的评估指标

通常以评估指标值来衡量一个模型是否准确，或是比较不同模型的优劣。评估指标也常被用于模型的目标函数，如均方差(MSE)为修正神经网络模型参数或网络权重的常用指标。结合我国现行《水文情报预报规范》 (GBT 22482-2008) [15] 推荐使用的评价指标，采用以下评估指标对水文预报模型精度进行评定。

1) 合格率(Reliability, R)

流量预报以预见期内流量相对预报误差等于20%作为许可误差《水文情报预报规范》 (GB/T22482-2008)。一次预报的误差小于许可误差时，为合格预报。合格预报次数与预报总次数之比的百分数为合格率或可靠性，表示多次预报总体的精度水平。

$R=\frac{{\displaystyle {\sum }_{t=1}^N{m}_t}}{N}\times 100\%$ (10a)

$m_t=\{\begin{array}{l}1,\text{if}\left(R{E}_t\le 20\%\right)\\ 0,\text{else}\end{array}$ (10b)

$R{E}_t=\frac{\left|Y_f\left(t\right)-Y_o\left(t\right)\right|}{Y_o\left(t\right)}\times 100\%$ (10c)

式中： $Y_o\left(t\right)$ 和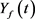分别为t时刻的实测流量和预报流量， $m_t$ 为合格预报次数，N为资料总时段数， $R{E}_t$ 为t时刻的相对预报误差。

2) 洪峰相对误差(Relative Error of peak, RE_p)

RE_p值若大于0则代表模型洪峰预报值偏小，若小于0则代表洪峰预报值偏大，若等于0则代表无预报误差。

$R{E}_p=\frac{Y_p-{\hat{Y}}_p}{Y_p}\times 100\%$ (11)

式中： $Y_p$ 和 ${\hat{Y}}_p$ 分别为场次洪水的洪峰实测值和预报值。

3) 均方根误差(Root Mean Squared Error, RMSE)

RMSE值越小表示模式的精度越高，尤其在评估具有较多中高数值时，RMSE较能体现模型的优劣。

$\text{RMSE}=\sqrt{\frac{1}{N}{\displaystyle {\sum }_{t=1}^N{\left(Y_f\left(t\right)-Y_o\left(t\right)\right)}^2}},\text{RMSE}\ge 0$ (12)

4) 基准拟合度G_bench (Goodness of fit with respect to benchmark, G_bench)

G_bench值若等于或小于0则代表模型与基准序列(Benchmark series)效用相同或较差，建议该模型不值得采用；若大于0则代表模型的效能较基本序列好；G_bench值越接近1表示模型效用越好。

$G_{\text{bench}}=1-\frac{{{\displaystyle \sum }}_{t=1}^N{\left(Y_f\left(t\right)-Y_o\left(t\right)\right)}^2}{{{\displaystyle \sum }}_{t=1}^N{\left(Y_o\left(t\right)-Y_{\text{bench}}\left(t\right)\right)}^2},G_{\text{bench}}\le 1$ (13)

式中： $Y_{\text{bench}}\left(t\right)$ 为带有时滞因子的基准序列。如采用 $Y\left(t-1\right)$ 流量序列预报 $Y\left(t\right)$ 或 $Y\left(t+1\right)$ 或 $Y\left(t+2\right)$ 流量时， $Y\left(t-1\right)$ 流量序列即为基准序列。

3. 实例研究

以长江上游的向家坝~三峡梯级水库区间流域为研究实例。向家坝水电站位于云南水富与四川省交界的金沙江下游河段上，坝址控制流域面积45.88万km²，占金沙江流域面积的97%。三峡工程位于宜昌市三斗坪，控制流域面积约100万km²，占长江全流域面积的55%以上。向家坝与三峡坝址之间的干流长度约为1140 km，其间汇入的支流主要有岷江、嘉陵江、沱江、横江、南广河、赤水、綦江和乌江。向家坝~三峡水库未控区间面积为9.26万km²，约占三峡控制流域面积的9.26%，流域水系图及水文气象站分布如图2所示。向家坝~三峡水库区间流域相关的气象水文资料数据(2003~2016年汛期6月~9月，6 h时间步长)，主要包括：1) 长江向家坝~三峡支流河段控制水文站的流量数据；2) 向家坝~三峡区间的67个地面雨量站长系列降水量数据，其中区间I面雨量为向家坝至寸滩水文站断面之间13个点雨量加权平均值，区间II面雨量为寸滩水文站断面至三峡水库断面之间54个点雨量加权平均值；3) 向家坝水库2013~2016年出库流量数据，由于向家坝水库2013年开始运行，2003~2012年流量由屏山站流量替代；4) 三峡水库2003~2016年入库流量数据。

Figure 2. Sketch maps and key elements in study area

图2. 研究区域要素示意图

3.1. 数据输入的优选结果

洪水传播时间因受流量大小和降雨强度等因素影响，干支流水库、水文站流量和区间雨量站传播至三峡水库时间为6~48 h不等。为有效地选择产生噪声最小的输入因子组合作为后续构建模型的输入项，表1给出了预报三峡水库t时刻流量Q(t)，其模型数据输入的Gamma test分析结果。据表1可知：1) 根据洪水传播时间可知，模型输入因子的可能组合为32 (=2 × 2 × 2 × 2 × 2)；2) 模型输入的最优组合的Ratio值为0.0005，代表该组合为32个可能组合中噪声误差最小，当输入组合的Ratio值为0.0259，代表该组合噪声误差较大，会因预报误差的传递，引起模型预报结果不确定性大。

Table 1. Results of optimal input combination

表1. 数据输入组合的优选结果

注：a) Q_o(t − 8)为测站具有48 h时滞(8 × 6 h)的实测流量。b) R_o(t − 6)为具有36 h时滞(6 × 6 h)区间面雨量。

3.2. 水文预报精度分析

将2003~2016年降雨–流量资料，划分为训练期(2003~2011年，4392个6 h时段资料)和测试期(2012~2016，2440个6 h时段资料)，其中训练期和测试期的最大洪峰流量分别为2010年7月20日02时68,300 m³/s和2012年7月25日02时69,100 m³/s。表2给出了各神经网络模型参数的初始设置和最优组合结果。据表2可知，BPNN、NARX、LSTM的参数组合数分别为16 (=1 × 16 × 1)、16 (=1 × 16 × 1)、500 (=1 × 1 × 10 × 10 × 1 × 5)。经过循环迭代计算，得出BPNN和NARX最优神经元个数分别为12和10，LSTM的最优参数结果分别为神经元数8、隐含层数3、最小批量学习长度40、筛选神经元概率0.4。

Table 2. Setting parameters in neural network models

表2. 神经网络模型参数设置

注：*5:1:20分别代表最小值、步长、最大值。Epoch为迭代次数，每迭代一次代表把数据集里的所有样本都计算了一遍。^#8 = 20 × 0.4，为初始神经元数(20) × 最优筛选神经元概率(0.4)。

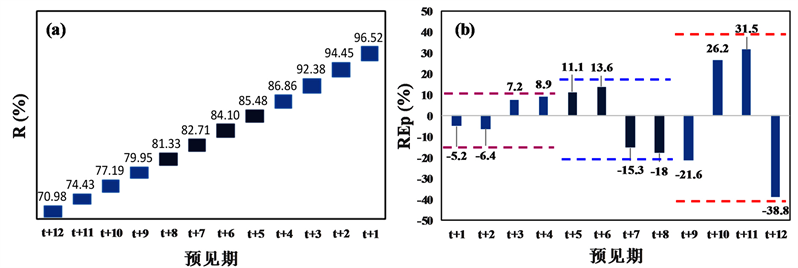
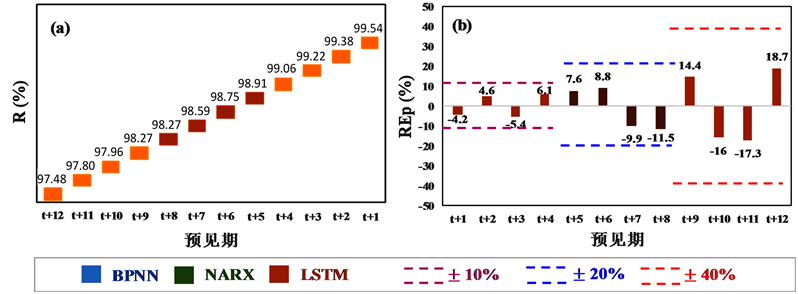
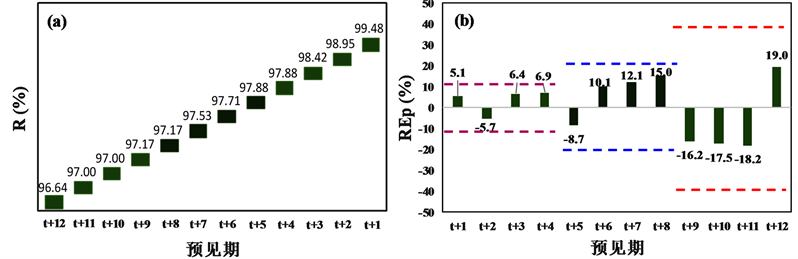
Figure 3. Reliability and relative error of peak discharge during testing period

图3. 测试期预报合格率(R)和洪峰相对误差(REp)结果

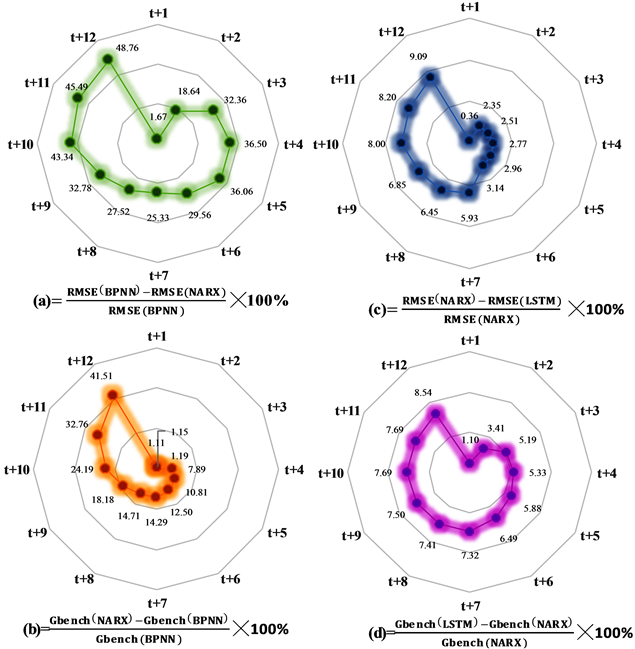
Figure 4. Root mean square error and goodness of fit during testing period

图4. 测试期均方根误差(RMSE)和基准拟合度模型(Gbench)结果

图3为对应最优参数组合时测试期预报合格率(R)和洪峰相对误差(RE_p)评价指标结果。从图3(a)合格率(R)指标分析：1) 1 d预见期(t + 1~t + 4)BPNN、NARX、LSTM模型精度均相对较高，预报精度均达到了我国现行《水文情报预报规范》(GB/T22482-2008)评定的甲等( $85\%<R\le 100\%$ )。2) 2~3 d预见期(t + 5~t + 12)具有回馈机制的NARX和LSTM动态模型精度显著高于无回馈机制的BPNN静态模型精度，其中NARX和LSTM模型预报精度均达到了甲等，BPNN模型预报精度达到了乙等( $70\%<R\le 85\%$ )。

从图3(b)洪峰相对误差(RE_p)指标分析：1) 1 d预见期(t + 1~t + 4) BPNN、NARX、LSTM模型精度均相对较高，RE_p位于区间范围[−10%, 10%]。2) 2~3 d预见期(t + 5~t + 12)具有回馈机制的NARX和LSTM动态神经网络模型精度显著高于无回馈机制的BPNN静态模型精度，其中NARX和LSTM的RE_p均位于区间范围[−20%, 20%]，而BPNN模型2d预见期(t + 5~t + 8)的RE_p位于区间范围[−20%, 20%]、3d预见期(t + 9~t + 12)的RE_p位于区间范围[−40%, 40%]。

图4为对应最优参数组合时测试期均方根误差(RMSE)和基准拟合度(G_bench)评价指标的对比结果。据图4可知，NARX相比BPNN，1 d预见期(t + 1~t + 4)的评价指标RMSE减幅为25%~49%，G_bench增幅10%~42%；LSTM相比NARX，1 d预见期的评价指标RMSE减幅为2%~9%，G_bench增幅5%~8%。2~3 d预见期(t + 5~t + 12)的评价指标RMSE减幅为25%~49%、，G_bench增幅10%~42%；LSTM相比NARX，2~3 d预见期的评价指标RMSE减幅为2%~9%、，G_bench增幅5%~8%。

4. 结论

降雨–洪水过程统计特征的非线性、随机性和时变性现象在变化环境的影响下愈发显著，而传统的静态和动态神经网络，无法有效地模拟这类统计特性。因此，如何适应变化环境及实现智慧水文预报，是水文科学研究领域极具挑战性的技术难题之一。本文提出了长短期记忆神经网络与批量学习、正则化、筛选神经元技术相结合的深度学习网络，构建了LSTM长短期记忆神经网络，并应用于三峡水库入库洪水预报。

从预报合格率、洪峰相对误差、均方根误差和基准拟合度四个指标综合评估可知，相比BPNN静态神经网络和NARX动态神经网络，LSTM长短期记忆神经网络结合三种深度学习的辅助算法，有效提高了三峡水库入库洪水的预报精度。LSTM长短期记忆神经网络可以有效地防止深度学习神经网络的过参数化和过度拟合技术瓶颈，提高了数据驱动模型的预测精度、具有良好的稳健性及泛化能力。

基金项目

国家重点研发计划(2018YFC0407904)和中国博士后科学基金项目(2017M620336)资助。