1. 引言
雷达目标检测是一个典型的二元假设检验问题,需要从分辨单元接收到的雷达回波序列构造检测统计量,同时设置检测阈值,如果检测统计量大于或等于设定的检测阈值,则判定该分辨单元内存在目标;反之则判定该分辨单元不存在目标 [2]。
雷达距离分辨率单元的大小与发射信号带宽成反比,因此宽带雷达具有更高的距离分辨率。距离分辨单元的减小使得每个距离单元中杂波的后向散射功率也随之降低,但是对于目标而言,其强散射中心的尺寸通常小于雷达的一个距离分辨单元,因此相比于传统的窄带雷达,宽带雷达回波具有更高的信杂比,改善了雷达在杂波中检测目标的能力 [3]。
目前,针对威布尔分布下的距离扩展目标的检测问题,传统的检测器有能量检测器、M/N二进制检测器等。其中能量积累检测器在杂波分布偏离高斯分布时检测性能迅速下降,则威布尔分布杂波模型下的目标检测性能下降。M/N二进制检测器基本思想是:首先选出回波幅度超过第一门限的单元,如果在一定距离段内这样的单元数目超过第二门限,则判定该距离段内存在目标 [4]。M/N二进制检测器的性能由两个门限共同决定。而M/N二进制检测器由于采用了复杂的变换使检测量的概率密度函数变得极其复杂,检测门限不易得到。本文将通过构造新的检测量来求解威布尔分布下目标的检测问题,解决能量检测器在威布尔杂波情况下的性能问题及M/N二进制检测器的计算复杂的问题,最后证明本算法的有效性。
2. 基于矩估计的参数估计
常用的参数估计方法有矩估计法和极大似然估计,考虑到矩估计法计算的方便性,利于实时检测,本文将采用矩估计法来估计威布尔分布的两个参数值。
矩估计法(estimation by the method of mo-menu)又称为数字特征法。以样本矩的某一函数代替总体矩的同一函数来构造估计量的方法称为矩估计法 [5]。因为样本可确定一个经验分布函数,由这个经验分布函数可确定样本各阶矩。而样本又是从总体中随机抽取而来,样本的分布及其各阶矩都在一定程度上反映着总体参数的特征,当样本容量n趋于无限大时,样本矩与相应的总体矩任意接近的概率趋于1,因而可用样本矩代替总体矩构造一个含有未知参数的方程或方程组,方程的解就给出总体参数的估计量 [6]。
假设连续型随机变量X的概率密度函数为
,或者离散型随机变量X的分布律为
,其中
为概率密度函数的待估参数,
是来自X的样本。假设样本X的前m阶矩存在。
,X连续 (1)
或
,X离散(2)
在通常情况下,它们是
的函数。在矩估计中,我们基于以下假设,样本矩
(3)
收敛于总体矩
,样本矩的连续函数收敛于总体矩的连续函数,这样,就可以以样本矩来作为总体矩的一个估计,把样本矩的连续函数作为总体矩连续函数的一个估计 [7]。具体步骤为
(4)
这是一个由k个方程组成的方程组,每个方程包含k个未知参数
,一般情况下,可以求解出一组唯一的解
。以
代替上式中的
,可以计算出一组
,将
作为
的估计量,这种估计量称为矩估计量。矩估计量的观察值为矩估计值。设X为连续型随机变量,其m阶原点矩为
,
是来自X的样本。其m阶原点矩为
(5)
在矩估计中有
(6)
威布尔分布服从的概率密度函数为
(7)
威布尔分布函数为
(8)
其中
是尺度参数,表示分布的强度;
是形状参数,表示分布的偏斜度 [8]。
概率密度函数为威布尔分布随机变量的m阶原点矩为
(9)
由式(9)得
(10)
解方程(10)可得到威布尔分布的参数估计。
求解方程式(10)得到
(11)
3. 威布尔分布的非相干积累
设
为N个杂波样本且独立同分布,经非相干积累后随机变量
的PDF为
,
的矩母函数为
(12)
当随机变量
服从威布尔分布时,
(13)
当各阶矩存在的随机变量,不管是离散型的还是连续型的都可以定义矩母函数
,(14)
则结合式(9),式(14)可写成
(15)
的矩母函数为
(16)
上式经过拉普拉斯反变换可得到随机变量
的概率密度函数
[9] ,但是
无法以闭合形式给出解析式。所以直接对威布尔分布进行非相干积累没有办法获取非相干积累后的概率分布,无法将其应用到目标检测的问题中去。
4. 算法设计
4.1. 问题描述
对宽带雷达体制,目标回波信号延展到多个距离分辨单元,形成距离像。为研究方便,作如下假设:
为距离波门内的采样信号,每个距离分辨单元采样1个点,目标距离像的起始和终止位置分别为
和
,L为目标强散射点所占据的距离分辨单元个数,称之为距离像长度 [10]。
设雷达系统对回波的采样点数为L。在每一个距离单元上,观测量表示为
,目标回波量表示为
,假定
服从自由度为2m (m是自然数)的
分布,其概率分布函数为
,
(17)
 是威布尔分布,表示背景杂波,这里采用两步法,先假设杂波参数
已知,再通过背景杂波进行估计得到。设目标回波的距离像分布不超过L个距离单元,对检测窗内的数据建立如下检测模型:
是威布尔分布,表示背景杂波,这里采用两步法,先假设杂波参数
已知,再通过背景杂波进行估计得到。设目标回波的距离像分布不超过L个距离单元,对检测窗内的数据建立如下检测模型:
(18)
4.2. 似然比检验
NP 准则下,假设检验式(16)的最优检测器为似然比检测器 [11] (Likelihood Ratio Test, LRT),其表达式为:
(19)
其中
是
在
假设下的PDF,
是
在
假设下的PDF,
是相应的检测门限。适当的变换有时候可以很大程度地简化实际LRT计算量,通常的做法是对式(19)两边取对数,得到对数似然比
(20)
其中
。
式(20)可以作为威布尔分布的最优检测器,但是却无法直接应用于工程中。
在
假设下,有
(21)
在
假设下,有
 (22)
(22)
由式(21)、(22)可知,求解
比较复杂,另外,其虚警率对应的门限也需要用蒙泰卡罗方法求解,不适于工程应用。
4.3. 指数分布与
分布的关系
假设
独立同分布,且服从
,即服从指数分布。
当
时,
(23)
所以指数分布是
分布的一种特殊形式;
假设当
时,
服从
成立,当
时,
,其中 服从
,
服从
,
服从
,
服从
,
(24)
则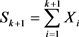 服从
分布。
服从
分布。
综上,多个独立且相同分布的指数分布变量的和服从Gamma分布。
4.4. 检测器设计
假设
条件下,
的概率密度函数表达式为:
(25)
将服从威布尔分布的雷达杂波
做如下变换:
(26)
推倒得到
(27)
将上式对
求导,得
的概率密度函数为
(28)
由式(28)可以看出
服从标准指数分布。
检测器构造如下检测量t:
(29)
在威布尔杂波下的检测策略为:
由4.3可知多个独立且相同分布的指数分布变量的和服从Gamma分布,由因为
服从标准指数分布,则
服从
分布,则
(30)
其中
为
分布的概率密度函数。由式(30)求出检测门限T,与检测单元计算得到的t比较,即可得到检测结果。
检测流程:
1) 根据参考单元估计出威布尔分布的两个参数值;
2) 通过式(30)计算出门限值T;
3) 通过式(26)对检测单元进行变换;
4) 通过式(29)计算检测统计量t的值,将该值与门限值T进行比较得到结果。
5. 威布尔分布与指数分布仿真
在4.4节中通过公式推导证明威布尔分布通过
变换后变成标准指数分布,在本节中将仿真4组威布尔分布,
与
随机取值,通过仿真来证明威布尔分布可以通过变换变成标准指数分布,标准指数分布与威布尔变换后分布的PDF曲线如图1所示。

Figure 1. PDF curve of standard exponential distribution and distribution after Weibull transformation
图1. 标准指数分布与威布尔变换后分布的PDF曲线
其中虚线代表理论上的标准指数PDF曲线,实线代表威布尔分布通过
变换后的PDF曲线,二者非常相近。
6. 算法仿真
6.1. 算法的稳定性
仿真场景:当威布尔分布描述一些典型的海杂波时形状参数
的值多分布在1到2之间,尺度参数
不做要求 [12] ,所以在仿真时威布尔杂波的尺度参数
取2.2和形状参数
取1.5,虚警率
设置为10−3,蒙特卡洛仿真次数
,目标占据20个距离单元,目标回波服从卡方分布,信噪比SNR从−5 dB逐步增加到10 dB,仿真尺度参数
和形状参数
的不同估计值情况下的检测情况。
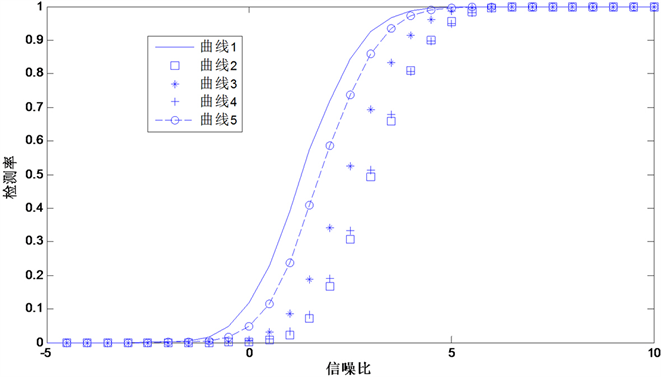
Figure 2. Detection curve under different estimation conditions
图2. 不同估计情况下的检测曲线
图2中曲线1为参数估计准确时的检测结果曲线,曲线2和曲线3分别为尺度参数
估计值比准确值小5%、大5%时的检测结果曲线,曲线4和曲线5分别为尺度参数
估计值比准确值小10%、大10%时的检测结果曲线,其中形状参数
的取值方法为:仿真10000组相关威布尔分布的样本,每组样本包含200个数据,尺度参数
为2.2和形状参数
为1.5,通过矩估计法得到威布尔分布的参数,在估计得到的10,000组参数中找到尺度参数估计值比准确值小5%、大5%、小10%、大10%的4组估计值,对应的形状参数的估计值便可以得到。从图中可以看出,当参数估计准确时的检测结果最好,当参数估计存在偏差时,检测率并没有下降很多,可以看出本算法具有良好的稳定性。
6.2. 检测率仿真
仿真场景:威布尔杂波的尺度参数
为2.2和形状参数
为1.5,虚警率
设置为10−3,蒙特卡洛仿真次数
,目标占据20个距离单元,目标回波服从卡方分布,信噪比SNR从−5 dB逐步增加到10 dB,仿真本文提到的算法、二进制检测算法及能量检测算法,对比这三种检测算法。
图3中曲线1为本文的检测算法,曲线2为二进制检测算法,曲线3为能量检测算法,从图中可以本文提出的检测算法在信噪比相同的时候,比M/N二进制检测算法的检测率高,但是比能量检测算法的检测率低。
6.3. 虚警率仿真
仿真场景:威布尔杂波的尺度参数
为2.2和形状参数
为1.5,虚警率
设置为10-3,蒙特卡洛仿真次数
,目标占据20个距离单元,目标回波服从卡方分布,仿真只有杂波时,本文提到的算法、M/N二进制检测算法及能量检测算法的虚警率。
分别仿真三种算法,本文提到的算法虚警率为0.00041,M/N二进制检测算法为0.00062,均在设置
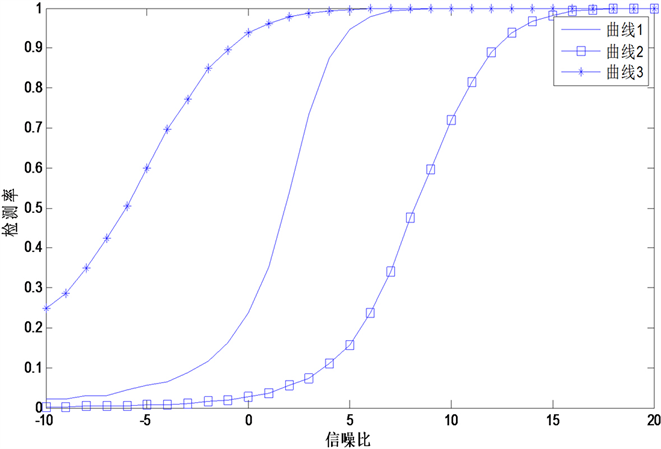
Figure 3. Detection rate simulation curve
图3. 检测率仿真曲线
的虚警率0.001以下,是恒虚警的,而能量检测算法的虚警率为0.00845,大于设置的虚警率。
综上,本文提出的算法和M/N二进制检测算法都具有恒虚警性质,但是本文提出的算法比M/N二进制检测算法的检测率高。虽然能量检测算法比本文提到的算法的检测率高,但是能量检测算法却是以牺牲恒虚警为代价来提高检测率。所以本文提出的检测算法比其他两种算法的检测性能都更优。
7. 结束语
本文研究了威布尔杂波模型下的扩展目标检测问题,针对传统检测算法存在的问题,如能量积累检测器在威布尔杂波下检测性能迅速下降,M/N二进制检测算法的一次虚警概率没有解析解且检测性能不理想等问题,另外,本文通过研究发现威布尔分布非相干积累没有解析解,且威布尔分布下的杂波检测的最优检测器也没有解析解,针对以上问题,本文提出一种新的检测量,将威布尔分布转换成标准指数分布,同时利用指数分布与Gamma分布的关系来获得检测阈值,使威布尔分布下扩展目标检测问题得到很大的简化,性能也明显的提升,且算法具有较好的稳定性。本算法属于参数化检测算法,使用该算法的前提是杂波分布的类型估计准确,若杂波分布估计错误,检测器的检测性能会下降,所以在下一步的研究中,拟重点研究非参数化检测算法,使算法具有更广的应用范围。