1. 引言
海洋内波是发生在海洋内部的波动 [1] 。在非线性和频散作用相平衡的情况下,其恢复力主要是重力与浮力的合力,常以内孤立波(Internal Solitary Wave)形式传播。内波的典型尺度为几米到百米左右,周期从几分钟到几天不等,典型的水平尺度从几米到数千米。海洋内波存在垂向波数 [2] ,根据内波控制方程,在其传播的深度范围内会有不同的内波模态。内波的垂向结构并不是单一的模态,是多个模态的组合结果,往往第一模态占主导,第二模态次之,第三、第四模态再次之。
内波的波长、波向等信息容易从SAR图像中获得 [3] [4] 。另外,近几年很多低纬度可见光图像中也发现了海洋内波现象,这种内波现象往往在可见光图像太阳耀斑区。可见光图像内波成像机理与SAR成像机理类似,都是由于内波区域海表的辐聚和辐散调制了海表粗糙度,从而引起SAR后向散射系数的不同或可见光反射强度的不同。
内波振幅信息一直是内波参数反演的难点,可以用KdV方程从SAR图像估计内波的相速度和振幅 [4] 。从SAR图像中得到内波基本参数的方法我们同样可以应用到可见光图像中。
本文基于可见光遥感图像反演内波波长、振幅、等内波特征参数,并将这些参数与海洋密度剖面资料相结合,并据此求解内波垂向特征函数的前三个模态,由于内波垂向模态中,第一模态占主导地位 [5] ,因此,可利用第一垂向模态函数,根据内波物理原理,通过数值的处理得到内波二维断面模型。内波垂向二维断面构造流程如图1所示。
内波垂向二维断面构造的步骤为:对输入的CCD图像进行处理,选取有内波存在的一个内波剖面,对剖面数据进行信号提取,通过适当的滤波后获取CCD图像中内波对信号起伏。此时,只能获取遥感CCD数据所反映的内波海表信息,若想得到内波在水下的振幅或内波水下波动信息,必须有该区域的垂向密度剖面信息作为辅助。通过内波控制方程,得到内波海表信号起伏与内部振动之间的关系,从而反演海洋密度跃层处内波在海洋内部的振动和起伏情况,再根据内波垂向模态函数反演得到海洋内部内波的波动,构造内波垂向结构。
2. 数据准备
从数据处理流程来看,可见光图像信号起伏信息、内波振幅、内波垂向模态函数是构造内波二维断面的三个要素。下面将详细描述这三个要素获取方法。
2.1. 内波剖面数据获取
CCD可见光遥感图像是内波特征参数振幅、波长等反演的基础,反射率可以反应海面散射特性,进而反应海面流场辐聚辐散规律,由于内波到达海面时振幅基本为0 [6] ,因此可通过信号剖面得到内波表面流场的分布规律,进而得到内波振幅在断面中的起伏规律。本文所用可见光数据是由中国资源卫星应用中心提供的HJ数据,获取时间为2010年7月2日,数据地理位置为
,
,经向分辨率为30.00 m,纬向分辨率为30.00 m,如图2所示。
选取左下角内波区域并尽量沿着与波锋线相垂直方向选取一个断面,此断面一定要尽量避开云区,具体如图3所示。
根据图像中选取的剖面位置,提取剖面信息,即根据图3中黑线线段覆盖部分的位置,可将图像根据线段距离进行插值,提取对应CCD图像中的可见光图像信号。选取的剖面数据及对其进行滤波平滑处理后结果如图4所示。

Figure 4. CCD data signal fluctuation
图4. 可见光数据信号起伏
2.2. 内波振幅
本文所用方法是陈维亮等提出的一种基于实测资料的内波振幅修正的方法 [7] 。利用这种方法反演得到温跃层处的内波振幅,在此不再赘述。
2.3. 内波垂向模态函数
内波控制方程整理简化后为如下形式:
(1)
式中:z是深度,
为浮力频率;
为内波圆频率;g是重力加速度;f为地转惯性频率;
为水平波数;
为内波垂向速度于深度的一阶导数,
为内波垂向速度于深度的二阶导数。
有了可见光数据和密度剖面数据后,通过反演内波波长、振幅、相速度,除
外,式(1)中的参数都可以计算出来。
本文根据内波尺度特点忽略地转影响,通过量级分析忽略系数较小的一阶微分项,将采用矩阵解法和刚盖近似对内波控制方程改写如下:
(2)
k为水平波数。令: 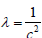 、
,则方程变为:
、
,则方程变为:
(3)
将整个海深
分成厚度均为
的
层。并令:
、
其中
。
将上式代入方程可得:
 (4)
(4)
其中
。
编程求解标准化方程,可计算得到各个模态的垂向特征函数。
垂向模态的求解需要背景场的垂向密度剖面数据,该数据可通过海上试验测量得到。但由于可见光图像内波区域离岸较远,很难获取可见光成像同步海上测量密度剖面数据。因此,本文中,利用WOA95平均场数据替代,该数据空间分辨率为
,时间分辨率为1个月。
根据可见光数据所在的经纬度位置估算内波区域位置,从WOA数据中提取当地背景场密度剖面数据。该数据水深约80 m,是一个常见浅海密度结构,垂向密度结构如图5所示。
根据2.1中提取的内波剖面,及内波波长、振幅提取方法,计算内波得到波长为512.5 m,振幅为25.2 m。
将内波波长信息代入式(4),求解得内波垂向模态函数,如图6所示为前三个模态。
3. 内波二维模型的构建
根据可见光图像的数据起伏和连续层化流体的稳定态内孤立波解构造可反演无量纲海洋内波波动起伏。在得到内波垂向振幅和垂向模态函数后,将三者结合起来可以计算内波垂向二维断面 [8] [9] 。
3.1. 垂向标准层振幅的构造
垂向模态函数中的数值大小能够反映内波位移的相对大小 [9] 。由于内波垂向模态中,第一模态为主导模态,为便于研究,本文采用第一模态函数来反映海洋垂向分布特征。
设温跃层所在深度为
,则本文中所述的振幅A实际上是温度跃层处的振幅,该振幅也是内波在海洋内部的最大振幅,若
表示第一模态函数每个分层模态函数值与温跃层处模态函数值的比值,则
即为按照垂向分层每层的振幅。

Figure 5. The density section in experiment
图5. 实验所用密度断面

Figure 6. Vertical mode functions in experiment
图6. 实验所得垂向模态函数
3.2. 垂向标准层无量纲波动起伏反演
根据KDV方程,连续层化流体的稳定态内孤立波解为:
 (5)
(5)
其中,
为内波位移,t为时间,x表示水平方向位置,
为内波振幅,
为内波半波宽度,
为内波相速度。
参考SAR成像机理,可见光图像内波流场太阳耀斑区内波亮度为:
(6)
当内波为下凹形内波时A是一个正常数,当内波为上凸形时,为负常数 [10] 。由内波遥感成像理论,如果跃层以上水深小于跃层以下水深,则内孤立波为下凹形内孤立波,反之,则为上凸型内波 [11] [12] 。下凹形内波在前导波的前部产生辐聚,而后部产生辐散。根据可见光内波成像机理,辐聚部分水表面更为粗糙,在可见光耀斑图像中表现为暗纹,因此在可见光图像中下凹形内孤立波的前端为暗条纹,后端为亮条纹,反之上凸型内部前端为亮条纹,后端为暗条纹。
根据式(5)和式(6)所示的内波振幅与可见光图像内波亮度的关系,可根据可见光图像信号起伏拟合得到无量纲内波振幅起伏,如图7所示。

Figure 7. Distribution of dimensionless internal waves along the section
图7. 沿剖线无量纲内波波动分布
3.3. 内波二维断面重构
设
为随位置变化的内波引起的海水位移,则有:
(7)
按照上述流程,即根据WOA背景剖面数据和模态函数反演的内波标准层垂向振幅分布、根据可见光图像剖线反演得到沿剖线(水平方向)无量纲内波波动分布,并结合WOA剖面数据可重构得到内波垂向结构,如图8所示。
图8(a)为内波垂向二维温度断面重构结果,图8(b)为内波垂向二维盐度断面重构结果,图8(c)为内波垂向二维密度断面重构结果。图像中横坐标为水平方向点数,纵坐标为水深。由图中也可以看出,由于采用第一模态构建而成,垂向波动只有一个波动极大值深度(温跃层处),从温跃层向上和向下内波波动都在减小,到达水面和海底时,振幅几乎为0。
4. 结论
本文通过可见光图像的数据信息,垂向模态函数以及内波振幅三者结合,根据内波形成和观测机理,对内波引起的温、盐、密分布进行了二维垂向剖面的重构。
采用上述方法进行内波区剖面的重构仍然存在一些需要改进的地方,主要体现为:
1) 在内波垂向模态函数的分解中,根据内波理论和以往测量经验获知第一模态是主导模态,但不可否认还有第二模态、第三模态等后续模态的存在。由于无法解得各个垂向模态函数在实际内波中所占的权重比例,本文只用第一模态函数重构内波二维断面,重构模型尚不够精细。若能用尽量多的垂向模态函数权重叠加来代表内波区的垂向分布结构,则重构结果将更接近实际。
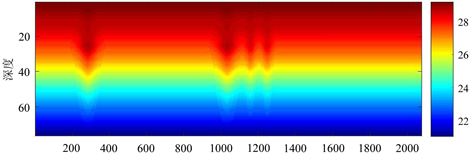 (a) 温度重构
(a) 温度重构  (b) 盐度重构
(b) 盐度重构  (c) 密度重构
(c) 密度重构
Figure 8. Vertical reconstruction of internal wave
图8. 内波垂向重构
2) 在内波垂向密度剖面提供方面,本文采用空间分辨率为
的月平均背景场获取内波发生处海水剖面数据,在时间和空间上都不够精确,若能同时获得当时当地的可见光数据,重构结果将更加符合实际。
基金项目
本论文由国家863军口项目,编号2015AA7014047基金支持,并由国防科技创新特区项目(17-163-16-XJ-014-005-01)项目支持。