1. 研究的问题
考虑如下的时间分数阶Fokker-Planck方程(FFPE):
(1.1)
初始条件和边值条件为
(1.2)
其中
,
为正常数,
为给定函数,方程(1.1)中的分数阶导数为Riemann-Liouville分数阶导数
,
是Gamma函数。方程(1.1)可用于模拟外力场作用下的低扩散现象(参见 [1] )。
对于方程(1.1)的求解,已有数值解法多数是针对f是常数或是x的函数情况(参见 [2] - [10] ):如对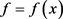 情形,Chen [5] 设计有限差分方法,Jiang [3] 针对Chen [5] 中的数值格式给出了稳定性和收敛性的证明;Vong [10] 设计了一种高阶差分格式并证明它的稳定性和收敛性。据我们所知,对于
情况,仅有Le [11] 研究了两种方法,第一种是时间上连续方法(在空间中使用分段线性Galerkin有限元方法),第二种是空间连续方法。
情形,Chen [5] 设计有限差分方法,Jiang [3] 针对Chen [5] 中的数值格式给出了稳定性和收敛性的证明;Vong [10] 设计了一种高阶差分格式并证明它的稳定性和收敛性。据我们所知,对于
情况,仅有Le [11] 研究了两种方法,第一种是时间上连续方法(在空间中使用分段线性Galerkin有限元方法),第二种是空间连续方法。
有限体积法已开始应用于求解分数阶方程,如 [12] 对空间分数阶方程采用了有限体积方法; [13] 利用有限体积方法数值求解时间–空间分数阶方程; [14] 对二维时间分数阶偏微分方程进行有限体积方法研究(其中
)。
本文设计求解(1.1)的有限体积法,其中空间导数使用中心差分格式进行离散,时间分数阶导数使用一阶线性多步法进行离散。数值实验结果表明该方法在时间上和空间上分别具有一阶和二阶收敛性。文中假定解u充分光滑,C网格大小无关的正常数。
2. 离散
在
上取分点为
,
,其中时间步长
,L为正整数。在区间
上取分点
,其中空间步长
,N为正整数。N个空间有限体为
,其中
。
在方程(1.1)中取
得到
(2.1)
利用向后差分,(2.1)式左侧可以写成
(2.2)
其中
满足
。
用Lubich一阶线性多步法逼近Riemann-Liouville分数阶导数(参考文献 [15] )
(2.3)
其中
,
满足
,
是与解u有关的光滑函数。
将(2.2)式,(2.3)式带入(2.1)式中,得
(2.4)
用
表示
的近似,由(2.4)我们得到原问题的时间半离散格式
(2.5)
记
(2.6)
易知
(2.7)
将(2.6)式,(2.7)式带入(2.5)式中,得到
(2.8)
在有限体
上对(2.8)式积分
(2.9)
利用中矩形积分公式,用
表示
,(2.9)式左侧可以写成
(2.10)
其中
(2.11)
用
表示
,(2.9)式右侧可以写成
(2.12)
用中心差分格式,(2.12)式右侧第一项可以写成
(2.13)
其中
(2.14)
由于(2.12)式右侧第二项可以写成
(2.15)
其中
(2.16)
将(2.10),(2.12),(2.13),(2.15)式带入(2.9)式中,得
,
(2.17)
用
近似
,由(2.17)式我们可以得到如下的有限体积法(FV):
,
(2.18)
初始条件和边值条件为
(2.19)
3. 数值实验
本节利用我们设计的有限体积法解决{(1.1)(1.2)}问题。考虑下列具有精确解的方程
(3.1)
初始条件和边值条件为
,其中
(3.2)

Table 1. Convergence rate for space with α = 0.2, L = 50,000
表1. 空间收敛阶α = 0.2,L = 50,000

Table 2. Convergence rate for space with α = 0.5, L = 50,000
表2. 空间收敛阶α = 0.5,L = 50,000

Table 3. Convergence rate for space with α = 0.8, L = 50,000
表3. 空间收敛阶α = 0.8,L = 50,000

Table 4. Convergence rate for time with α = 0.2, N = 5000
表4. 空间收敛阶α = 0.2,N = 5000

Table 5. Convergence rate for time α = 0.5, N = 5000
表5. 空间收敛阶α = 0.5,N = 5000

Table 6. Convergence rate for time with α = 0.8, N = 5000
表6. 空间收敛阶α = 0.8,N = 5000
。此方程的精确解为
。
我们定义空间和时间收敛阶如下:
空间收敛阶的数值结果列于表1~表3中,时间收敛阶的数值结果列于表4~表6中。数值实验表明该方法在时间和空间上皆为一阶收敛,当空间网格足够细时,空间上可以达到二阶收敛。
致谢
感谢我的导师姜英军教授和我的师兄周帅虎对我论文写作的悉心指导和热情帮助。
基金项目
国家自然科学基金(11571053)。